Following the logs

• 43. PAM3 and the bi-Trits
• 45. Constellation 2

Today's concern is about "optimising" a word's coding to reduce droop. There should be approximately as many -1 and +1 levels. This increases the number of bits per word but we have one possible bit:

Words (so far) are 20 bits wide, and symbols represent 3 bits, 3×7=21, so we could select one encoding among two... What could this bit affect ? It's not a XOR of the input bits since the constellation seems to be quite symmetrical and XORing the inputs would just flip the signal's polarity and nothing is solved.

Let's go back to the current constellation:

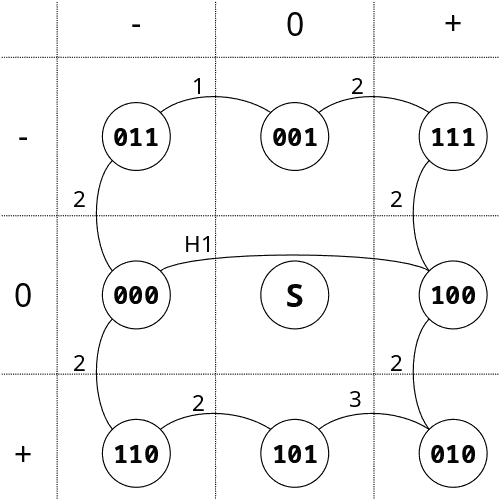
The corresponding tables:

encoding:
bits  trits
000    - 0
001    0 -
010    + +
011    - -  \
100    + 0  /
101    0 +
110    - +
111    + -

decoding:
trits   pos  neg
 - -    011  010
 - 0    000  100
 - +    110  111   <= requirement for polarity sense
 0 -    001  101
 0 +    101  101
 + -    111  110   <=
 + 0    100  000
 + +    010  011

As previously noted, the table is almost symmetrical, but not completely (and this is on purpose), so the polarity is handled at the output of the comparators, not at the table level.

• One possibility to affect the balance of output levels would be to "rotate" the constellation by 90°, as it would preserve the Hamming distances between consecutive codes. But then it amounts to the same thing as swapping the first and second trit, which does not change much of anything.

• The second possibility is to rotate by 45° (clockwise or anti, it's mostly the same overall, I think) so a second table is required. Expensive.

• The 3rd possibility would be to rotate the input bits of the table: one table, one weighing circuit (2×popcount), 6 input permutations... and several cycles to elect the best one, possibly also considering the past values, to reduce baseline wander. This is possible since it still operates rather "slowly" and there is no need to test all permutations in parallel.

6 permutations require a whole bitrit to encode, and 2 symbols are lost (out of 8 tribits).

• 4th possibility is to "increment" all the tribits and test 8 cycles => a whole bitrit is used. This would help in the cases were long strings of 0s or 1s are sent, or any 3-bit pattern.
• The balancing system should account for the "Same" symbol, which outputs 00 when the tribit is the same as the previous one.

.

Some of the permutations/increments should have some symmetries and could be discarded, I guess.

Each tribit is expanded to four bits, 2 pairs that represent one trit each, with the encoding

00 => 0
10  => +
01  => -

=> It is possible to replicate a popcount circuit for the droop estimate, 20 bits => 14 trits => 4 bits per polarity suffice and such a circuit has already been designed for the ParPop circuit. Well, the sum can vary from -14 to +14 so that's 5 bits total.

A pre-decoding table can be used, derived from the original encoding table.

encoding:
bits  trits  weight
000    - 0   -
001    0 -   -
010    + +   ++
011    - -   --
100    + 0   +
101    0 +   +
110    - +   0
111    + -   0

Nice, the LSB is almost unused. The 5 output codes need 3 bits, or 4 bits to encode them separately (-, +, -- and ++) to be processed by a less dense circuit.