The constellation has a nice property that has been already highlighted:

encoding:
bits  trits  weight
000    - 0   -  \____NOR2
001    0 -   -  /
010    + +   ++ ---NOR+AND
011    - -   -- ---ANDN+AND
100    + 0   +  \____ANDN
101    0 +   +  /
110    - +   0
111    + -   0

The net sum of the levels does not need a lot of gates to evaluate: the circuit takes about 4 gates.

Of course, let us not forget the activation/enable, coming from the circuit we have already designed in the last log 2. The "Same" circuit. Since 11x totals 0, then we can just OR the result on b2 and b1 as in the circuit below:

Now the goal is to evaluate the total bias of the encoded 20-bit word, for each of 8 "fumblings" of the 7 tribits. Initially I imagined an incrementer but there is much simpler than that: XOR each tribit with the output of a 3-bit counter. Then the winning count gets encoded with the others. The cost is one more layer of XOR2 at the input of the circuit:

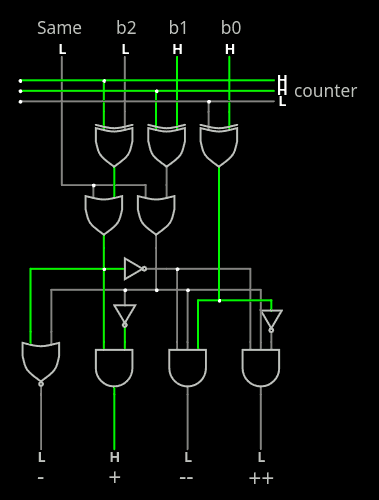
And from there we can simply add a popcount7 for each of the 7 outputs and combine them in a 32-bit "weight". But even though it's already "done", we can already simplify it a bit by noticing that neighbours can cancel each other. So let's introduce another new circuit: the reduction. To simplify it, I need to add a "zero" output to the bias decoder. And then, things took a weird turn. Here is the new circuit that combines 2 tribits:

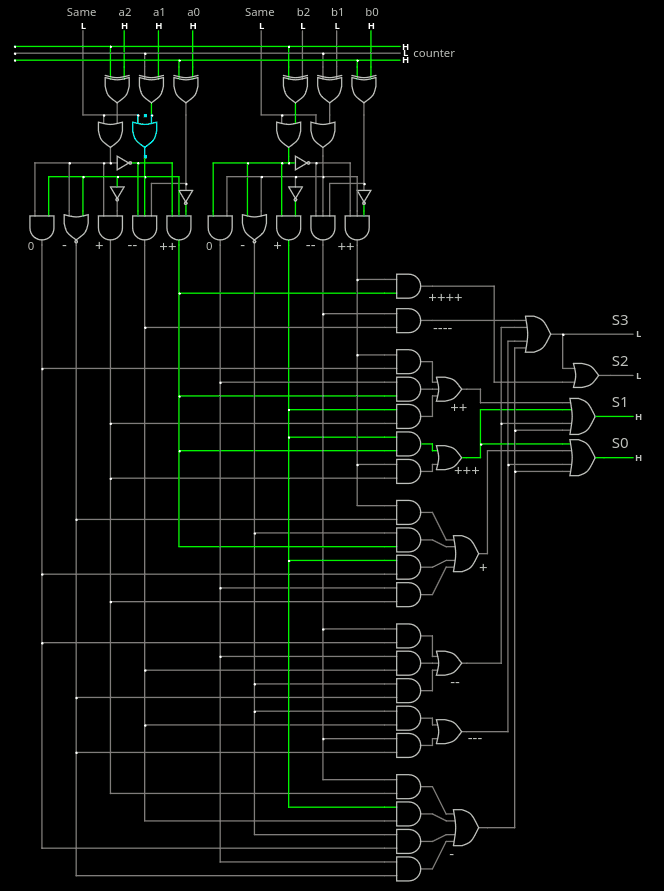
Now there is a big binary encoder and the 4 bits require about 7 gates of propagation. The output is a signed number so no need to process negative and positive values separately.

This circuit uses 52 gates to process 2 bitrits, it simply amounts to a 64×4 ROM, and it must be replicated 3,5× so it's not very compact, and the rest of the adders require even more gates.

Furthermore, the running disparity must also be injected somehow : that's the 8th value to add, since there are 7 bitrits and the adder tree would be unbalanced. So the running disparity accumulator from the last word is added with the 7th bitrit.

The circuit needs to be run (pipelined) 8 times, for each of the 8 possible counter values, while the serialiser outputs 8 bitrits (7 data, 1 counter), so the phases could overlap but the evaluation must be complete before serialising can start: it's a pipeline (eval, serialise) with 8 sub-cycles

....

Reducing the bias apparently requires a lot of effort. More than would be reasonable, probably.

Modern links rely on the scrambler to even things out, methods like 8b/10b are out of fashion for a decade now.

Better DSP front-ends can digitally handle the droops and wanders... I can't afford that though.

Adding a bitrit expands the words to 16 bauds, to transmit 16 bits : the ternary recoding allows the 50% expansion. And there is still one unused bit.

I'd like to avoid the above circuit but I know my AFE is lousy and would need some serious help, but is the expense/complexity/latency justified ? Is there a simpler method ?