I was reading  Colin O'Flynn's excellent "Forget Not the Humble Timing Attack" article in PoC | GTFO this morning, and I thought I should check how easy timing attacks would be in Java (I know, I know...). 

Anyway, turns out the System.nanoTime() is quite handy. Here's the sample demo that uses it to measure method invocation times for different key sizes:

import java.util.UUID;
import java.util.Arrays;

public class TimingPoC {

    private static char[] secret = UUID.randomUUID().toString().toCharArray();

    /** leaky password check **/
    public boolean checkSecret(char[] pwd) {
        for (int i=0; i<pwd.length; i++) {
            if (pwd[i] != secret[i]) {
                return false;
            }
        }
        return true;
    }

    public void start() {
        for (int i=1; i<secret.length; i++) {
            char[] candidate = Arrays.copyOfRange(secret, 0, i);
            long[] times = new long[5];
            for (int it=0; it<times.length; it++) {
                long start = System.nanoTime();
                checkSecret(candidate);
                times[it] = (System.nanoTime() - start);
            }
            Arrays.sort(times);
            System.out.println(i + "\t" + times[(int)Math.floor(times.length/2)]);
        }
    }

}

 And here are the corresponding (nanosecond) response times:

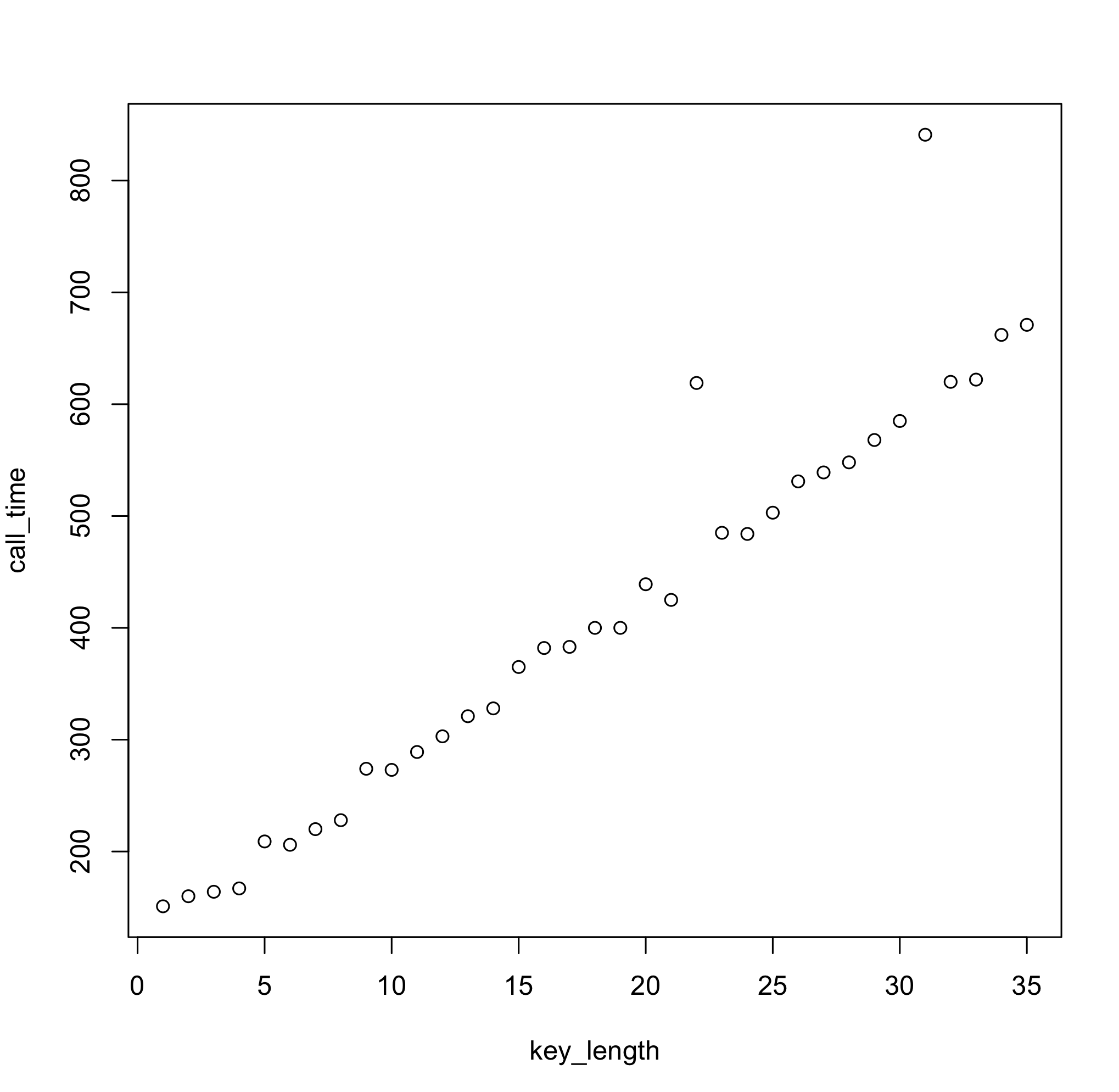
One simple linear regression later...

Call:
lm(formula = call_time ~ key_length)

Residuals:
    Min      1Q  Median      3Q     Max 
-37.185 -21.977 -10.429  -1.134 214.983 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 111.9210    16.7010   6.701 1.24e-07 ***
key_length   16.5838     0.8092  20.495  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 48.35 on 33 degrees of freedom
Multiple R-squared:  0.9272,    Adjusted R-squared:  0.925 
F-statistic:   420 on 1 and 33 DF,  p-value: < 2.2e-16

We can easily conclude that every extra character in the key length increases the method response time by 16.5 nanoseconds, which is the information that given naive password check information leaks. Now, all we need to do is keep increasing test key length until response times stop growing, and we'll have our target key size.

One thing to keep in mind with the approach above is that, on a modern OS, given times will not be deterministic. So repeated measurements are needed in order to get a "smoothed" value (in the code above value used is the median of 5 measurements). That said, though, in purely statistical terms, even more measurements would yield a more stable estimate, in this particular case, it's not necessarily true. Here's an example of a median based on 5000 samples:

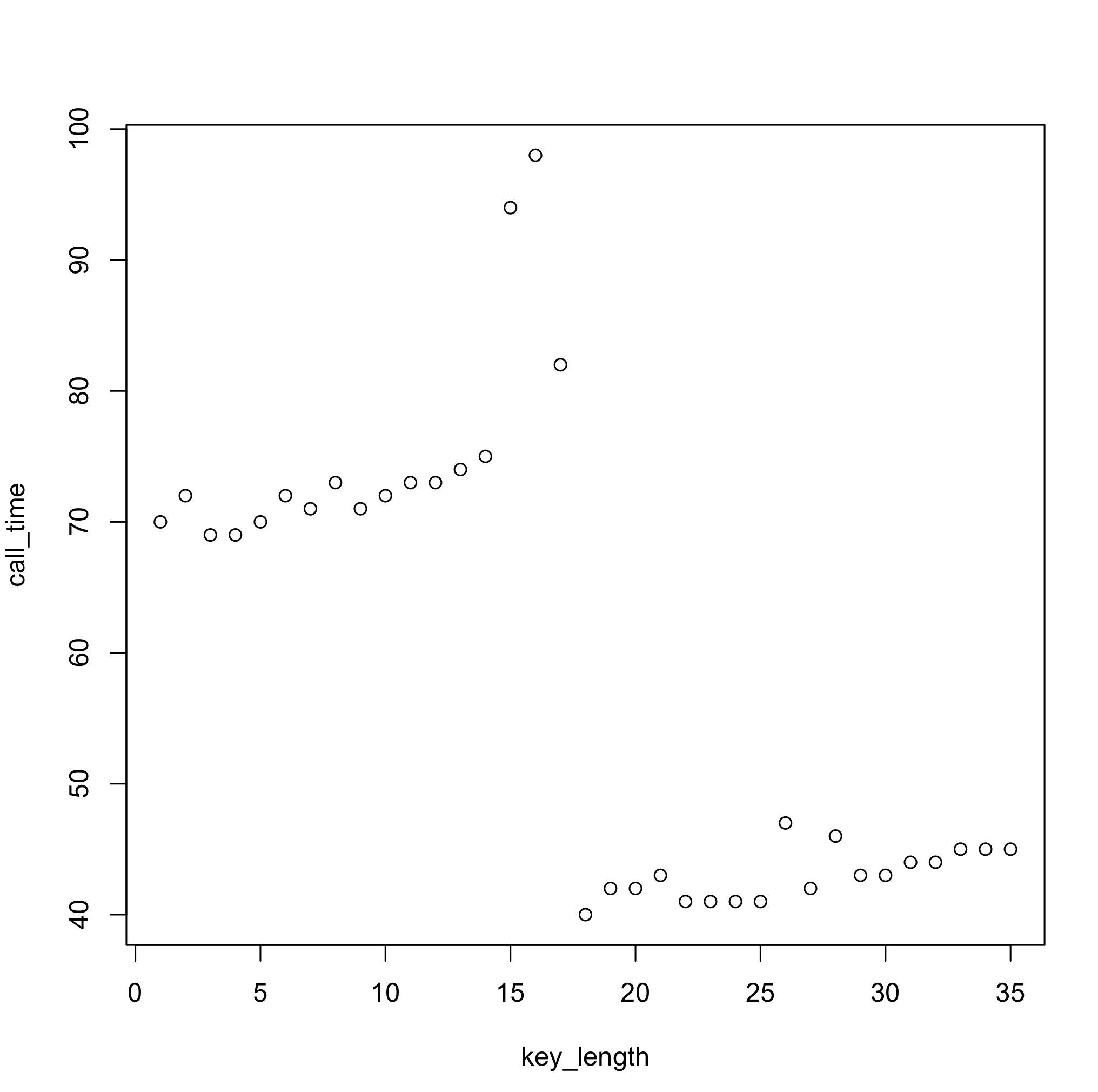
Why do you think this is the case? :)