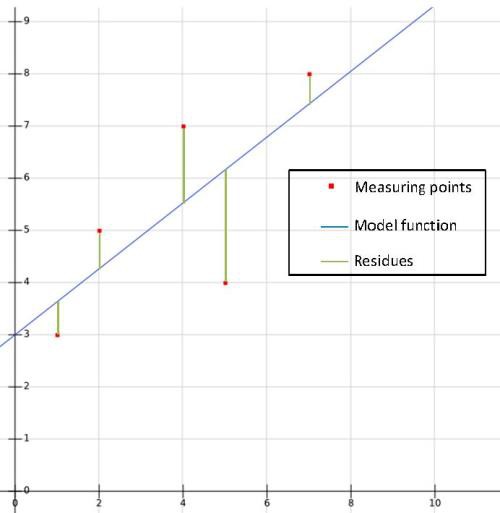
Linear regression can be used for supervised machine learning. The graph below shows measuring points (input and output values) and its distance (residues) to a function computed by the method of least squares (line).

The model function with two linear parameters is given by

For the n input and output value pairs (x_1,y_1),...,(x_n,y_n) we are searching for the parameter a0 and a_1 of the best fitting line. The according residues r between the wanted line and the input and output value pairs are computed by:

Squaring and summation of the residues yields:

The square of a trinomial can be written as:

Hence:

We consider the sum function now as a function of the two variables a_0 and a_1 (the values of the learned data set are just considered as constants) and compute the partial derivative and its zero:

Solving the system of linear equations:

Substituting

as the arithmetic mean of the y-values and

we get:

Replacing a_0 in the equation

yields

Because

For a new input value

the new output value is given by

or