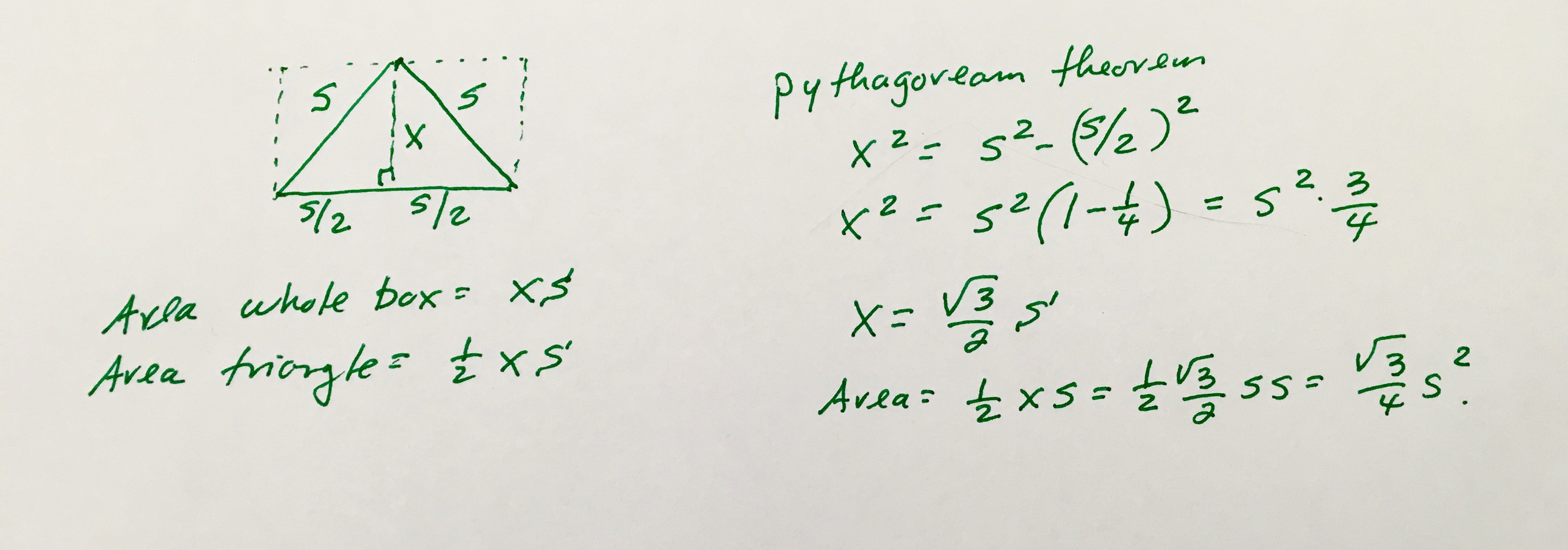3D Prints for Teachers of the Visually Impaired

It t has been a busy couple of weeks! We were excited to hear that this project has made it into the final round of the Hackaday Prize. It has been great to build this community of people who take the time to follow this project.

Another good thing that has happened is that we've been hearing about groups developing 3D printable models for the visually impaired elsewhere, and we are in the process of tracking these groups down and seeing if they would like to join forces in some way. (Any other suggestions for collaboration are welcome- feel free to send us notes in the comments or send a private message.)

We took an assortment of our models to a Hackaday meetup in Pasadena in a bar a few days ago, where it became something of a magic trick to remind everyone of their middle and high school geometry. (Rest assured that we just used water to prove that the models were all the same volume- no stronger beverages were harmed in testing this project!)

Our big issue now is that we have enthusiasm on the part of teachers of the visually impaired, but we still need people to take on creating the models. We suspect that the main issue is that it's not yet the "project time of year" in schools, and we may get upticks as CAD classes get to the point where students can take on a project. If you know civic groups, hackerspaces or teachers who might love this project, please pass it on!

We were thrilled to get our first "in the wild" collaborator, a group that volunteered to make Braille letter tiles that help kids learn Braille.

We also heard that the first teacher of the visually impaired (that we know about, anyway) printed and used the constant-volume cones. He sent us this picture of the student learning the same way we show us testing it in our video.

Speaking of our video, you can watch it here. Rich used YouTube's captioning tools so as many people as possible could understand what we are trying to do.

Now we will keep publicizing the project and encourage groups wanting a fun 3D design project to jump in and claim a model to do. We look forward to your comments!

We had the opportunity of presenting this project in a Lightning Talk at the Hackaday Pasadena meetup last night. In particular we asked people to help out with creating the designs that teachers of the visually impaired had asked for. Afterward a few folks who teach or are taking CAD classes at the college level came up and asked if they could participate. Of course! We had gotten so focused on K-12 teachers that we had not really reached out to that group. If you have CAD students needing a project, by all means claim one of the categories and go for it.

Over the last week we have also gotten questions about whether we had reached out to the Special Ed community in general to see if there might be interest from teachers who are helping students with other special needs. Let us know in the comments here or in the Google Group if you have any thoughts on this.

[Whosawhatsis] posted constant volume models on Youmagine, as reported in a previous log post. One of our teachers of the visually impaired gave us feedback that the points on that version were, well, too pointy for a blind kid to handle comfortably. We wrestled with options. Truncate the conical models a bit to make them a bit squared-off? We tried that but since the printer will drool a bit at the end we still got a pretty pointy point. Also, there's the issue that we did not want to distort the shape too much, since truncating cuts off some volume and might leave the wrong impression.

What [Whosawhatsis] did next was to add a different version of the models that have a little ball on top (see the image that follows) on the two models with pointy tops. We figure this will keep the original shape (since these are, after all, to learn about geometric shapes) without an uncomfortably prickly top. We are waiting to hear what the feedback is on this new one.

Our Google Group has attracted some members and we are noticing interesting things. First, teachers of the visually impaired who want to ask for models seem to want us to curate them a bit first and post for them. Maybe this is because we posted so many up front that it sort of looks moderated or like they have to do that, but we'll roll with it for now.

Second, we noticed that the most views are for the simplest object that we already made -- the volume-comparison examples, which have now been downloaded 303 times on Youmagine.

No one is calling dibs on making models though, so far - we thought we might get 3D printing after school clubs at the beginning of the year (and still might) but perhaps we will get more energy when project time rolls around in the spring.

Meanwhile, in case you're just a hacker who likes to make models to help people out - you don't have to be a teacher or student to fulfill a request, since there are always more requests where these came from. Go for it!

Comments, of course, always welcome.

When we created the Google Group (as written up in the last log) we promoted it via our social media and educational contacts.

A few days into posting our Google Group to get participants we noticed that we had accumulated a few members, but not yet any volunteers to try and create model files. We went back and reworded some parts of this project (based on some suggestions from teachers of the visually impaired) and encouraged a few friends in particular to get out there and either put out more requests or claim a project for their students to do.

We were concerned that perhaps teachers were reluctant to claim a model in case their students could not successfully complete the project. We changed the wording a little there too and have added a general "questions and say hello" thread to see what people are thinking. Let us know in the comments (or in the Group) if you have suggestions!

In the previous logs we talked about the basics of Braille and other issues specific to the visually-impaired, and then about creating sophisticated visualizations and extensible models. Then in the third and fourth log we looked at very helpful but very simple models, which are now up on Youmagine. In this log entry, we capture what we think the next steps should be to scale up this effort to allow more people to help.

We debated the various options: start a repository ourselves, create an area on an existing repository, or just create an online group for now where people could interact. Since we found when we participated in various volunteer activities to create models like this that a few iterations were usually required, for now we are just setting up a Google Group.

https://groups.google.com/forum/#!forum/3dp_edu_models

Check out the instructions on how to contribute (or to request a model if you are a teacher of the visually impaired yourself). For now the group is public but requires registration. We will see how the spam situation evolves, but hopefully it will be manageable.

We have made it minimalist and deliberately NOT visually-oriented, so that visually impaired people using screen readers can (we hope) use the group as well. If anyone tries it please let us know in the comments any issues that arise.

We have seeded the group with requests from our friend Lore Schindler from LA Unified School district. If you have students who need something to do with that new 3D printer, jump in, pick something to work on, and go for it!

When we showed the models in the last build to Lore Schindler (our test teacher of the visually impaired) she liked that the models were hollow and that the students could fill them with water to discover that the volumes of the objects in the set were the same. However, she also wanted to have the students be able to close the models and have them feel the object with its missing side present- in other words, in the case of the cylinder, to have a soup can and not a cup.

She asked for a hinged bottom, but that would have made it harder for the models to be easy to print, without support. So instead we added a lid for each model. This required changing from a vase print to a wall with finite and predictable thickness. In the process, we modified the code to make the interior volume match instead of the exterior volume. This way, you can prove that the volumes match by pouring liquid from one to the other.

The picture shows four geometric shapes that are all the same volume. A cone has one-third the volume of a cylinder of the same base area and height, so the cylinder is one-third as high as a cone with the same base area.

You can prove this to yourself by filling one with water and pouring the water into the other one.

We know from Cavalieri’s Principle that a cone and a pyramid that have the same height and same base area as each other have the same volume. We have also included two pyramids that have the same volume as each other, and which have the same base area as the cone and cylinder.

How did we calculate the area of the pyramid base? The little drawing here reviews the math to analyze the area of the base. Imagine the triangle shown here, which has three sides all of length s and is of an unknown height x. (Note: we will use a caret - “^”- to show raising to a power. Thus x^2 is x squared, and so on. We will use a star for multiplication and sqrt(x) for square root of x, and the usual slash for division.

If we use the Pythagorean theorem, we get that x = s*sqrt(3)/2. The area then is s^2*sqrt(3)/4.

That’s not too hard, but we wanted to make it the same as the circular base of the cone and cylinder. We wanted to have formula that worked for both.

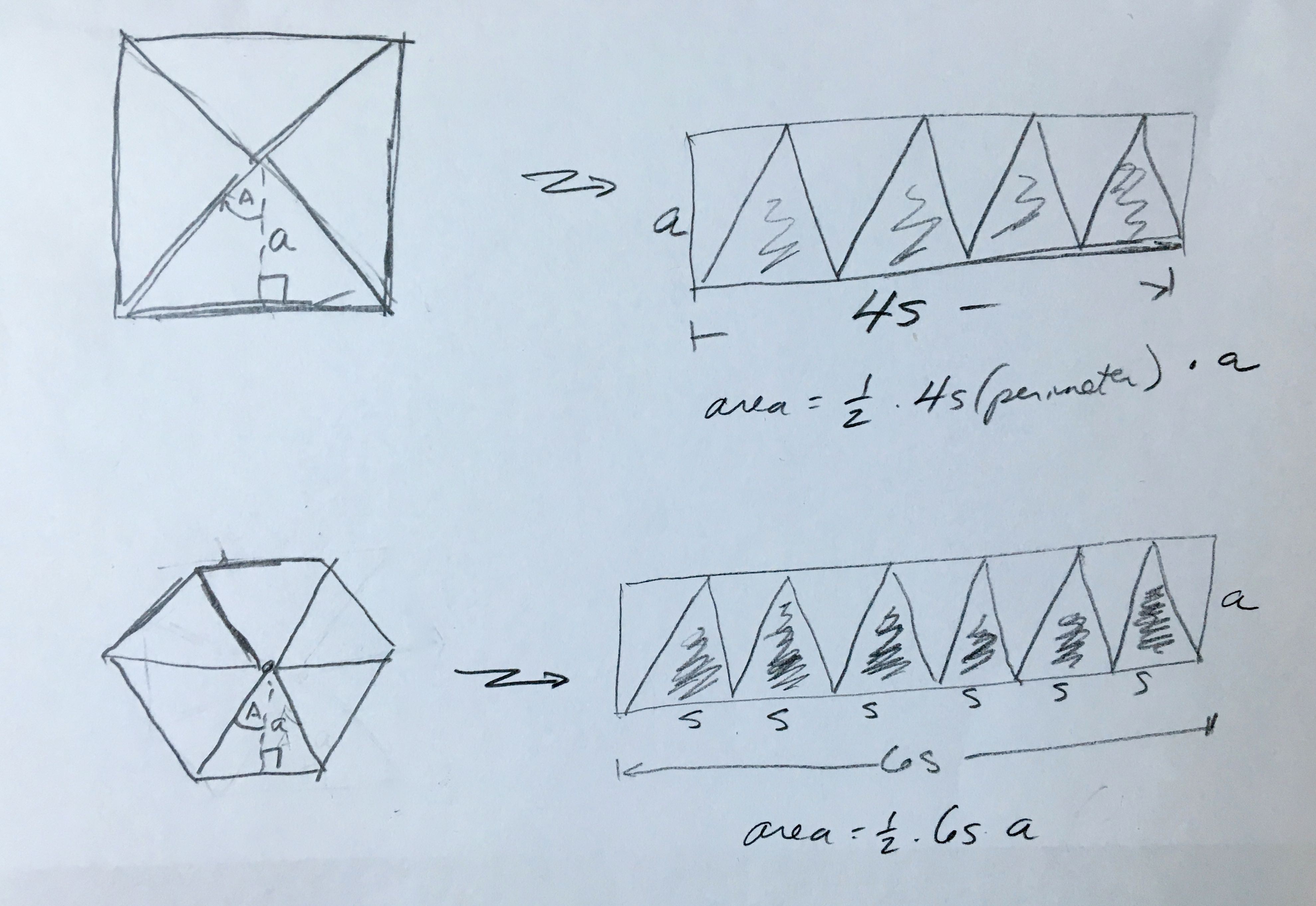
To do that, we used the apothem. The apothem is the distance from the center of any regular polygon to a side, measured perpendicular to that side above. In the case of a triangle it will be the length of a line connecting that side to the center (a, in the diagram that follows).

So instead of considering our triangular base as just ONE triangle, now it makes more sense to think of it as three triangles (because any regular n-sided polygon can be thought of as being made up of n identical isosceles triangles). A square becomes four triangles, a hexagon six. The area of each of these is the apothem times half its base. You can get the apothem length by determining the angle A at the center of the polygon, which is 180 degrees/n. The apothem will be the s/2 * tangent(A) (or, if you prefer, s * tangent(A)/2.)

For regular polygons with n sides, the area is n * s * s / (4 * tan(180/n)), which also happens to be half the perimeter times the apothem. To see this, note that the area equals perimeter * apothem / 2, since the apothem is s / (2 * tan(180/n)) and the perimeter is n * s.

As the number of sides increases, a regular polygon gets rounder and approaches a circle. As this happens, the apothem and radius (the distance from the center to any corner, in the case of a polygon) converge toward the same value, and the perimeter asymptotically approaches 2 * pi * r. This means that the area is (1/2) * (2 * pi * r) * r, which simplifies to pi * r^2. In the case of our OpenSCAD model, the “circle” is a polygon with hundreds of sides approximating a circle, just to make this point. [Whosawhatsis] likes to think about this as “unrolling” the triangles into a rectangle as shown here. The area of the whole rectangle is the perimeter times the apothem, so the area of the triangles making up the polygon is half that.

We will post the link to the OpenSCAD that created these as part of our next update.

Our sophisticated 3D printable math and science models discussed in the last log were aimed at teachers and students who wanted to be able to use them as the basis of a solid science fair project, or perhaps to use as a visualization in class. However, when we started polling some teachers of the visually impaired for what they wanted, some of the requests were surprisingly simple.

For example, one suggested model was a set of basic shapes (cylinder, cube, etc) all with identical volumes, and open on one side (for the first version, we simply printed in "vase mode". Teachers can use these with some water to show that the volumes are all equal. Visually-impaired kids can then also explore these hollow models with their fingers.

A little bit of remembering your high-school geometry will also bring back that the volume of a cylinder is three times that of a right circular cone of the same height. It turns out that this holds true for pyramids (which are just cones with a polygonal bases instead of circular ones). So our next set was to prove these relationships.

However, a hollow cone without a bottom is a little tricky to print. These were also solid objects printed without infill, but we left the bottom open instead of the top. Because our normal printing settings included printing the lines of the first layer with 200% width, this created a small inverted brim on the inside, which made them easier to print and could be peeled away after printing. They could be printed without support.

After we had thought about labeling models, we got down to the basics: what does it mean to create a 3D model of something? For a physical object, it's obvious- it's either a scaled-down model of something big (like a house), or a model of something that's not normally accessible (like the bones in a hand). If it's something that is sort of fist-sized and accessible, then the blind person might as well just feel the real thing.

Books for the blind often have raised-line drawings, labeled in Braille. We wondered: how well do blind people process 2D projections of 3D objects? Think of the common illustration of a cube as two squares with their corners connected. If you raise those lines so that you can feel them with your fingers, are they going to feel even remotely like an actual cube? A photograph or a diagram like this looks like its three dimensional counterpart to sighted people because we're used to viewing the world as a projection from three dimensions down to two. Even stereoscopic vision isn't truly 3D, and the lack of depth perception in a still photo or a movie doesn't interfere in the least with our ability to recognize shapes.

A person who has been blind from birth, on the other hand, has never seen a cube as three parallelograms (the three visible faces, with the other three occluded). Even if you have a cube made of wires following the edges, with nothing in the center, you might be able to turn it so that it is visibly identical to a wireframe cube drawing when viewed from some specific angle, but the shape of the raised lines will feel nothing like that of the wires making up the real cube. We've been told that it's usually very difficult for a blind child to learn to understand concepts like "behind" and "in front of" because unlike a sighted child they're not constantly unable to see certain objects because they're occluded by other objects in their 2D field of view.

3D graphs in text books can be particularly tricky to translate into 3D (even for a sighted person). Would it be better to provide (if possible) a 3D version, rather than raised-line drawings of 3D projections?

As we were thinking about this, we were fortunate to get a contract for our Apress book, "3D Printed Science Projects," which came out in May of 2016. (The flower, gear and wave in the gallery are from the book; the book is available from Apress at the given link. The models (but not the book itself) are available at the same link under a Creative Commons, Attribution, NonCommercial Share-Alike International 4.0 License.)

For the book, we came up with a lot of models that were both easy to print and able to be varied to some degree on the science involved. We discovered there were several types of models:

• Entirely abstract ones that are just three-dimensional graphs, that perhaps show one quantity in two dimensions (often two dimensions of physical space) and a related quantity in the third. Example: a model of orbits that shows the orbit plane in two dimensions, but the height of the model around the orbit is how fast the body is going at that point in its orbit. The picture that follows is the orbit of Halley's Comet plus the set of orbits of Earth, Venus and Mercury. The Halley's orbit is not to the same scale as the other three. (From 3D Printed Science Projects.)

• Models that are sort of representing a physical object, but perhaps a physical characteristic is simplified or modified a little to make a point. The flower model in the Gallery would be in this category.
• Visualizations of physical things that are too small (molecules) or too big (like terrain or some architectural features) to be seen or felt by humans. If the point is to show how these things fit together too it can get tricky.

Things we learned:

1. Almost every textbook illustration of a given phenomenon is the same as the others out there, and that very often the 2D projection used for years by every book is, at best, misleading.
2. Creating a good model is difficult and requires deep knowledge of what you are modeling.
3. Deciding on what detail to put in and what to leave out is a delicate balance.
4. Iterating models like this takes time, and they don't stand alone- the book's explanations of the science is a really necessary package with the model itself, except for a few self-evident ones like some simple machine models. Documenting assumptions and simplifications is just as important as what it does include, particularly if the intent is that a student will add on to and alter a "starter model."

What this means for this project is: models take time; they require some real thought about what to show and how to show it; and the creator gets a lot of insight into the science or math when developing the concept. This says that creating a model will indeed teach a student a lot about the subject, but that there was going to need to be some capturing of documentation and vetting of accuracy for the models to be broadly useful- in other words, some sort of contest or wiki-like review.