Main revision:
I have implemented a new algorithm for mapping the mesh. Instead of each node doing BFS, I’ve decided to have one node do BFS, then send its map to the others. I coded up a method that will locally calculate the best paths through the network based on the tree structure given.
Results:
- On a network of 100 nodes (<=6 edges per node) the new algorithm is usually near 98% more efficient based on count of packets transmitted.For similar networks of 100 nodes with <=6 edges per node, the old algorithm transmitted around 3.5 million packets. The new algorithm transmits around 72,000 packets. This packet count does not account for packet fragmentation which would certainly need to take place, but that is handled at a different layer. Actual packet count would be higher when fragmentation is accounted for in the real world.
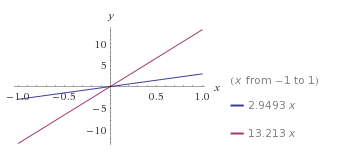
- Notably, the old algorithm’s linear trend line was y=13.213x whereas the new one is showing numbers around y=2.9493x meaning that this new algorithm is actually reasonable for large networks.
- Update: On a network of 254 nodes with <= 6 edges per node, the new algorithm uses around 490k packets compared to 70 million packets on the old algorithm. That's just 0.7% of the previous traffic.
Worst case performance:
- Assuming that an undirected graph can have
edges, and that my maximum supported network size is 254 nodes (for implementation reasons) I should have a maximum complexity network consisting of 254 nodes and 32,131 edges. My implementation of storing and sending the network map requires this many bytes (where n = node count and e = edge count)
If we substitute in the max edges we have a maximum byte count of:
This works out to 64770 bytes. Assuming a maximum packet payload of 32 bytes, that’s 2025 packets. After adding in the other packet header info (14 to 17b) for 2025 packets, the actual byte count is 34,425 + 64770 = 99195b. On a best-case scenario of 200kbps throughput, this might allow the full map to be transmitted from one node to another in 0.49597s, and (since in this case each node can see every other node because we are doing max edges) it would be propagated to the rest of the nodes in 2.09min (excluding the tree processing time taken between propagation steps).
- Two minutes sounds slow, but to think that the network is fully decentralized and has 250+ layers of redundancy is remarkable. Note that this figure is propagation time, not including initial mapping time (this would also be a significant amount of time due to network complexity.
- For clarity's sake, the above "worst case" is basically when you stick 254 nodes in a single room where they're all in range of each other and then you turn them all on. Hopefully you're not going to actually turn on more than 5 or 6 nodes in a single room (why waste more?) which would be virtually instantaneous to map.
Challenges:
- The simulator is currently experiencing a stack overflow problem for very large networks on the new algorithm only when debug messages are turned on. If debugging is set false (it is by default) then no problems occur. I’m planning to talk with some CS friends to see if we can make that go away.
- This implementation will be a little trickier to implement in hardware, so I’ll need to familiarize myself a bit more with the existing libraries for smooth integration.
I'll continue doing some work on getting this into hardware as I can. I'm trying to get much of this code into the RF24Network library because that's a pretty robust starting point.
Source Code:
The source code for the new algorithm simulator is available on GitHub under master/AlgorithmTwo. Enjoy!
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.