One feature of the algorithm that's been missing so far is a proper rotational symmetry. I've already implemented a point symmetry to get the same result as a 2-fold rotation; it's fast and the code is simple but not generalizable to n-fold rotations. What I find especially cool is 3-fold symmetry. Here I'll explain how I coded the general symmetry and present some results.

According to the original algorithm, the rotational symmetry is applied to the activator and inhibitor arrays of each scale, before looking for the best variations. Each pixel/array element is averaged with its symmetrical points around the origin of the image. The number of averaged pixels depends on the symmetry order. First we'll see how the symmetry works in practice, then to which part of the image it should be applied, and finally an idea to organize all this data.

---

Rotational symmetry

For the moment, let's forget the Turing patterns, forget that we will work with data arrays and just focus on the point symmetry in a 2D coordinate system. We have a picture, assumed square, with a width 2r, and the origin at coordinates (0, 0).

Let's also assume that we want the picture to be point-symmetrical around the origin, with an order of 4. That means that the image will be four times the same sub-image, rotated around the origin.

There's a point at coordinates (x0, y0) which symmetrical points we want to find. If we draw a circle centered on the origin and passing by (x0, y0), the first symmetrical point is also on this circle but rotated by one fourth of a full circle, that is 2π/4. This gives the coordinates (x1, y1). The second symmetrical point (x2, y2) is found by the same method and a rotation of 2*2π/4. And the last point (x3, y3), same thing with a rotation of 3*2π/4. In the end, we have four points that are symmetrical around the origin.

In general, for a symmetry order s, the rotations of the (x0, y0) point around the origin will be the angles

where

Obviously, s = 1 is a special case with no symmetry at all.

Concretely, how to compute the coordinates of the points symmetrical to (x0, y0)? Knowing the angles θ, the rotation is done with

Looping through the values of i, it's easy to make a list of all symmetrical points to (x0, y0). And if these two formulas are applied to all points in the appropriate portion of the image (for a symmetry order s = 4, that's the top-right quarter), we can list all the symmetries in the image.

---

Application

For the project, we have to apply these rotations to a 2D array (activator or inhibitor) and average the values of the symmetrical points. For example, let's work on the activator array act[x][y], again with s = 4:

1. Find the coordinates (x0, y0), (x1, y1), (x2, y2), (x3, y3) thanks to the formulas above.
2. Compute the average avg = (act[x0][y0] + act[x1][y1] + act[x2][y2] + act[x3][y3]) / 4.
3. Replace the values in the array, i.e. act[x0][y0] = avg, act[x1][y1] = avg, act[x2][y2] = avg and act[x3][y3] = avg.
4. Loop steps 1 to 3 over all act[x][y] with (x, y) belonging to the top-right quarter.

Here, step 1 is done on-the-fly. This requires computing rotations each time we want to symmetrize an array. But if the symmetry order is fixed, it's more elegant to make a list of symmetrical coordinates at the beginning and just go through the list when repeating steps 2 and 3. Besides, it avoids computing cos and sin all the time, which could be computationally expensive (thanks to Jason Rampe for the idea).

First caveats about the rotation applied to a data array: the (x, y) values are integers, but we compute them with cos and sin functions which give floating-point values. So there are lossy conversions happening, and the rotation/symmetries are flawed. This isn't too worrisome if the resolution is large enough, because the couple of pixels badly symmetrized will be lost in the sea of correct ones. But it's still important to remember that the integer operations are not perfect. In addition, we're applying a rotation to pixels of a square image, so some of the rotated coordinates will be out of the image. For instance, a pixel in the top-right corner rotated by 2π/8 might end up out of bounds (see below).

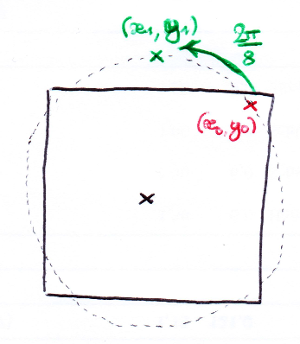
Second remark: since the image is represented by a data array, the origin isn't at coordinates (0, 0) but (r, r). The coordinates have to be translated for the computations to be correct, but it's very simple so I won't explain it in detail.

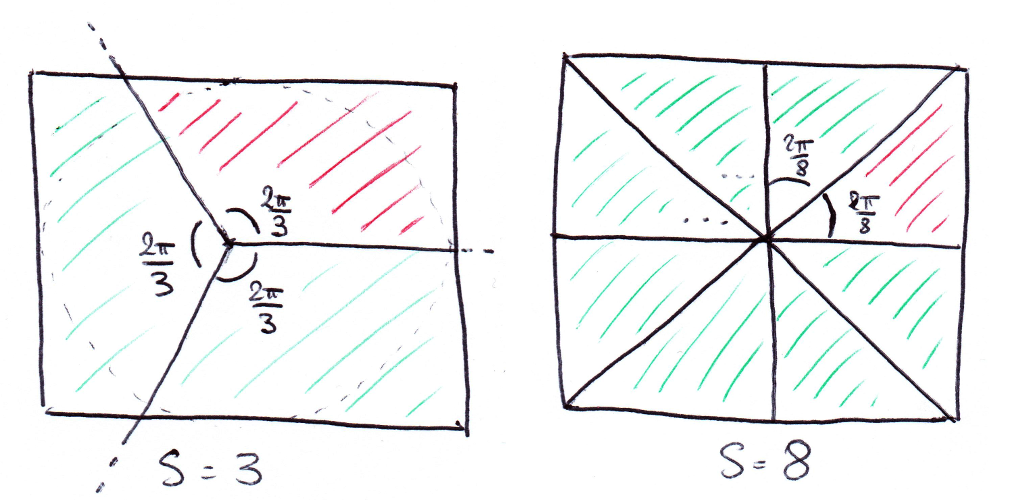
Third remark: like I said before, we only need to compute the symmetrical points of one part of the image, let's call it the "main zone". For s = 4, it's enough to make lists of four points: the first one being in the top-right quarter, and the three other ones being symmetrical to the first. For s = 2, just make lists of two points: one in the top half, the other in the bottom half. In the picture below, the main zone is red and the symmetrical zones are green.

The question is: How do we find which coordinates need to be part of the calculations? For s = 2 and s = 4, it's pretty simple because the main zone of the picture is square. But what about s = 3, s = 8? It's not so straightforward. Let's talk about that.

---

Defining the main zone

The main zone is one s'th of the total image area, and it is always part of the top half of the image (arbitrarily). For example, with s = 3 and s = 8:

Let's get back to a square image of width 2r and origin (0, 0). We have to find a general description of the coordinates included in the main zone. The first two conditions are simple: a point at coordinates (x, y) is in the main zone if x ∈ [-r, r] and y ∈ [0, r]. That just describes the top half of the image.

The third condition is on the relation between x and y. Depending on the symmetry order s (you can think about s as "in how many parts the image must be divided"), the main zone is limited by a straight line. We should distinguish three cases, as shown below:
- If s < 4, a point is in the main zone if its y coordinate is above the limit line.
- If s > 4, y must be under the limit line.
- If s = 4, it's a special case where the limit line is the y axis.

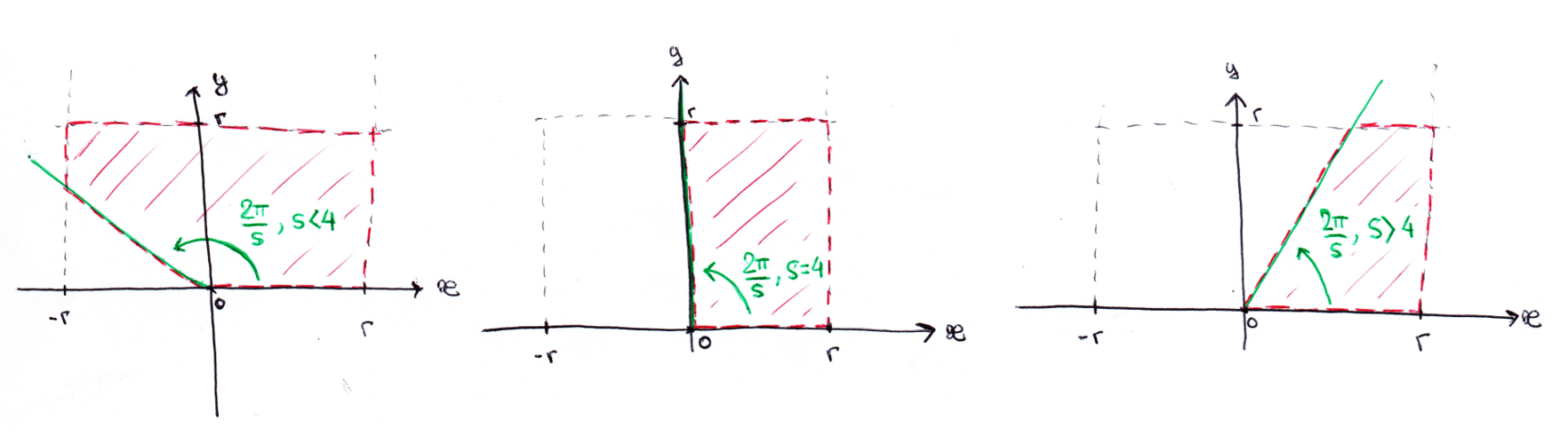
Since the limit line is straight, its equation is simple to find. It's So the third condition on (x, y) for the point to be in the main zone is:

In practice, the case s = 4 doesn't have to be coded as a special case, it can be integrated in one of the two others.

---

Data organization

So far we know how to check if a point's coordinates are in the main zone, and how to find the coordinates of its symmetrical points in the rest of the image. The number of points in the main zone and the number of symmetries for each point both depend on the symmetry order s and the picture size. In addition, because the image is square, not all rotated coordinates are within the picture. (For the moment I decided to not include them in the symmetry calculations at all, but another possibility is to wrap them around.) This means that in general, the program doesn't know the amount of data to store before runtime. So the data must be stored dynamically, and since we're dealing with lists, I chose linked lists as a data structure.

The general structure is a linked list of linked lists. For each point in the main zone, there is one "symmetry" object (actually structure, because it's C, but let's call it an object). This object contains two items of data: a pointer to the next "symmetry" object in the list, and a pointer to a "coordinates" object. A "coordinates" object contains three items of data: a pointer to the next "coordinates" object in the list, an x coordinate and an y coordinate. The list of "coordinates" objects represents all points that are symmetrical to each other and within the image's bounds.

---

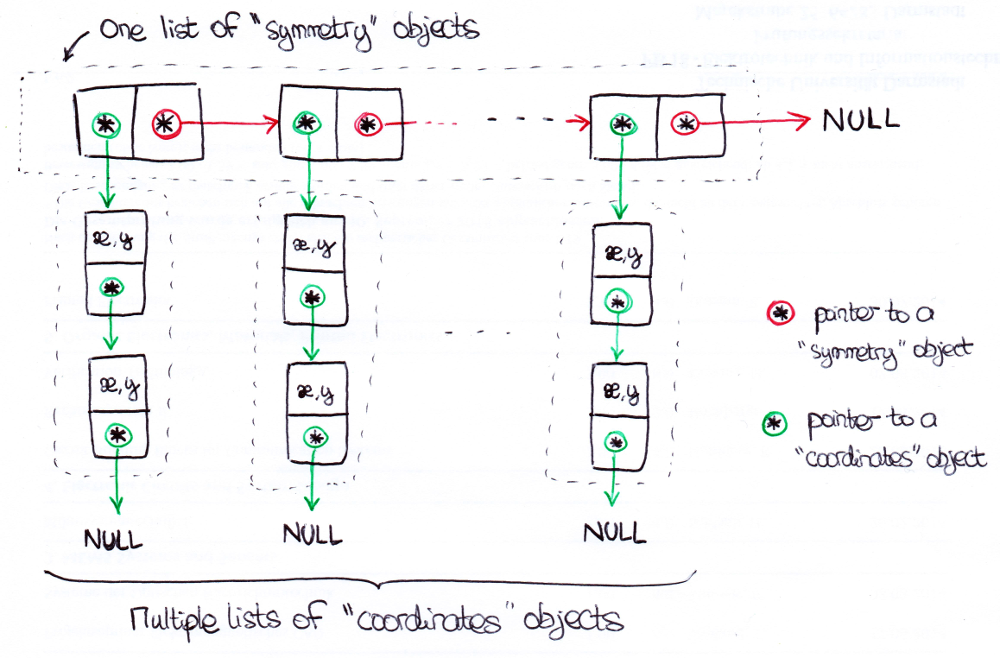
Summary

At the beginning of the program, before generating anything:

1. Create an empty "symmetry" list.
2. Pick a couple of coordinates in the image. If it's within the main zone (as defined by the three conditions in "Defining the main zone"), add a "symmetry" object to the list.
3. Create an empty "coordinates" list and make the lastly created "symmetry" object point to it.
4. Compute all the symmetries to the couple of coordinates by the rotation method. For each symmetry that is within the image, add a corresponding "coordinates" object to the list.
5. Loop steps 2 to 4 through all coordinates of the image.

And during the image generation, when applying the symmetry to the activator or inhibitor arrays:

1. Take the first "symmetry" object of the list.
2. Traverse the list of coordinates to which it points.
3. Average the values of all symmetrical points and replace these values by the average.
4. Go to the next "symmetry" object.
5. Loop steps 2 to 4 until the end of the "symmetry" list.

The results are PRETTY AWESOME if you ask me:

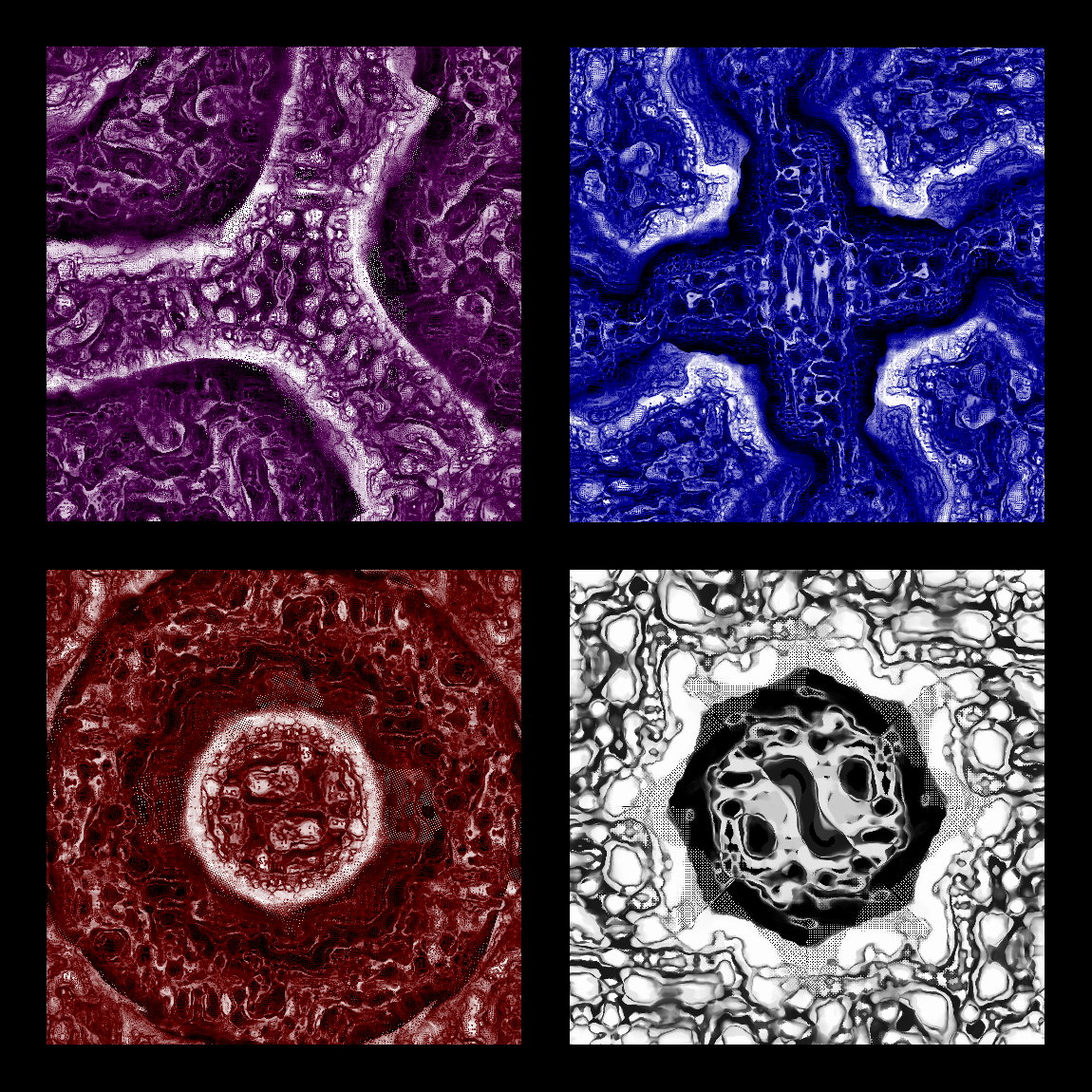There are some artifacts here and there, though. You can see that especially well on the bottom-right picture. I'll have to find out where that comes from.