After taking a detour (and dragging a couple of others with me) through the realms of ePnP, I’ve done an about turn and gone back to my original idea of using circles and their apparent ellipses for tracking position and attitude. I’ve already implemented most of the steps and I’m reasonably confident that this approach will work, though I still need to see how well it will sit on a 300MHz Cortex M7. Anyway, here’s the approach as it stands at the moment:

Take three sensor points in 3D space which have been lit with laser light (i.e. base angles are known). Construct a circle in 3D space using those three points and determine: the centre of the circle, the radius of the circle, the relative angles of the sensors around the circle and, the normal to the plane the circle sits on (use a combination of the three sensor normals to determine the outward facing side).

At the end of the process you should have something like this which shows a circle constructed from A, B and C:

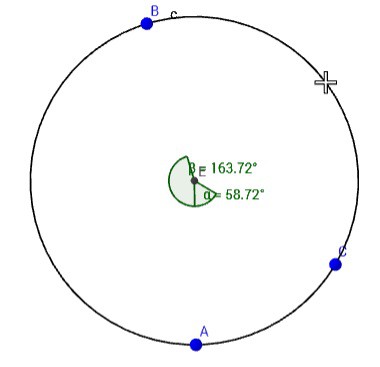
Once the 3D circle information is known then start working on the information from the laser sweeps. Use the relative angle/bearings between the sensors to determine the angular magnitude between the sensors (AB, AC and BC). These distances relate to a series of chord lengths around an ellipse with the defined theta angles between them:

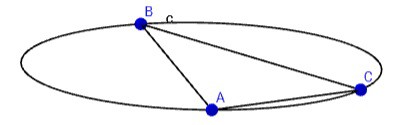
The following equation can be used to determine the length of a chord on an ellipse:

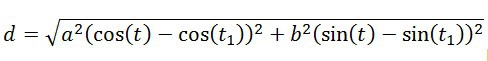
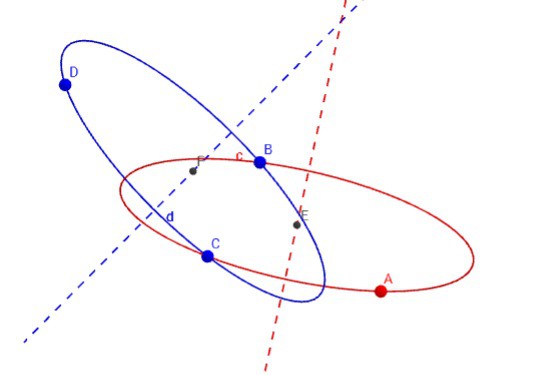
The problem easier due to the fact that, at this stage, there is only the need to match the ratio of the chord lengths with the ratio of the major/minor axis at those angles. This allows the removal of the minor axis as an unknown as well as the root. However, the problem is made more difficult in that the sensor group may be at any theta angle on the ellipse depending on the attitude of the HMD with respect to the base. This has the effect of “sliding” the sensor points around the ellipse as shown below:

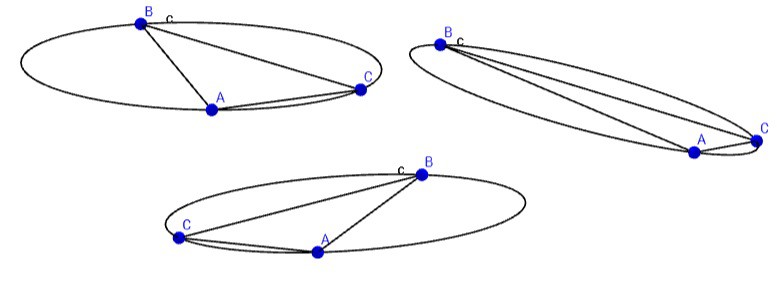
This basically boils down to a system of three equations where only R (axis ratio) and S (slide angle) are unknown:

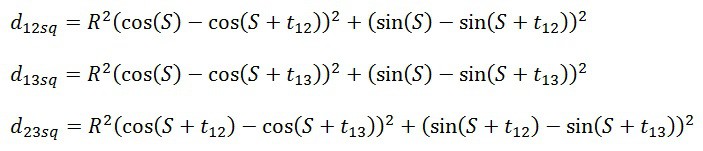
Unfortunately my mathematical skills failed me at this point and I have had to solve this part through iteration. I’m still hopeful that a colleague will take a look at it and come through with a less computationally intensive solution.

Perspective errors in the ellipse can be reduced by taking advantage of the fact that there are actually two “slide” angles in the ellipse which will fit the chords - exactly PI radians apart. Solve for the slide angle in 0<S<PI and also in the PI<S<2PI ranges then average the two sets of results (still to do in the code).

Once solved, this gives a major/minor axis ratio, chord lengths (with the minor axis set to one) and, the “slide” angle at which the chain of chords starts, and we start relating the two sets of figures, circle and ellipse together to figure out the pose:

• The ratio of the major/minor axis gives the angle the circle has been tilted from perpendicular to the base.
• The “slide” angle will determine how much the HMD has been rotated around the centre of the circle (in the plane of the circle), use an accelerometer to determine up and the correct angle
• The ratio of the original chord length vs the calculated one gives actual length of the minor axis
• Scale the minor axis up by the major/minor axis ratio to get the major axis length
• Use the major/minor axis to determine the positions of the points wrt to a zero and then work back to determine the centre of the measured ellipse from the scan.
• The centre of the ellipse is a bearing to the centre of the circle.
• The major axis is the angle created by the circle radius length – use both to determine the distance between the base origin and the centre point of the circle.

This is about as far as I have come so far. Through with use of external sensors and the sensor normals it should be possible determine the position and orientation of a base wrt to the HMD. Depending on how much this approach loads the processor I would also like to run this a few times on a few different sensors to reduce errors in the extremes of major/minor axis ratios (<1.5 and >4) where there are more uniform chord length ratios present. It would also allow the attitude to be better fixed by also locking vectors of other circles: