Solver

From open source to proprietary, there are tons of traveling salesman problem (TSP) solver available.

In operation research, TSP is one of mixed linear integer programming (MILP) problem. Compared to linear programming (LP),  the search space of MILP is discrete. Thus, it is NPC problem in complexity theory. In English, for such problem we haven't found an efficient algorithm that can solve the problem in polynomial time. 

To grasp the intuition what NPC is, let me give you an example. Let say we have N=64 switches, whose state can be either on or off. We have different real number outcome given the on/off combination of all 64 switches. Your goal is to try to find a combination such that it delivers a whatever optimal function you prefer.  There are 2^64 combinations! That's 20 of zeros in 2^64. If you use brute force search on its solution space, chances are you may not get your answer until the end of universe. Let say you can tests at the speed of 1000 combination per seconds, you need approximate 10, 000 billion years.

MILP problem is similar to the example I gave above. Although the problem seems to be impossible to solve within reasonable time in theory, it is not exactly the case in practice. Depending on the nature of the problem, we may be able to find an intelligent method to cut the search space so that reduce the number of candidate in dramatical manner.

In the last 30 years, MILP is a hot research topic. With algorithm improvement and beefy computer hardware, we can solve a lot of MILP problem by computer. The Traveling Salesman Problem book [1] gave a good survey on this topic. I borrowed it from NCSU library and read it as I wrote this log. The book is well written and easy to understand even for operation research outsider like me.

Data

We kind of know the approach to solve the problem. But we need data. 

Most of the time at work, acquiring data is always more challenge than solving the problem itself. I'm not kidding. Data is asset to any company but not the algorithm. Google can publish or even open source its page rank algorithm without losing its technological advantage to others. Because very few company has such large volume of user data.

In part order optimization, the related data is right in the Cura slicing pipe line. To extract them, requiring some time and effort to understand Cura source code. I spent two weekend in doing this. To save your time, I wrote a developer guide and shared my source code notes. 

In my modification, I output three text files: 

1. parts data file.

2. entry point and exit point of part data file.

3. parts optimized order data file.

For more details, please check out my wiki.

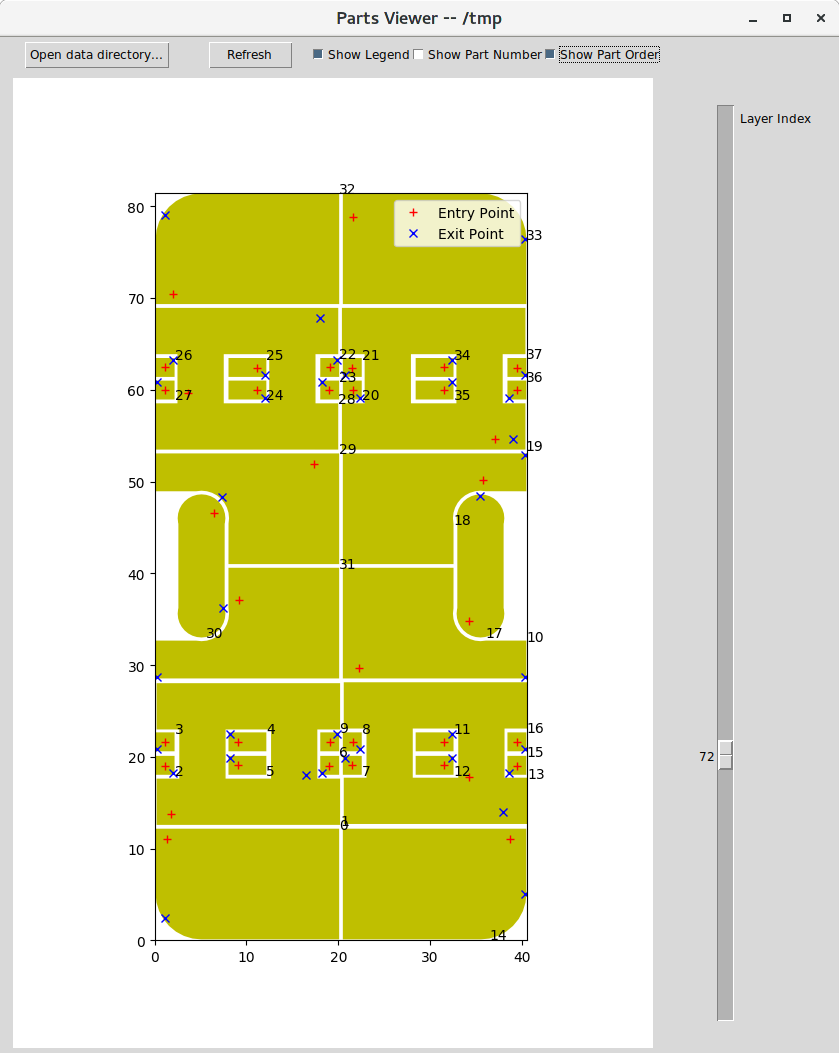
I also wrote a matplotlib TKinter UI to visualize all three data files. The drawing algorithm is quite interesting. Because for any part, there might contain more than one closed polygons. The first closed polygon is its outer perimeter. Any closed polygons other than the first one are the empty space of parts. Although a part is defined as a closed polygon has no overlap with any other part, it is possible that other part reside in the empty space of parts. To make the drawing right, we need to perform topological sort on part. Any part that reside in the empty space of other parts needs to draw after other parts being drew. Otherwise, drawing empty space (i.e. filling in a white color) will cover those parts. 

In any case, here is what you got in the end. I did a few sampling test. The entry point and the exit point matched the tool path simulation in the latest Cura. From here, I will study the TSP academic book and work on implementation.

Reference

1. The Traveling Salesman Problem - A Computation Study. David Applegate and etc. Princeton University Press. 2006