In bootcamp #1 you learned how to use some simulation tools and build combinatorial logic -- that is, logic that doesn't depend on the previous state of the system. That's fine for some things, but a lot of practical systems need to remember their previous state or even states.
To do that, you'll usually use a design that incorporates flip flops. A logic gate that has two states and can be in one state or the other. You might think, "Well, an AND gate has two states: 1 and 0." That's true, but that state depends completely on the inputs so it is a combinatorial gate. A flip flop will maintain its state even when its inputs change -- unless they change in the specific way that tells the flip flop to change state. This is the basis of many kinds of computer memory, for example.
There are several reasons this is exciting. Obviously, if we need to remember a state (the traffic light is currently red) this is the answer. But the way flip flops work also solves an important timing issue that we talked about in Bootcamp #1 -- how to make sure different processing times (propagation delays) don't cause glitches in outputs.
We'll talk more about that during this bootcamp, but here's the quick explanation:
Remember this diagram from Bootcamp #1?
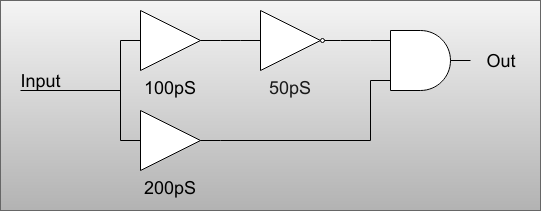
In this case, the AND gate will possibly get "bad" inputs for about 50pS when the top input register a change before the bottom one comes in. Now assume that there are lots of other inputs to the AND gate with different times. Keeping track of this could be a real problem and even if you know the longest path is, say, 500pS, that doesn't help you stop the glitches. For the sake of this example, suppose the longest is 500pS and the AND gate itself adds another 400pS.
That means the longest path from Input to Out is 900pS. When the input changes, the output could be wrong--and even change incorrectly--during that 900pS window. But what if we put a flip flop between the AND gate and Out?
Each flip flop has a clock and the outputs can only change on a clock edge -- usually the positive edge. As long as the clock is not at an edge, the output of the flip flop won't change. So if you arrange for the clock edge to be at, say 1,000pS (1nS or 1 GHz) or longer, then it won't matter if the AND gate glitches or not. The glitches won't get past the flip flop (sometimes just called a flop by designers) and then once stable the flip flop will change states.
That sounds great, but of course there are pesky details. For example, that assumes the input is changing in sync with the clock. If it isn't you are opening up to metastability -- something we'll talk about in a future bootcamp. The reason is the signal into the flip flop has to be stable a little bit before the clock edge (set up time) and a little bit after the clock edge (hold time) or you'll have problems.
Another problem is what happens when your delays are not very tiny but are, instead, very large. If the delay is 1mS, your clock would have to be less than 1 kHz! There are several possible answers to that problem, including pipelining, which we'll talk about in the future.
For now, though, we are going to focus on developing simple systems with flip flops and leave the complex details until after we've figured that out. The demo design will keep the adder from last time but also include a latch that remembers if the adder ever generated a carry and a few counters to get the onboard 12 MHz clock down to a 2 Hz rate to drive blinking LEDs.
This bootcamp is part of a series:
| Bootcamp 0 | Covers basic digital logic concepts with simulations |
| Bootcamp 1 | Introduction to FPGA coding and simulation with combinatorial logic |
| Bootcamp 2 | More FPGA coding and simulation with flip flops (sequential logic) (this bootcamp) |
| Bootcamp 3 | Working with actual FPGA hardware |
When you are ready, move on to the steps and continue on your FPGA adventure! You'll also find background articles in the project logs. You might want to browse them first and refer back to them as you work through the steps. The logs also have a glossary you can check for any unfamiliar terms.
 Al Williams
Al Williams