I made a big mess on the bench, and got some decent data using the toy sampling head and the delay generator. Despite the look of a terrible layout, it manages 100 GS/s (equivalent time) and 180 MHz front-end bandwidth.

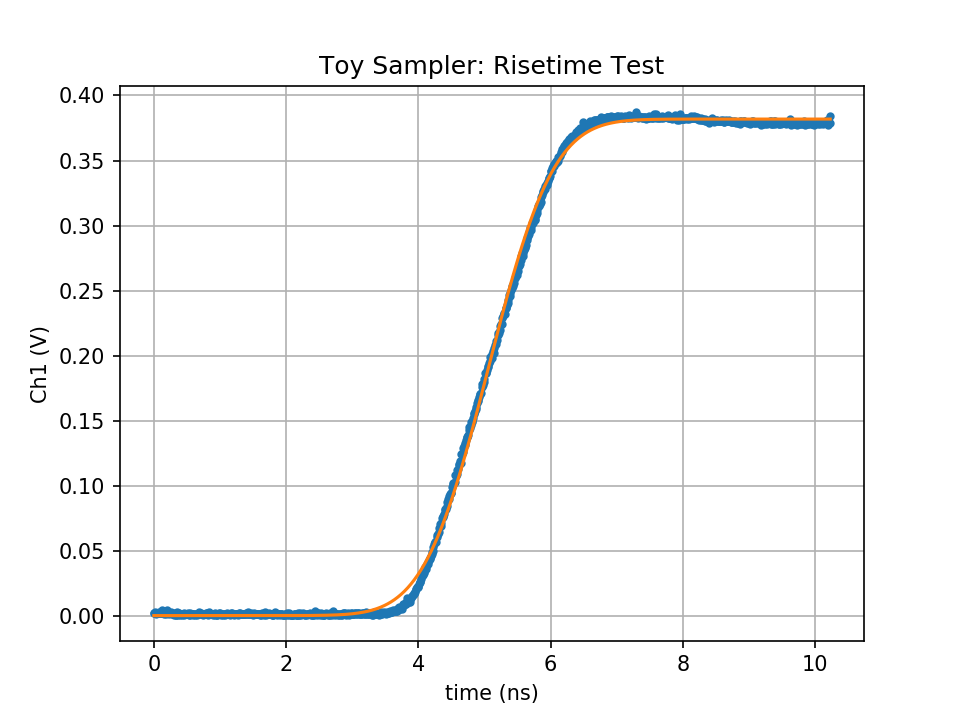
I tested the bandwidth using one of the previous edge generators that manages a modest 666 ps rise time. The resulting measurement has an approximately 1.97 ns measured rise time, which corrected for the rise time of the pulse itself is probably closer to 1.86 ns, from which we can infer a bandwidth of around 188 MHz. I estimated the rise time by least-squares fitting the best Gaussian step to the data (orange line). It's not a bad fit, really. This is probably due to all the errors summing into an approximately Gaussian response. The Central Limit Theorem saves my ass again.

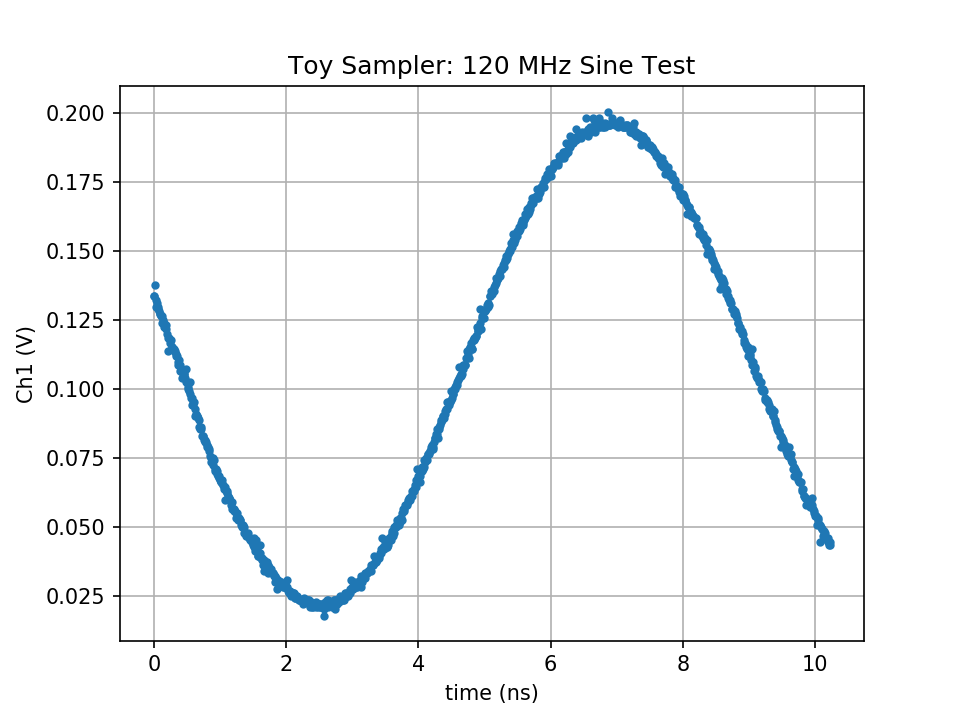
Next, I tried a sine wave. My DDS only goes up to 120 MHz, which looks a little big on this timescale, but still recognizable. The individual samples are around 10 ps apart, although I didn't calibrate the timebase. That's 100 GS/s. Not bad for less than $20 in parts (single quantities).

As a final test, I looked at the output of my DDS set to the fastest edge it can produce, spec'ed at 8.4 ns. To get this trace, I stitched together five separate captures of 10 ns each.

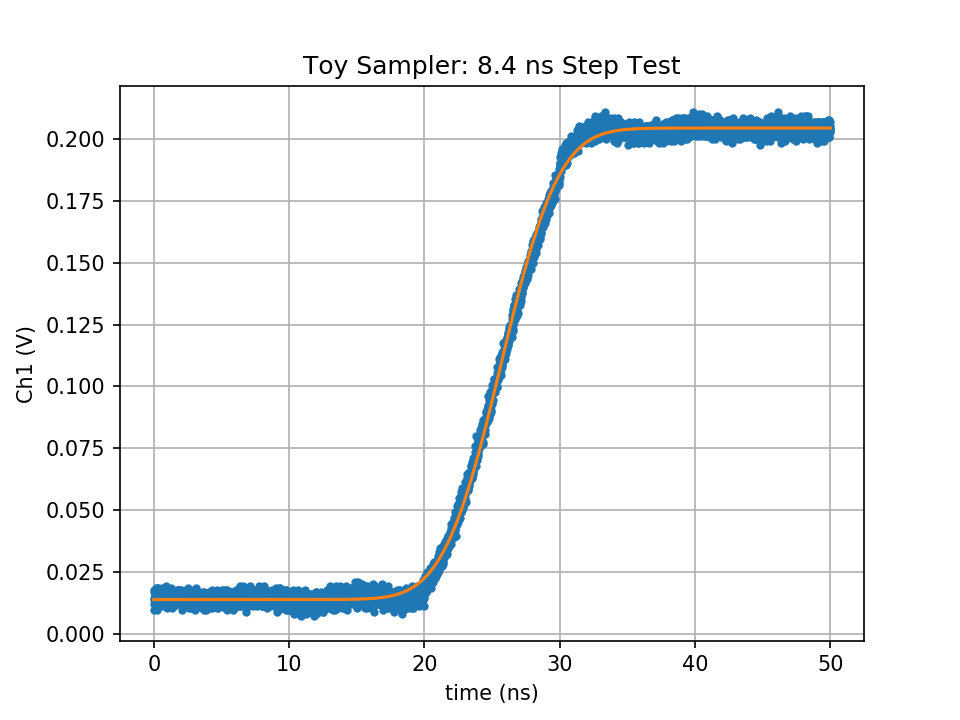
The DDS says the step has an 8.4 ns rise time, but I haven't verified this with a "real" scope. I'll do that next time I'm in the lab. The Gaussian fit works well again on this step, estimating a 8.59 ns rise time. I'll write up how to fit a Gaussian step and estimate rise time from it at some point in the near future.

You can see more noise in these samples, because I used a tighter sampling loop that doesn't let the storage capacitor settle as long. There's a log upcoming about the details.

I'm also not sure how to automatically extend the sweep time like in this example. So far, it's been some trickery involving the DDS, but I really need a general solution. I can cascade the SY89296U programmable delay to give increments of 10.24 ns, but at around $10 each, it would be an expensive way to reach microsecond-length sweeps.

More research is required. And large government grants.