In the previous post, I looked at ways to implement AND, OR and buffers with relays.  But a full logic family requires the ability to invert a value.

With a NC relay this is trivial:

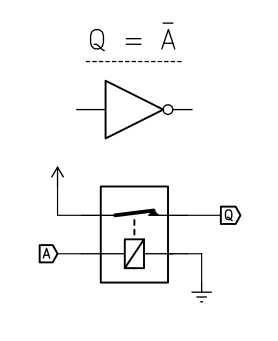
When A is zero, Q is 1.  When current is applied to A, the relay opens and Q becomes logical 0.

This can be extended to produce a NOR gate:

Q is 1 only when A and B are both 0.  

Note how this circuit mirrors the AND gate.  Per DeMorgan's Law, AND is equivalent to NOR with both its inputs inverted.

NAND can also be implemented by mirroring the previous OR gate using NC relays instead.

Negation with Normally-Open Relays:

With a little care, it is also possible to implement negation with a normally-open relay:

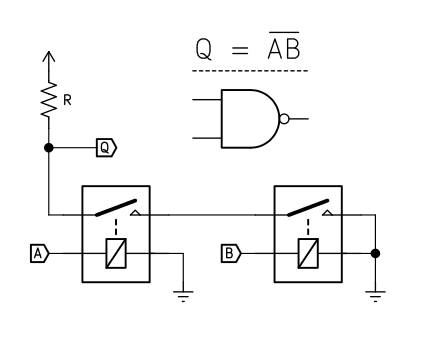
When A is low, Q is pulled up to supply through R.  When A goes high, Q is shorted to ground and goes low.

Note that this gate has some properties different from the previous ones.  First, the output swings between supply and ground, not supply and not connected.  Second, the ability of this gate to drive further gates is limited by the value of R.  Finally, this gate will consume power, dictated by the value of R, every time the input is high, as power flows to ground through it. 

R should be selected as a compromise between current use and ensuring that Q can drive inputs.  Too low a value of R and the gate will draw enormous power whenever the output is low.  Too high and it won't be able to drive any gates itself. 

I suspect it will often be desirable to follow this gate with a regular buffer, to provide isolation, normal supply/NC levels, and higher fan-out.

Despite these drawbacks, this gate does work and it proves that SPST-NO relays are capable of functional completeness.

This can be extended to implement NAND:

As well as NOR:

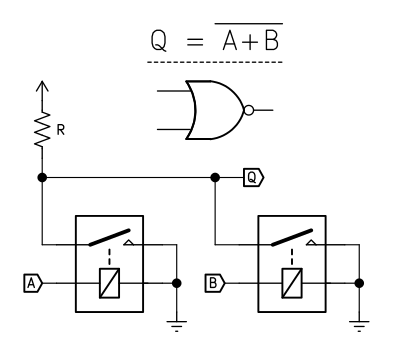
At this point, we have functional completeness and combinatorial and sequential logic can be implemented with these gates.

But that's far from the end of the story.  It's often possible to implement a function with far fewer relays than a naive Boolean equivalent might suggest.  A D-latch normally requires 4 NOR or NAND gates which would be 8 relays.  But I've got a circuit that can do it in just a few relays.  More on that later.