The RGB LED's are a major piece to Weather Color Strip, and mixing of the RGB elements is also important in order to accurately show the color of the temperature outside. The colors are mixed by calculating duty cycles for Red, Green and Blue LED's based on the temperature information parsed from a weather API. The duty cycles are determined using this graphic I have made:
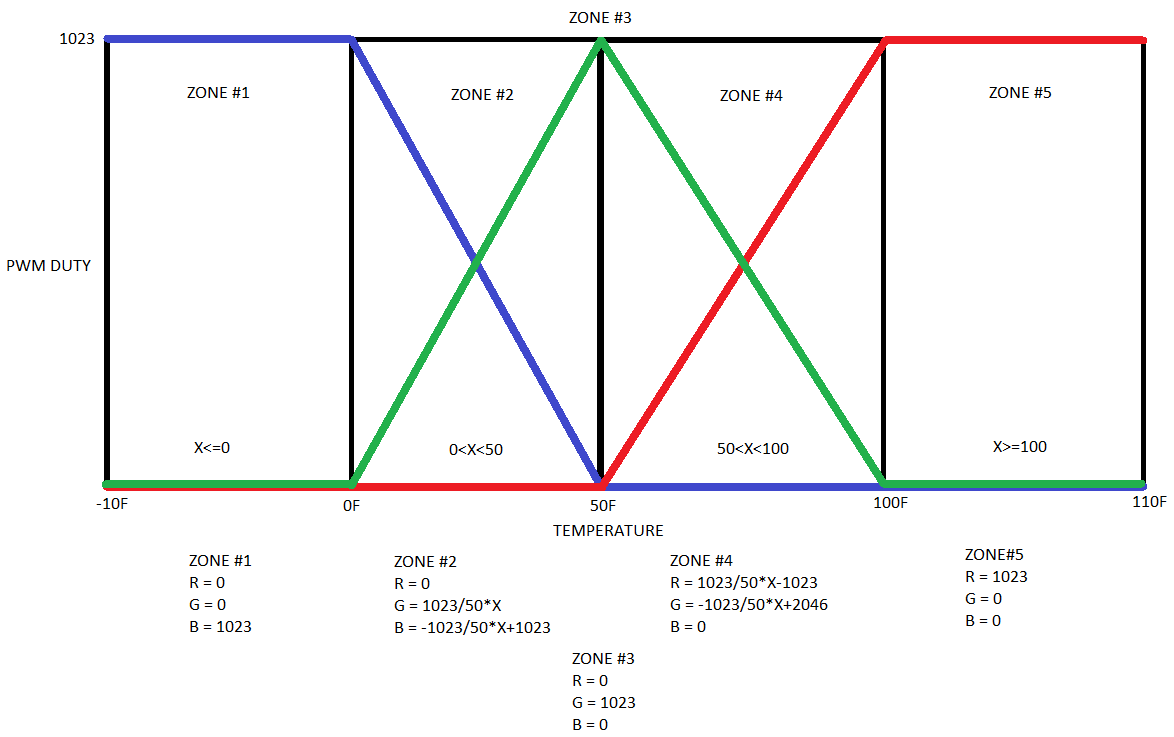
The problem I have noticed is the color spectrum can be green heavy, red heavy or blue heavy depending on the color balancing of the RGB elements. Ideally I would like to see an even spread of blue/green at lower temperature and red/green at higher temperatures. Currently I have tried four different strategies and would like to document the results:
- Equal Resistance
- Each LED (Red, Green and Blue) will have the same current limiting resistor value
- Equal Current
- Each LED (Red, Green and Blue) will have the same current
- Equal Intensity
- Each LED (Red, Green and Blue) will have a scaled max current so each LED will have an equal intensity
- 3:6:1 Color Mixing Ratio
- Create an overall target for intensity. 30% will be red, 60% will be green and 10% will be blue.
The LED's I used are Cree SLV6A-FKB-CK1P1G1BB7R3R3. Digikey page is below:
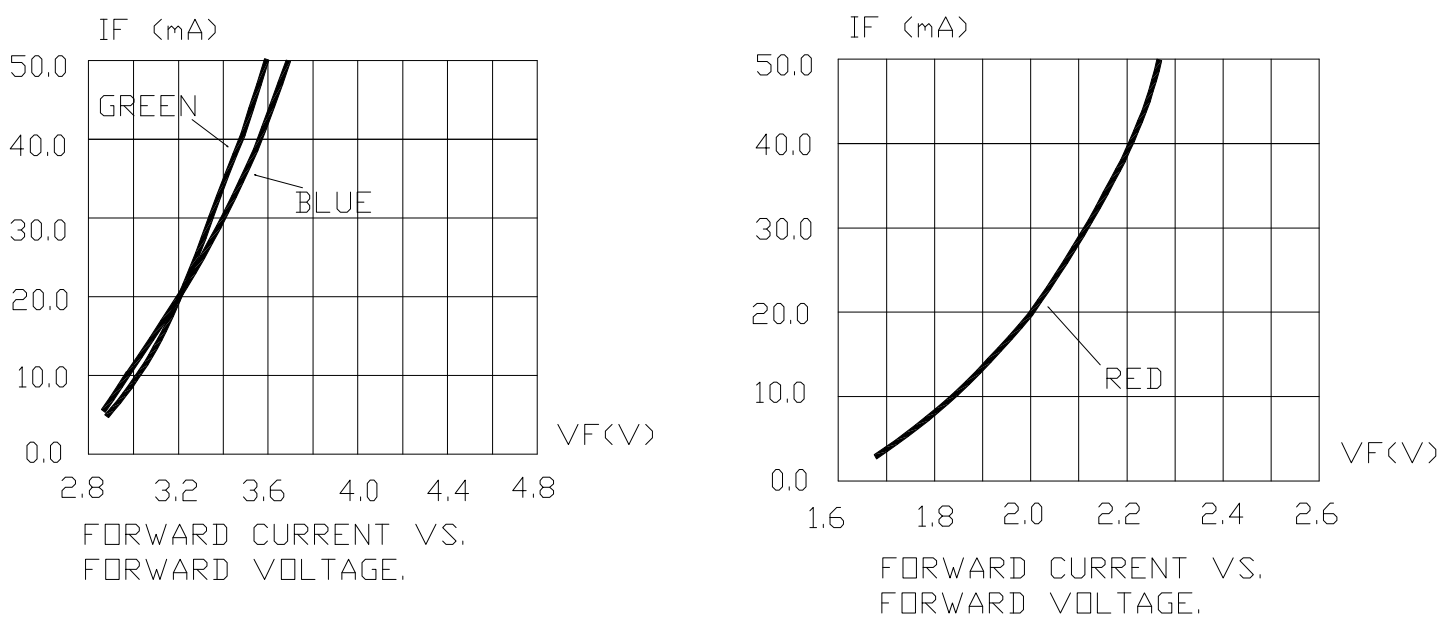
You will notice that the LED voltage drops in each formula are changing slightly. This is change is due to changes in LED current. This voltage drop is very important when calculating ideal LED resistor values. Relationship between LED current and voltage drop can be found in the following graphs:
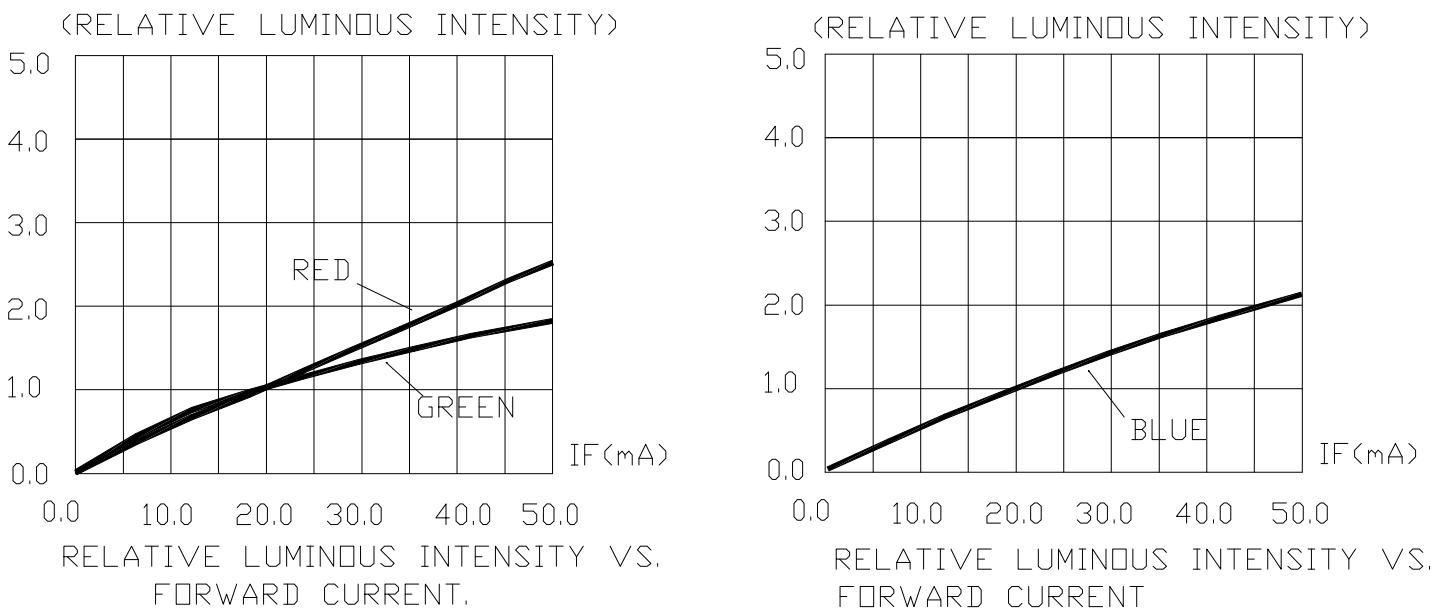
Another important section of the datasheet are the Relative Luminous Intensity curves. These curves show the relationship between current and luminous intensity. These are important when trying to calculation the ideal LED currents:
Equal Resistance
For this strategy I simply used a common resistor values for Red, Green and Blue LED's. I chose a simple 1k resistor.
Actual resistances, currents and intensities are summarized below:
| RED | GREEN | BLUE | |
| RESISTOR VALUE (OHM) | 1000 | 1000 | 1000 |
| LED CURRENT (mA) | 10.16 | 9.000 | 9.050 |
| INTENSITY (mcd) | 355.6 | 960.000 | 181.000 |
Equal Current
For this strategy I tried to make the LED current for Red, Green and Blue to be 10mA. Below is some math on how I calculated the LED resistor values:
| RED | GREEN | BLUE | |
| RESISTOR VALUE (OHM) | 1000 | 887 | 887 |
| LED CURRENT (mA) | 10.16 | 10.124 | 10.169 |
| INTENSITY (mcd) | 355.6 | 1079.895 | 203.382 |
Equal Intensity
For this strategy I tried to scale each LED current in order to have the same intensity for each LED (Red, Green and Blue). I was trying to achieve a target intensity of 400mcd. Using the Relative Luminous Intensity curves, I figured out how much current each LED would need in order to achieve 400mcd. Below is some tables/math on how I calculated the LED resistors values:
| RED | GREEN | BLUE | |
| 20mA INTENSITY (mcd) | 700 | 1600 | 400 |
| RELATIVE INTENSITY (@ 400mcd) | 0.571 | 0.250 | 1.000 |
| REQUIRED LED CURRENT (mA) | 11.429 | 5 | 20 |
I have calculated the necessary current values to achieve 400mcd of intensity. Now I can perform similar calculations completed in the equal current strategy to calculate resistor values:
Actual resistances, currents and intensities are summarized below:
| RED | GREEN | BLUE | |
| RESISTOR VALUE (OHM) | 887 | 2430 | 442 |
| LED CURRENT (mA) | 11.342 | 3.745 | 19.910 |
| INTENSITY (mcd) | 396.956 | 399.451 | 398.190 |
3:6:1 Color Mixing Ratio
This strategy involves having specific intensity ratios for red, green and blue LED's. The ratio is 30% red, 60% green and 10% blue. I do not have a ton of information where this ratio came from, I simply found it by doing searches on the topic of color balancing with RGB LED's. My overall intensity target for the RGB LED is 1500mcd. I have calculated the necessary intensities for each LED (red, green and blue) and used the Relative Luminous Intensity curves from before to calculate the required LED current for those specific intensities. Below are the results:
| RED | GREEN | BLUE | |
| 3:6:1 MIXING RATIO | 30% | 60% | 10% |
| 3:6:1 MIXING RATIO INTENSITY (mcd) | 450 | 900 | 150 |
| 20mA INTENSITY (mcd) | 700 | 1600 | 400 |
| RELATIVE INTENSITY (@ 400mcd) | 0.643 | 0.563 | 0.375 |
| REQUIRED LED CURRENT (mA) | 12.857 | 8.438 | 7.5 |
I have calculated the necessary current values to achieve these specific intensities. Now I can perform similar calculations completed in the equal current strategy to calculate resistor values:
Actual resistances, currents and intensities are summarized below:
| RED | GREEN | BLUE | |
| RESISTOR VALUE (OHM) | 787 | 1070 | 1210 |
| LED CURRENT (mA) | 12.859 | 8.421 | 7.554 |
| INTENSITY (mcd) | 450.064 | 898.193 | 151.074 |
Testing
I built 4 different sets of RGB LED strips with each strategy. Taking pictures of each condition will allow us to compare the color profile of all 4 strategies side by side. Below are all RGB responses from 0F to 100F at 10F increments:
0F (Red Duty = 0%, Green Duty = 0% & Blue Duty = 100%)
| EQUAL RESISTANCE | EQUAL CURRENT | EQUAL INTENSITY | 3:6:1 COLOR MIXING |

10F (Red Duty = 0%, Green Duty = 20% & Blue Duty = 80%)
| EQUAL RESISTANCE | EQUAL CURRENT | EQUAL INTENSITY | 3:6:1 COLOR MIXING |

20F (Red Duty = 0%, Green Duty = 40% & Blue Duty = 60%)
| EQUAL RESISTANCE | EQUAL CURRENT | EQUAL INTENSITY | 3:6:1 COLOR MIXING |

30F (Red Duty = 0%, Green Duty = 60% & Blue Duty = 40%)
| EQUAL RESISTANCE | EQUAL CURRENT | EQUAL INTENSITY | 3:6:1 COLOR MIXING |

40F (Red Duty = 0%, Green Duty = 80% & Blue Duty = 20%)
| EQUAL RESISTANCE | EQUAL CURRENT | EQUAL INTENSITY | 3:6:1 COLOR MIXING |

50F (Red Duty = 0%, Green Duty = 100% & Blue Duty = 0%
| EQUAL RESISTANCE | EQUAL CURRENT | EQUAL INTENSITY | 3:6:1 COLOR MIXING |

60F (Red Duty = 20%, Green Duty = 80% & Blue Duty = 0%)
| EQUAL RESISTANCE | EQUAL CURRENT | EQUAL INTENSITY | 3:6:1 COLOR MIXING |

70F (Red Duty = 40%, Green Duty = 60% & Blue Duty = 0%)
| EQUAL RESISTANCE | EQUAL CURRENT | EQUAL INTENSITY | 3:6:1 COLOR MIXING |

80F (Red Duty = 60%, Green Duty = 40% & Blue Duty = 0%)
| EQUAL RESISTANCE | EQUAL CURRENT | EQUAL INTENSITY | 3:6:1 COLOR MIXING |

90F (Red Duty = 80%, Green Duty = 20% & Blue Duty = 0%)
| EQUAL RESISTANCE | EQUAL CURRENT | EQUAL INTENSITY | 3:6:1 COLOR MIXING |

100F (Red Duty = 100%, Green Duty = 0% & Blue Duty = 0%)
| EQUAL RESISTANCE | EQUAL CURRENT | EQUAL INTENSITY | 3:6:1 COLOR MIXING |

All On (White) (Red Duty = 100%, Green Duty = 100% & Blue Duty = 100%)
| EQUAL RESISTANCE | EQUAL CURRENT | EQUAL INTENSITY | 3:6:1 COLOR MIXING |

Conclusion
All 4 strategies had noticeable RGB mixing result differences. Some I like more than others, but I feel like there is a combination of all that may work out best. Below is a breakdown of my assessment for each strategy:
- Equal Resistance
- The simplest of the strategies design wise, and had excellent results. I love the spread of colors on the low range of temperature (Blue/Green), but I feel the high end of temperatures (Red/Green) are a bit Green heavy.
- I think maybe adjust the green and blue currents down equally may maintain the lower temperature response that I like, while reducing the green effect at higher temperatures.
- Equal Current
- Very similar to equal resistance. I feel like this strategy is even more green heavy at higher temperatures (Green/Red)
- Equal Intensity
- This strategy seems extremely Blue heavy at lower temperatures (Blue/Green). This is even more apparent during the all on white test.
- I really like the higher temperature (Red/Green) spread.
- 3:6:1 Color Mixing
- Overall i think this might have the best response. I feel like the higher temperatures (Red/Green) are a bit more "bright".
Long story short, I dont really know which is best, but I thought the best way to learn would be to experiment with a few different strategies.
Please let me know your thoughts, or if you have some knowledge on the best way to approach RGB mixing ratios. I am sure this is slightly different for every RGB LED, but it seems to be a great area to learn more.
Hope you enjoyed. Thanks.
 schwarzrmsu
schwarzrmsu
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
Nice discussion. Thanks. I am starting to play with FASTled and wondering about these color renderings. I assume (correct me if I am wrong) the following:
Newton used a prism to split white light into a rainbow of color. You want to associate outside temperature to color. Cold to blue, hot to red. It looks like color mixing is the way to go. But the 80deg color mixing does not look too good. (Just saying...)
Maybe you are not using programmable RGB light strips? And have to play games with resistors. I am betting the "perfect" resistor choice for, say, pure yellow is not the correct resistor choice for pure blue. If you did use programmable LED's you could do a specific setting for exactly the color you want at each temperature.
If you have not looked at LED strips with independently programmable colors, do so. It's completely astonishing how they work. The Arduino library FASTled and demo programs are neat. I recommend NOT diving into how the driver works or you will get a headache. Stay at the "user level" for a (long) while.
I think I will have to do something like the 3:6:1 stuff as I start to play more. The human visual system sure is weird.
--jim
Are you sure? yes | no
Wow! I am designing an RGB led right now and was curious how to tune the intensities and here you've made a very helpful blog post just a few days ago. Just one question, why does the image for equal intensities at white setting look purple?
Are you sure? yes | no
Great question, and I wish I had a great answer. This is partly why I did this experiment because I was unsure which strategy would work best.
I figured equal intensities would yield the best esults, but this strategy gave off a very "blue heavy" response. Meaning there wasnt a great range of color between 0F & 50F, it was more or less just blue. This means when you turn everything on, the blue shows up prodominatley in the white test.
Therefore I would have to guess the intensities are equal to a piece of test equipment, but not to the human eye. I am curious if we perceive blue more intensly than the other colors, hence why this 3:6:1 mixing ratio strategy works out well.
Also this might make sense why the LED manufacturer deliberatly provides intensities very close to this 3:6:1 ratio when each LED element has the same current. This is also probably why I got good results for equal current and equal resistance.
Long story short is I have some learning to do myself. If you learn something please feel free to leave another comment to help me out.
Thanks.
Are you sure? yes | no