Goal

The goal of this task is to evaluate the best model for a discrete component object recognition system.

The first task would be to obtain a reference. Typical MNIST classifiers are well below 5% error rate (https://en.wikipedia.org/wiki/MNIST_database#Classifiers). We'll use a reference random forest, with no pre-processing on our reduced dataset.

Benchmark model

The dataset was reduced using the tools shown in https://hackaday.io/project/170591/log/175172-minimum-sensor and evaluated using the same metrics from the previous task.

Training the Random Forest does tax the system quite significantly. The training of a 10k dataset using parallel processing consumed all 8 cores of my laptop at full blast for a good few minutes.

The resulting random forest has the following characteristics:

• 500 trees
• Accuracy 83.6%

Considering that:

• The pixel density used was 4 x 4, instead of 28x28; and,
• Only 10k records were used and there was no pre-processing on the data, the fit is OK.

The fit for individual values was good and most digits were over 80%.

        0         1         2         3         4         5         6         7         8         9 
0.8257426 0.8731284 0.9075908 0.8347743 0.8348018 0.8653367 0.9028459 0.8548549 0.7389061 0.7337058 

Our aim is to make a model, based on decision trees, that could be implemented using discrete components that should match the accuracy of the random forest model.

Decision tree models

The choice of decision trees is due to the simplicity of this model with regards to its later implementation using discrete components.

Each split on a decision tree would take into account a single pixel and evaluated using discrete components.

By tuning the complexity parameters, we can increase the complexity of the tree in order to try and fit a decision tree that will approach the accuracy of the random forest.

The table below shows the effect on accuracy of the cp parameter:

      cp      Accuracy
 0.0010000000 0.6921987
 0.0005000000 0.7162860
 0.0003333333 0.7295383
 0.0002500000 0.7375396
 0.0002000000 0.7389565
 0.0001666667 0.7412902
 0.0001428571 0.7423737
 0.0001250000 0.7422904
 0.0001111111 0.7422904
 0.0001000000 0.7411235

The default cp parameter for the rpart package in R is 0.01 and with successive iterative reduction we obtain no visible increase in accuracy with cp below 0.00025 and we're still quite a way away from the target accuracy obtained with the random forest.

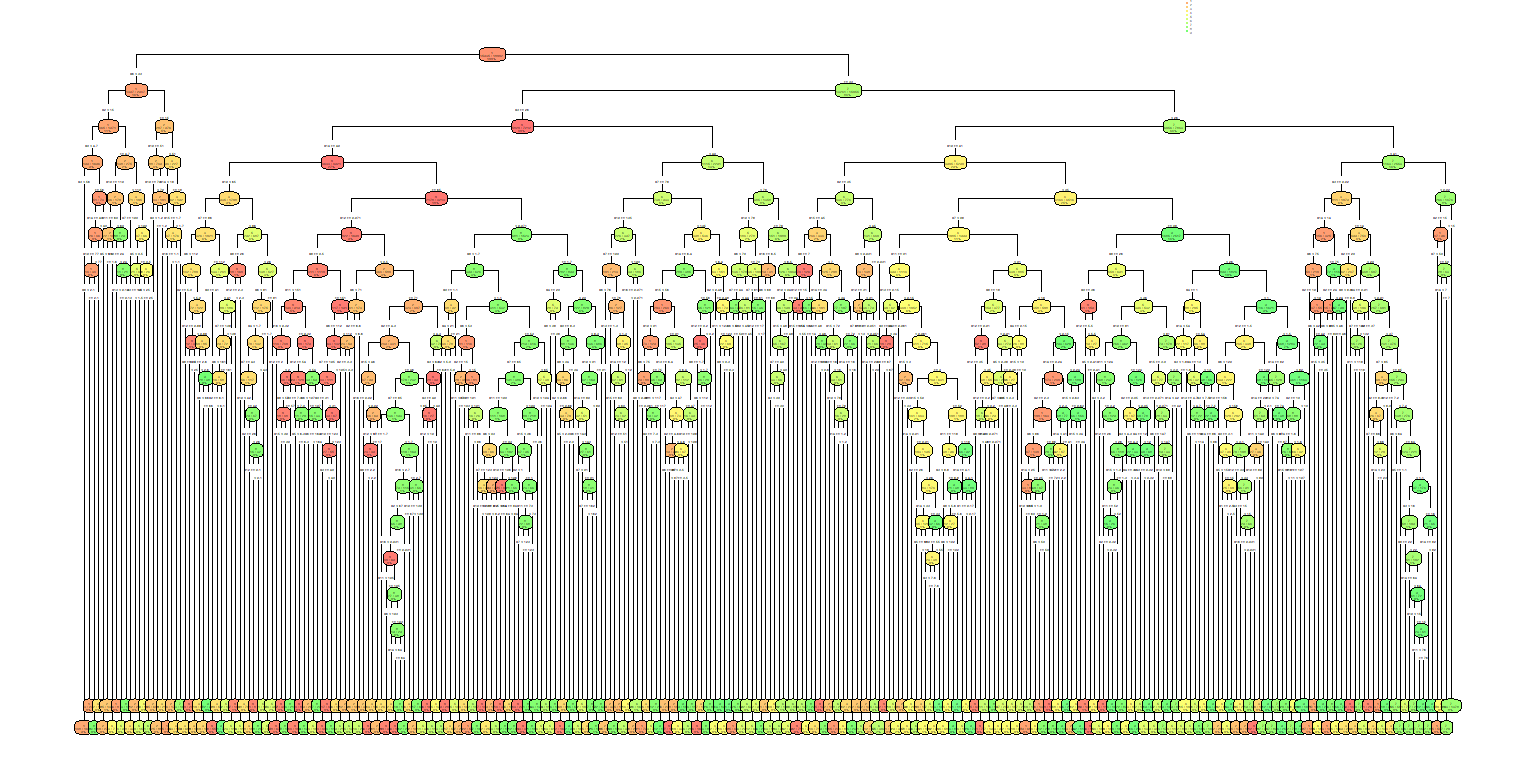
Even settling for a cp of 0.0025, assuming there's a limit on what can be achieved with decision trees, the result is mindboggling. The resulting tree has a total of 300 nodes or splits.

Could it be implemented using discrete components? Definitely. Maybe.

Conclusion

Decision trees can achieve a reasonable accuracy at recognizing the MNIST dataset, at a complexity cost.

The resulting tree can reach a 73% accuracy which is just shy of the 75% target we set out in this project.