The goal of this task is to train the simplest neural network that could recognise digits from the MNIST database and make it compatible with a discrete component implementation.
Minimum Model Neural Network
This one is an easy one. The simplest neural network (NN) is one with just the inputs and the outputs, with no hidden layer.
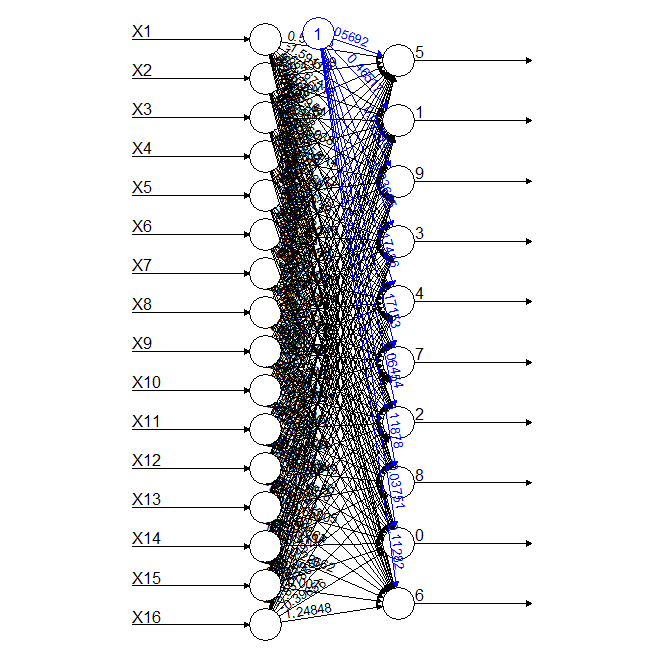
This neural network has a total of 16 inputs which represent the pixels on the 4x4 matrix described in the Mimimum sensor log and 10 outputs representing the 10 digits or classes.
The confusion matrix for this model can be found below.
0 1 2 3 4 5 6 7 8 9
0 768 58 17 17 8 3 75 8 195 17
1 0 1240 6 14 43 14 6 13 7 13
2 26 91 708 61 57 0 171 28 63 5
3 51 134 109 737 20 11 18 127 23 35
4 4 94 13 0 592 6 112 95 27 191
5 109 71 2 45 120 303 111 99 174 31
6 42 45 44 0 95 11 945 2 26 2
7 6 70 8 11 26 2 7 989 1 119
8 45 189 19 34 16 20 61 30 656 102
9 12 103 14 6 110 4 20 387 25 498
The accuracy of the model was not bad, especially when compared with the decision tree or random forest models trained in the previous tasks.
0 1 2 3 4 5 6 7 8 9
0.5256674 0.5608322 0.4909847 0.5072264 0.3634131 0.2667254 0.5270496 0.4876726 0.3829539 0.2939787
Some numbers don't fare well at all, but let us not forget this is a 4x4 matrix, even I couldn't tell the image below belonged to a 0.
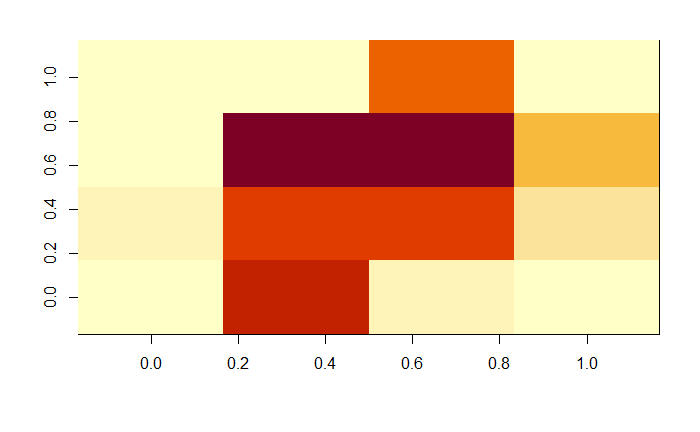 Of course a higher pixel density will improve the accuracy of the model but I'm more interested for the time being in simplicity at the expense of accuracy.
Of course a higher pixel density will improve the accuracy of the model but I'm more interested for the time being in simplicity at the expense of accuracy.
So this was the simplest NN model I could come up with, so we introduced some complexity to see how much we could improve the accuracy. The first model had a single hidden layer with 16 nodes as shown below together with the accuracy values for each digit.
0 1 2 3 4 5 6 7 8 9
0.5044997 0.6573107 0.5772171 0.5874499 0.4180602 0.5212766 0.6659436 0.4793213 0.4176594 0.3957754
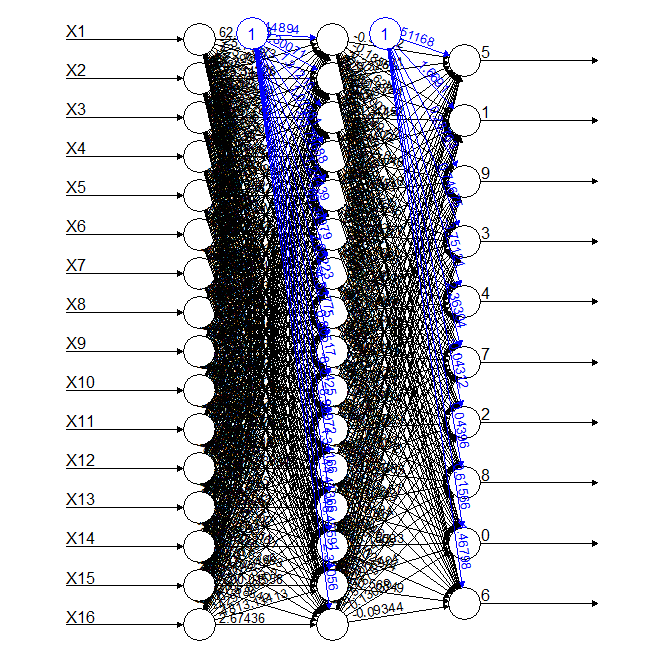
The accuracy increased in some digits, but not so much as to justify the increase in complexity. The second model had two hidden layers with 16 nodes each, as shown below together with the accuracy values.
0 1 2 3 4 5 6 7 8 9
0.4885246 0.7461996 0.5099656 0.4409938 0.4449908 0.4448424 0.6528804 0.5533742 0.3882195 0.2722791
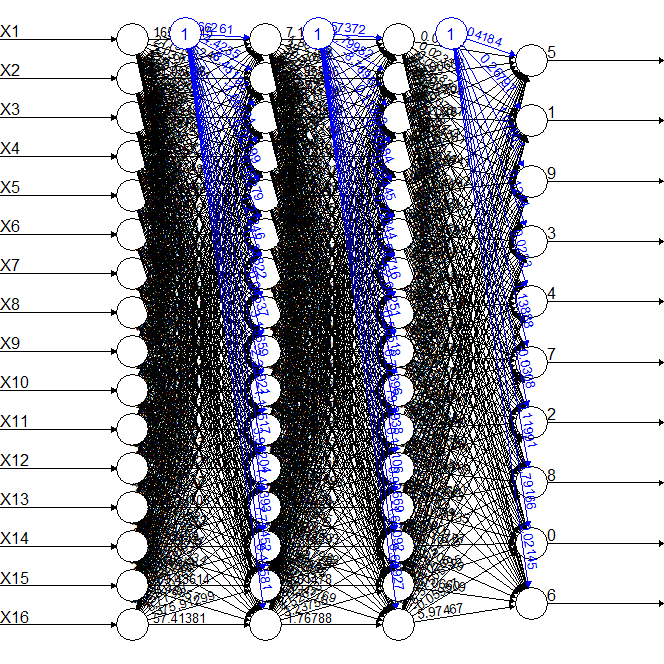
The accuracy of the second model with two hidden layers was better than with one layer, but not for all digits and the cost is realy high in terms of complexity. Overall, the best trade off between complexity and accuracy was the first model.
Breaking down the maths
As neural networks go, they're as simple as they come. The nodes receive the inputs, multiply them by a weight and add a bias. Piece of cake.
The result is then for each node:
That means that knowing the weights and bias of an output node we could in principle calculate its probability with very simple maths.
For example, for the first model shown at the top of the page, the weights for each sensor and the bias for the output node for digit "5" are:
Input Weight Signal Product
1 Bias -0.05691852 N/A -0.05691852
2 Sensor 1 0.5397329 0 0
3 Sensor 2 -0.4359923 0.004321729 -0.00188424
4 Sensor 3 0.3074641 0.2772309 0.08523854
5 Sensor 4 -0.4892472 0.0004801921 -0.0002349326
6 Sensor 5 -0.5862908 0 0
7 Sensor 6 0.231549 0.4101641 0.09497309
8 Sensor 7 -0.0697618 0.4403361 -0.03071864
9 Sensor 8 0.5010364 0.164946 0.08264393
10 Sensor 9 1.150069 0.04017607 0.04620524
11 Sensor 10 0.1367729 0.3277311 0.04482472
12 Sensor 11 -0.3862879 0.3078832 -0.1189315
13 Sensor 12 0.7872604 0.08947579 0.07044075
14 Sensor 13 -0.273486 0.009043617 -0.002473303
15 Sensor 14 0.3749847 0.3589436 0.1345983
16 Sensor 15 0.5307104 0.05786315 0.03070857
17 Sensor 16 -0.8331957 0 0
Total: 0.378472
Multiplying the response array from the sensor and adding the bias I can get the result for digit 5, in this case, 0.378472.
Easy, so now we need to implement this using discrete components.
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.