Wprowadzenie
Członków zespołu podzielono na sześć podzespołów:

Projekt automatycznej skrzyni biegów wykonano przy użyciu środowiska
programowego Autodesk Fusion 360, a jej sterowanie za pomocą Arduino Uno.
Przeprowadzono również symulacje podzespołów, wykonano dokumentację
techniczną i wizualizację (render) projektu.
Konstrukcja
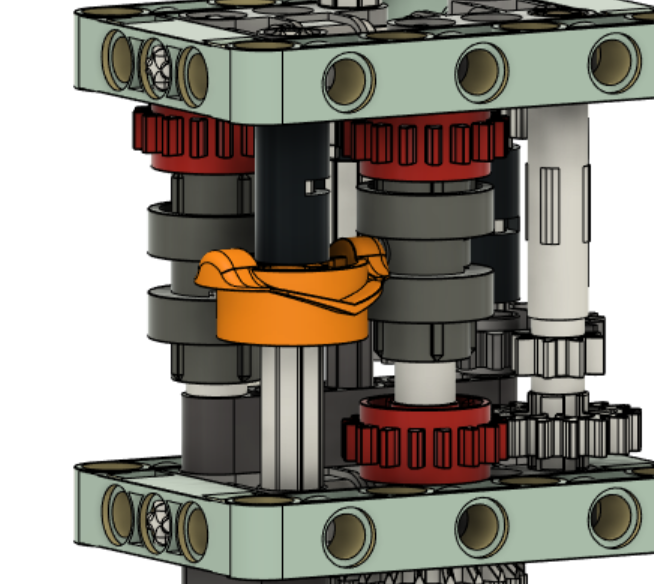
Układ skonstruowany w programie Fusion 360 składa się z modułu do zmiany
biegów, czujnika ultradźwiękowego, silnika LEGO oraz serwa, które służy do zmiany
biegów.
Render modelu - widok z ukosa:

Render modelu - widok z boku:

Render modelu - widok z góry:

Opis działania
Schemat kinematyczny:
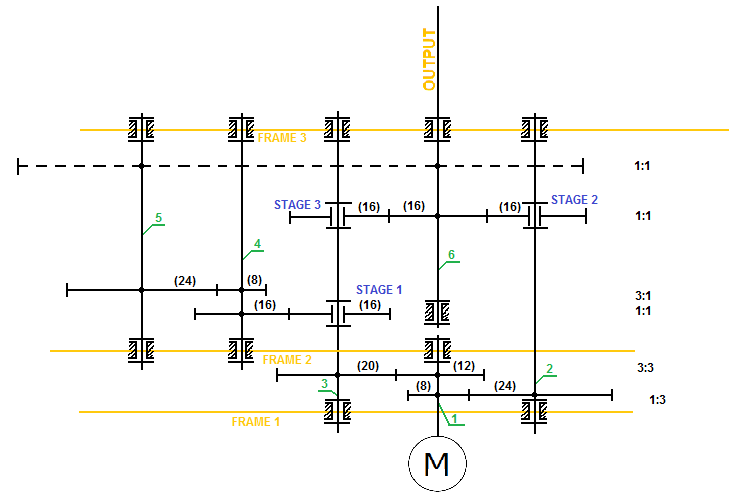
Schemat został zmodyfikowany na rzecz zaprezentowania działania skrzyni na płaszczyźnie 2D. W wyniku czego linią przerywaną narysowano elementy fikcyjne, gdzie w rzeczywistości zamiast nich znajduje się jedno koło (16). Działanie automatycznej skrzyni biegów opiera się na utwierdzaniu z osią odpowiedniego koła obrotowego w wyniku czego uzyskujemy odpowiedni bieg.
Biegi są zmieniane na podstawie elementu podobnego do mechanizmu krzywkowego:
Wizualizacja działania wykonanego projektu automatycznej skrzyni biegów:
Analiza kinematyczna
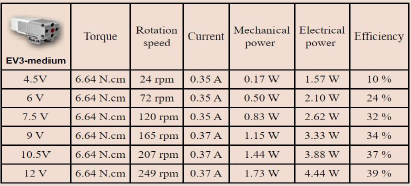
Dane techniczne silnika LEGO EV3 medium motor:
masa = 39 [g]
Parametry w stanie nieobciążonym (dla 9 [V] DC):
n = 260 [rpm]
I = 80 [mA]
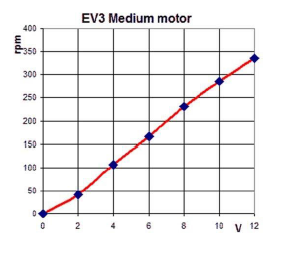
Parametry w stanie przeciążonym (stalled motor) (dla 9 [V] DC):
M = 15 [Ncm]
I = 780 [mA]
Parametry w stanie obciążonym (normalnej pracy):
Kwestia prędkości i momentów poszczególnych osi skrzyni:
Oś 1 jest osią napędową, a oś 6 osią wyjściową (napędzaną).
STAGE 1
Istotne osie o numerach 3, 4, 5.

Ostatecznie na wyjściu mamy:

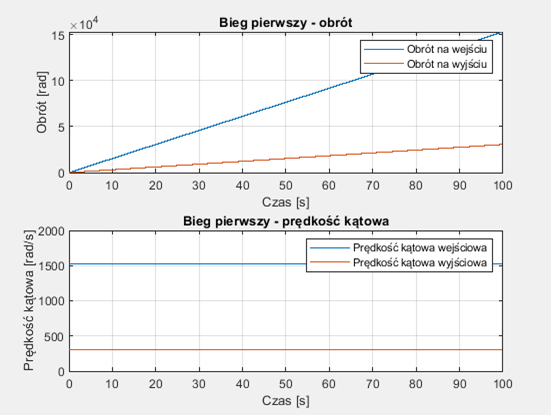
Wykresy prędkości kątowej i obrotu dla biegu pierwszego:
STAGE 2
Istotna oś 2.

Ostatecznie na wyjściu mamy:

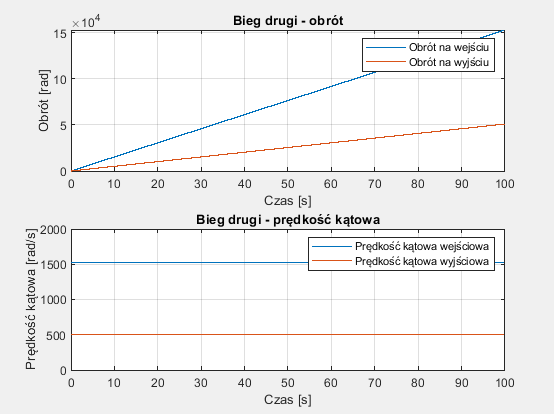
Wykresy prędkości kątowej i obrotu dla biegu drugiego:
STAGE 3
Istotna oś 3.

Ostatecznie na wyjściu mamy:

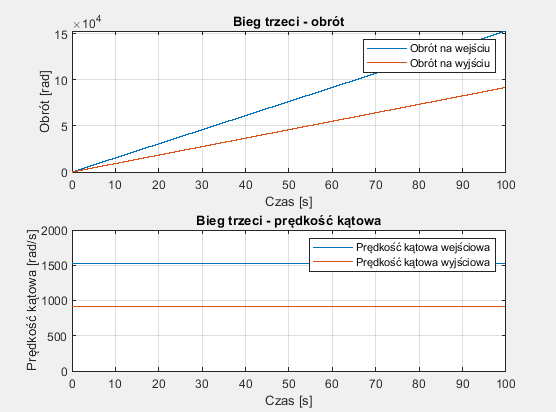
Wykresy prędkości kątowej i obrotu dla biegu trzeciego:
Analiza kinematyczna została przeprowadzona dla każdego biegu z osobna w postaci animacji (stage 1, 2 i 3) oraz wykresów obrotu i prędkości wejściowej od wyjściowej, które zostały wygenerowane za pomocą poniższego pliku Matlaba:
%% Kinematyka skrzyni biegów
clc; clear all; close all;
%wektor czasu
t=0:0.001:100;
%prędkość kątowa na wejściu (dobrana ze specyfikacji silnika (część o
%numerze 9455) z napięciem 9 [V] na wejściu silnika)
w=160*60/(2*pi);
w_in=w*ones(1,length(t));
fi_in=w.*t;
%% Bieg pierwszy
%przełożenie obliczone analitycznie
I1=1/5;
%wykresy wartości kinematycznych, wartości te są wyznaczone analitycznie,
%ale z dobrą dokładnością w praktyce, jako że połączenia kształtowe mają
%dość wysoką sprawność (około 99%)
figure(1);
subplot(2,1,1);
plot(t,fi_in,t,I1*fi_in);
xlabel('Czas [s]');
ylabel('Obrót [rad]');
legend('Obrót na wejściu','Obrót na wyjściu');
title('Bieg pierwszy - obrót');
grid on;
subplot(2,1,2);
plot(t,w_in,t,I1*w_in);
xlabel('Czas [s]');
ylabel('Prędkość kątowa [rad/s]');
legend('Prędkość kątowa wejściowa','Prędkość kątowa wyjściowa');
title('Bieg pierwszy - prędkość kątowa');
grid on;
ylim([0,2000]);
%% Bieg drugi
%przełożenie obliczone analitycznie
I2=1/3;
%wykresy wartości kinematycznych, wartości te są wyznaczone analitycznie,
%ale z dobrą dokładnością w praktyce, jako że połączenia kształtowe mają
%dość wysoką sprawność (około 99%)
figure(2);
subplot(2,1,1);
plot(t,fi_in,t,I2*fi_in);
xlabel('Czas [s]');
ylabel('Obrót [rad]');
legend('Obrót na wejściu','Obrót na wyjściu');
title('Bieg drugi - obrót');
grid on;
subplot(2,1,2);
plot(t,w_in,t,I2*w_in);
xlabel('Czas [s]');
ylabel('Prędkość kątowa [rad/s]');
legend('Prędkość kątowa wejściowa','Prędkość kątowa wyjściowa');
title('Bieg drugi - prędkość kątowa');
grid on;
ylim([0,2000]);
%% Bieg trzeci
%przełożenie obliczone analitycznie
I3=3/5;
%wykresy wartości kinematycznych, wartości te są wyznaczone analitycznie,
%ale z dobrą dokładnością w praktyce, jako że połączenia kształtowe mają
%dość wysoką sprawność (około 99%)
figure(3);
subplot(2,1,1);
plot(t,fi_in,t,I3*fi_in);
xlabel('Czas [s]');
ylabel('Obrót [rad]');
legend('Obrót na wejściu','Obrót na wyjściu');
title('Bieg trzeci - obrót');
grid on;
subplot(2,1,2);
plot(t,w_in,t,I3*w_in);
xlabel('Czas [s]');
ylabel('Prędkość kątowa [rad/s]');
legend('Prędkość kątowa wejściowa','Prędkość kątowa wyjściowa');
title('Bieg trzeci - prędkość kątowa');
grid on;
ylim([0,2000]);
Analiza MES
Z powyższego oraz ze schematu kinematycznego wynika, że osiami najbardziej obciążonymi są osie 2, 5 i 6, stąd dla nich dokonano analizy statycznej w stanie przeciążenia (stalled motor). Założono zasilanie silnika napięciem 9[V].
Badania dla obciążeń w pracy normalnej
Badania zostały przeprowadzone dla osi 2 i 5, które były najbardziej obciążone:
Oś 2:

Oś 5:

Z przeprowadzonej powyżej analizy wynika, że powyższe osie zostały
obciążone:
‐oś 2 ‐ 3‐krotnością momentu wejściowego
‐oś 5 ‐ 5‐krotnością momentu wejściowego
Wały wykonują ruch obrotowy, a przyłożone do nich siły są zmienne, gdyż zmienia
się moment obrotowy na wejściu. Działają na nie również momenty skręcające pochodzące od tarcia między zębatkami przenoszącymi moment obrotowy między
wałami. Na zębatki działają natomiast momenty ścinające.
Dla poszczególnych osi przeprowadzono symulacje w Fusion 360, uzyskane wyniki opublikowano w serwisie Youtube, a także wygenerowano raport html. Poniżej przedstawiono klatki z wykonanych animacji:
Symulacja MES dla obciążeń w pracy normalnej dla osi 2:
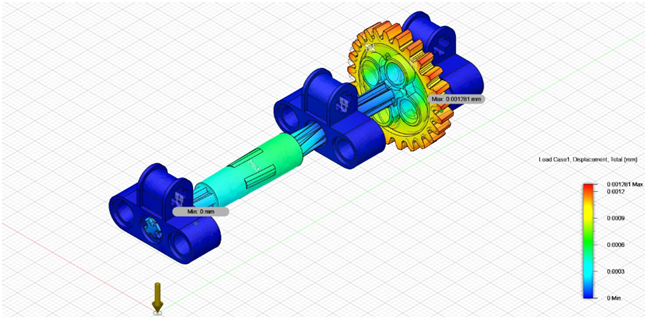
Symulacja MES dla obciążeń w pracy normalnej dla osi 5:

Wygenerowano z Fusion 360 rezultaty analizy dla osi 2 i 5 w formie raportu HTML, który znajduje się w załącznikach.
Podsumowując, po przeanalizowaniu uzyskanych wyników, do uszkodzeń w pracy normalnej może dochodzić na końcówkach zębów, lecz są to wartości niewielkie będące na granicy błędu przeprowadzonej metody.
Badania dla obciążeń w pracy krytycznej
Badania zostały przeprowadzone ponownie dla osi 2, 5 i dodatkowo dla 6, które były najbardziej obciążone.
Poniżej przedstawiono oś 6, będącą osią wyjściową, do której dołożono koło zębate w celu przyłożenia momentu:

Z przeprowadzonej powyżej analizy wynika, że powyższe osie zostały obciążone:
-oś 2 - 3-krotnością momentu wejściowego
-oś 5 - 5-krotnością momentu wejściowego
-oś 6 - 5-krotnością momentu wejściowego
Dla powyższych osi przeprowadzono symulacje w Fusion 360, uzyskane wyniki opublikowano na Youtube, a także wygenerowano raport html. Poniżej przedstawiono klatki z wykonanych animacji.
Symulacja MES dla obciążeń w pracy krytycznej dla osi 2:

Symulacja MES dla obciążeń w pracy krytycznej dla osi 5:

Symulacja MES dla obciążeń w pracy krytycznej dla osi 6:

Wygenerowano z Fusion 360 rezultaty analizy w formie raportu HTML dla osi 6, 2 i 5, który znajduje się w załącznikach.
Po przeanalizowaniu uzyskanych wyników, do uszkodzeń w pracy krytycznej dojdzie dla osi 2. Aby temu zapobiec, nie można doprowadzić do sytuacji, w której oś pracuje pod obciążeniami krytycznymi. Poniżej przedstawiono, gdzie występuje miejsce największych naprężeń dla danej osi ulegającej zniszczeniu:
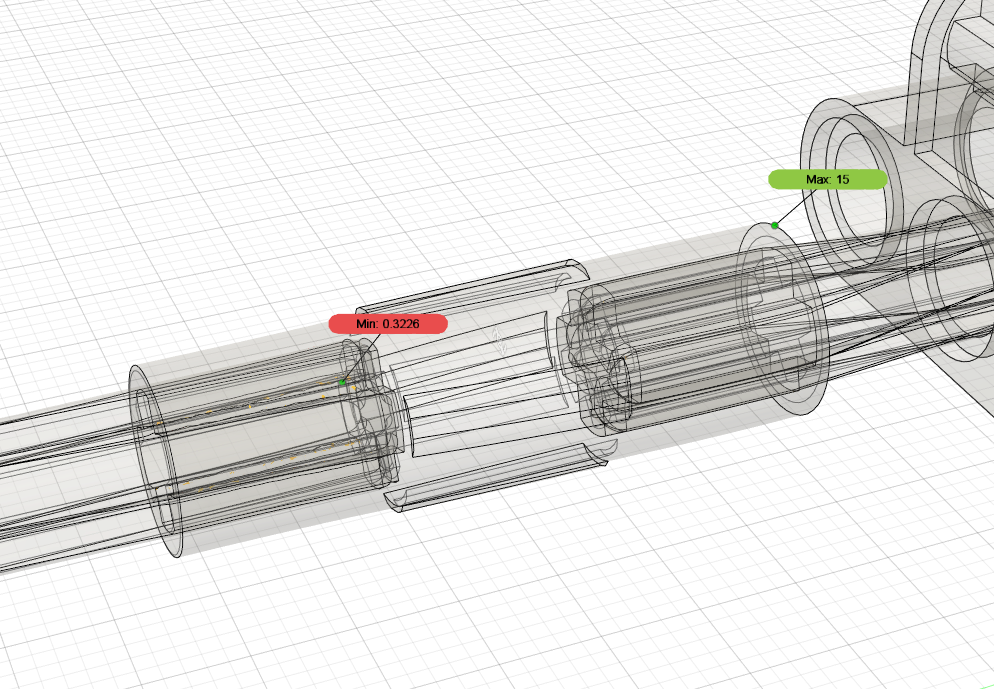
Analiza częstotliwości modalnych
Badania zostały przeprowadzone dla jednego elementu mechanizmu będącego zębatką:

Powyższy element został wprowadzony w drgania za pomocą momentu równego 750 [Nmm]. Poniższy rysunek przedstawia uzyskaną mapę naprężeń spowodowaną danym obciążeniem:

Wygenerowano z Fusion 360 rezultaty analizy dla zębatki, które zostały zapisane w formie raportu html, który znajduje się w załącznikach.
Według przeprowadzonej analizy wynika, że wibracje, w które wchodzi zębatka nie przeszkadzają jej w normalnej pracy, a wynikające z tego uzyskane odkształcenia nie są duże.
Kolizje
Badania zostały przeprowadzone dla poniższej zębatki:

Powyższy element został uderzony z prędkością 10 [m/s]. Poniższy rysunek przedstawia uzyskaną mapę naprężeń spowodowaną danym uderzeniem:

Wygenerowano z Fusion 360 rezultaty analizy w formie raportu HTML dla powyższej zębatki, który znajduje się w załącznikach.
Podsumowując, z przeprowadzonej analizy wynika, że dla uderzenia z prędkością równą 10 [m/s] na uszkodzenia najbardziej są narażone są końce zębów. Jednak mimo tego, zębatka nie powinna ulec zniszczeniu i spowodować zaburzenie pracy mechanizmu.
Symulacje MES dla automatycznej skrzyni biegów zamieszczone w serwisie Youtube:
Sterowanie
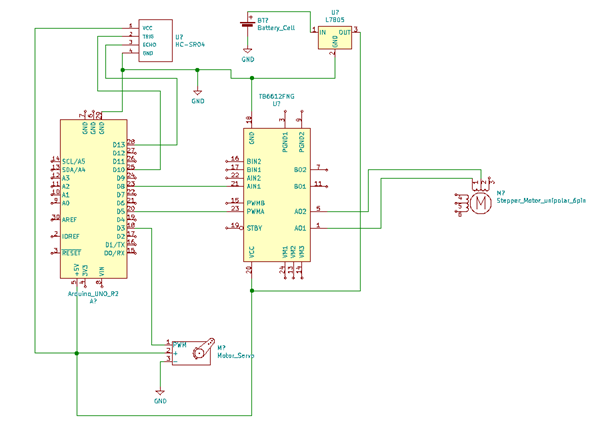
Automatyczna skrzynia biegów sterowana jest za pomocą Arduino Uno. Do mikrokontrolera został dopięty dodatkowy moduł do sterowania silnikiem, aby umożliwić sterowanie jego prędkością obrotową.
Sterowanie opiera się o odczyty z czujnika ultradźwiękowego, który wykrywa wystający z końca wału klocek. Jeśli prędkość kątowa klocka osiągnie wartość krytyczną, bieg zostaje zmieniony. Prędkość kątowa jest liczona poprzez zliczanie ilości obiegów głównej pętli programu pomiędzy kolejnymi pełnymi obrotami wału, a następnie ta wartość mnożona jest razy 0.1 (ponieważ każdy obieg pętli ma zapisane opóźnienie 10 mikrosekund).
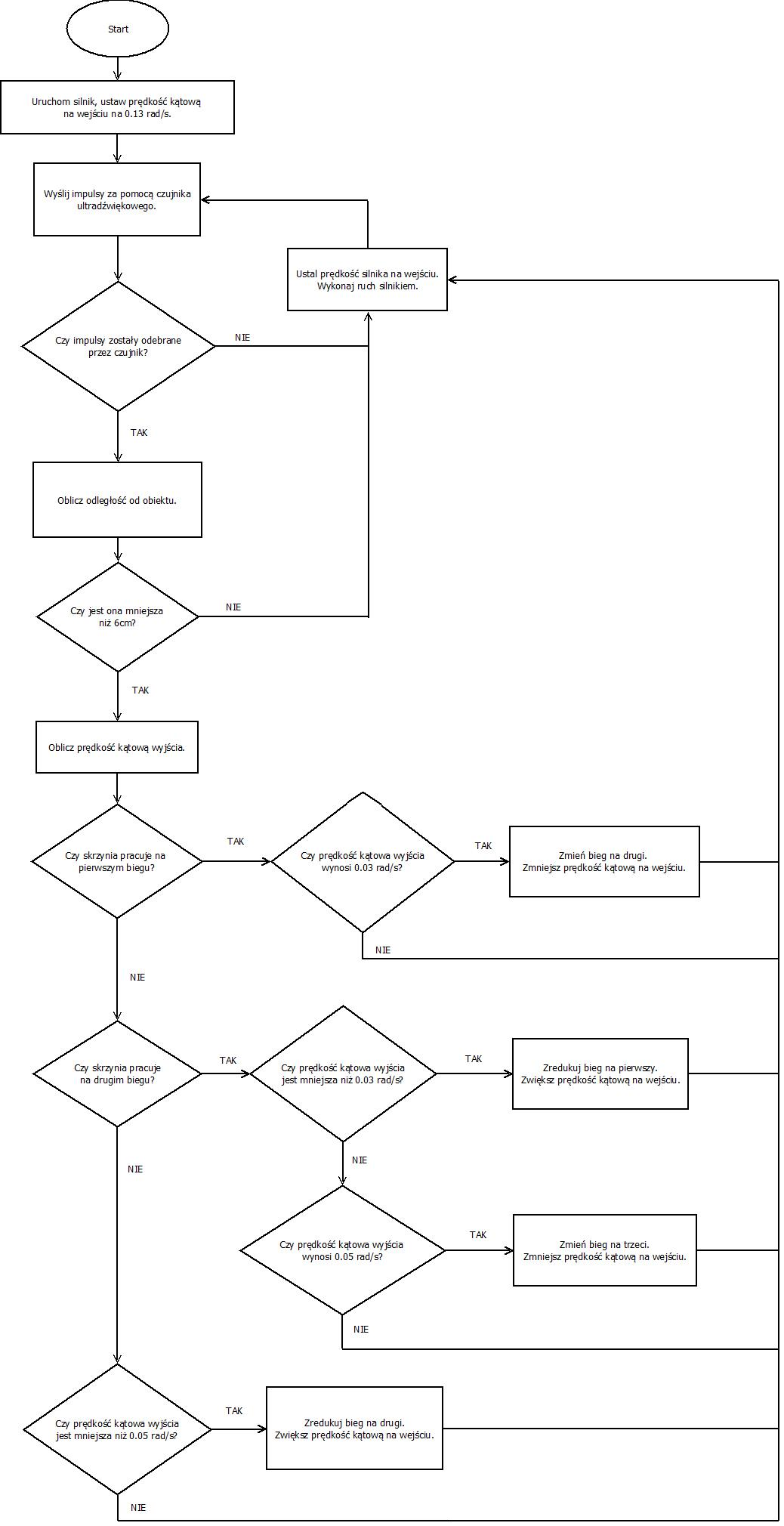
Po uruchomieniu silnika jego prędkość kątowa na wejściu zostaje ustawiona na 0.13 [rad/s]. Za pomocą czujnika ultradźwiękowego wysyłane są impulsy. Gdy impulsy nie są odbierane przez czujnik, zostaje ustalona prędkość silnika na wejściu, wykonywany jest jego ruch i ponowne wysłanie impulsów i sprawdzenie czy impulsy są przez niego odbierane. W przypadku twierdzącym obliczana jest odległość od obiektu. Sprawdzany jest warunek, czy jest ona mniejsza od 6 [cm]. Jeśli nie, ustalona zostaje prędkość silnika na wejściu, wykonany ruch silnikiem i kolejne następujące czynności jak poprzednio. Dla spełnionego warunku obliczona zostaje prędkość kątowa wyjścia. Jeśli skrzynia pracuje na pierwszym biegu, to sprawdzony zostaje warunek, czy prędkość kątowa na wyjściu wynosi 0.03 [rad/s] i jeśli tak, to bieg zostaje zmieniony na drugi, a prędkość kątowa na wejściu jest zmniejszana. Dla problemu przeciwnego ustalona zostaje prędkość silnika na wejściu i wykonany jest jego ruch. Dla przypadku gdy skrzynia pracuje na drugim biegu zostaje sprawdzone, czy prędkość kątowa wyjścia jest mniejsza niż 0.03 [rad/s] i wtedy bieg jest redukowany do pierwszego i prędkość kątowa na wejściu zostaje zwiększona. Gdy odpowiedź jest negatywna, zostaje sprawdzone, czy prędkość kątowa wyjścia wynosi dokładnie 0.05 [rad/s] i jeśli tak, to następuje zmiana biegu na trzeci i zmniejszenie prędkości kątowej na wejściu. Dla problemu przeciwnego ustalona zostaje prędkość silnika na wejściu i wykonany jest jego ruch. Jeśli skrzynia nie pracuje na biegu pierwszym lub drugim, sprawdzony zostaje warunek, czy prędkość kątowa wyjścia jest mniejsza niż 0.05 [rad/s]. Dla odpowiedzi pozytywnej bieg zostaje zredukowany na drugi i jest zwiększana prędkość kątowa na wejściu, a dla negatywnej ustalana jest prędkość silnika na wejściu i wykonywany jest jego ruch.
Algorytm sterowania
Schemat podpięcia elementów układu
Układ rzeczywisty
Stworzono również rzeczywisty układ, który zaprezentowano na poniższym zdjęciu:

Ze względu na brak czujnika ultradźwiękowego LEGO został on zastąpiony przez czujnik HC-SR04. Do układu rzeczywistego nie zostało dołączone również serwo odpowiadające za zmianę biegów, co jest wynikiem braku jego dostępności.
Skrypt:
#include
//Ultrasonic Sensor
int trigPin = 10;
int echoPin = 13;
//Motor
int PWMA = 5; //speedcontrol
int AIN1 = 8;
//Servo
Servo ServoSensor;
int servoPin = 3;
int first_gear = 0;
int second_gear = 90;
int third_gear = 180;
int mtrSpeed = 200, gear = 1;
int i = 0, x = 0;
float w = 0, v = 0;
int currentState = 0, previousState = 0;
float duration, distance;
void setup()
{
Serial.begin(115200);
pinMode(trigPin, OUTPUT);
pinMode(echoPin, INPUT);
pinMode(PWMA, OUTPUT);
pinMode(AIN1, OUTPUT);
ServoSensor.attach(servoPin);
ServoSensor.write(0);
}
voidloop()
{
digitalWrite(trigPin, LOW);
delay Microseconds(2);
digitalWrite(trigPin, HIGH);
delay Microseconds(50);
digitalWrite(trigPin, LOW);
duration = pulseIn(echoPin, HIGH);
distance = (duration/2)*0.0343;
w = i*0.1;
x = x+1;
if (distance< 6)
{
if (currentState == 0)
{
currentState = 1;
i = i+1;
}
else
{
previousState = 1;
i = i + 1;
}
}
else
{
currentState = 0;
previousState = 0;
i = i+1;
}
delay(10);
if (gear == 1)
{
if(currentState != previousState && w > 15)
{
v = 1/(i*0.1);
Serial.println(1/(i*0.1));
i = 0;
}
if(v == 0.03)
{
gear = 2;
ServoSensor.write(second_gear);
mtrSpeed = mtrSpeed * (3/5);
x = 0;
}
}
else if (gear == 2)
{
if(currentState != previousState && w > 15)
{
v = 1/(i*0.1);
Serial.println(1/(i*0.1));
i = 0;
}
if(v < 0.03)
{
gear = 1;
ServoSensor.write(first_gear);
mtrSpeed = mtrSpeed * (5/3);
x = 0;
}
else if(v == 0.05)
{
gear = 3;
ServoSensor.write(third_gear);
mtrSpeed = mtrSpeed * (1.6/3);
x = 0;
}
}
else
{
if(currentState != previousState && w > 9)
{
v = 1/(i*0.1);
Serial.println(1/(i*0.1));
i = 0;
}
if (v < 0.05)
{
gear = 2;
ServoSensor.write(second_gear);
mtrSpeed = mtrSpeed * (3/1.6);
x = 0;
}
}
if(x > 1000)
{
mtrSpeed = mtrSpeed + 10;
x = 0;
}
boolean inPin1 = HIGH;
boolean inPin2 = LOW;
digitalWrite(AIN1, inPin1);
analogWrite(PWMA, mtrSpeed);
}