Last time we set up the compiler environment. I'm using it extensively now and works great. I only had a few times where the bootloader did not start the image after sending it over serial (and then I had to reset it and send the image again, so no drama).

I decided to start out by using the '34-sounddevices' sample project, because it looks like it's really simple to modify it, and get it to play sound data instead of a 440hz tone.

So my idea is to add sound data to the project, so that I can patch it in to where the 440hz tone is fed into the buffer. I'm really in unfamiliar territory here, but have heard of the double buffering pattern. I think that's what the original author does here. We have an audio buffer of a fixed length, and then there is a loop that will fetch data from this buffer, and write parts of it to the audio device's output buffer. We are supposed to write data to the first buffer, so that the loop can write it to the second. The reason behind this is to prevent audio dropouts. Basically by having two audio buffers, we make sure that the strictly timed audio device always has data, even if the timing of the processing/generation code is not that strict. Audio is something that is very time sensitive. Much like a video plays at 30 frames per second, cd-quality audio (wow that's been a while since I called it that) needs 44100 samples per second (times two if you want stereo output).

If you're already experienced with how sound works in bits and bytes, I suggest you skip the rest of this log, as it really only explains the fundamentals, no advanced processing (yet).

Now let's talk about what a sample actually is. Before starting this project, I had a vague representation in my head of how a sample is stored in computer memory. But diving deeper into this, I picked up a few things.

So let's get it out of the way; sound consists out of waves. A wave goes up and down. Depending on how loud it is, the wave goes higher. But like I said, a wave goes up and down. When it goes down, it still goes louder. This is called the amplitude. It's an audio waves thing, if this sounds weird to you, I suggest you look up on information how sound reproduction works, like say how a speaker reproduces sound.

A computer does not store waves, it stores bits. So, how can a computer then store a wave? By taking samples from it. Samples are points in time where the amplitude of a wave are measured. And for cd-quality audio, for every second 44100 points are measured.

There is a good image on wikipedia that illustrates this, every point on the wave is a sample:

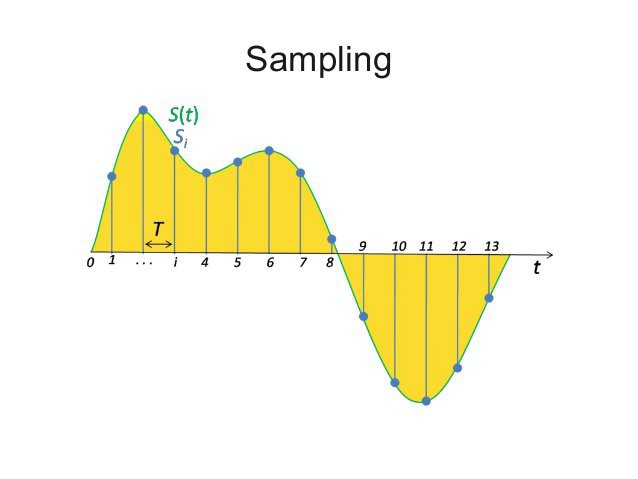
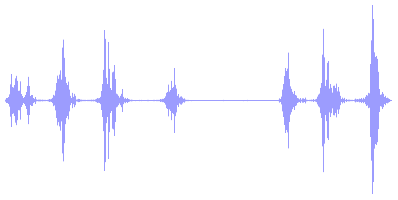
For the time being, assume we're talking about 1 channel (so mono, not stereo). When your audio is stored as 8-bit, your computer offers you an array of 44100 bytes for each second of audio that represent the loudness of those parts of the wave. The bytes represent time sequentially, so byte 22050 contains a sample of the wave at 0.5 seconds in time. So every byte is 1 sample. The midpoint of a wave is silence. In the illustration from wikipedia above, the midpoint is represented by the line in the middle. The image below illustrates this a little bit better because its shows you a longer waveform over time, you may say it's 'zoomed out' compared to the illustration from wikipedia above, which is heavily 'zoomed in'.

In 8-bit audio the midpoint is 127. So silence is represented by 127. That is ... when we are talking about 8-bit audio. For those of you who lived and played games in the MS DOS era, 8-bit audio just sounds yuck. CD-quality audio is 16-bit. And in 16-bit you have the choice to see your samples represented as a signed or unsigned integer. In case you wonder, a 'signed' integer is a number that can go below zero. Knowing that, when using a 16-bit signed integer, the highest amplitude (a.k.a. loudness) a sample can have is 32767 and -32767, and so 0 equals silence. On the other side, if audio is stored as a 'unsigned' 16-bit integer, the highest amplitude is 0 and 65535, where 32767 is the midpoint and equals silence. You see, the result is exactly the same, it's just a different way of storing the data. As a human, I like the signed representation, because that aligns with the way my brain thinks. Wave goes up: number is positive, wave goes down: number is negative, wave is center (so, complete silence): number is 0. Using signed integers for samples also makes doing math on them a lot easier. Spoiler alert: later on we'l discover that converting the signed integers to floating point data for processing is the ultimate way.

Now that we know this, we can start manipulating samples using maths! Yeeey! If you read the previous log, maybe you'll remember me saying that I suck at maths. That hasn't changed. I might even have a mild form of dyscalculia, who knows. That being said, expect calculation mistakes along the way on my part. Don't say I didn't warn you!

Let's see how we can apply that in practice. Suppose we have an 44100hz 16-bit audio buffer called 'Sound' filled with samples. We want to make the first two seconds less loud. We can do this by modifying the amplitude of the samples for the first two seconds by doing this:

for (int s=0; s<88200; s++) {
    Sound[s] *= 0.5;
}

 If you know that there are 44100 samples in a second, then you know that two seconds worth of audio has 88200 samples.

And so our journey has begon in manipulating audio. In the next log I hope to share some project code with you. When learning the information above myself, I already created some filter algorithms that mimic the sound of the mpc1000, so I'm pretty excited to share this with you!