See the beginning at 3. Rewrite as well as 35. Internal Representation in v2.9 for more dirty details !

After a hiatus, it's finally time to work again on the implementation of the algorithm explained in the log 36. An even faster and easier algorithm to map the netlist !

The linear function 5x+3 can be configured to trade off security for speed, with POLY_OFFSET and POLY_FACTOR. The higher the factor, the better the discrimination of snafus, but that increases the number of steps. A generic with default value is appropriate in this case.

The principle of serialising and de-serialising through wire-type symbols is shown in the picture below. The original idea, around 2001, used binary codes for real wires but std_logic provides 8 useful symbols, plus the "refresh" one ('U').

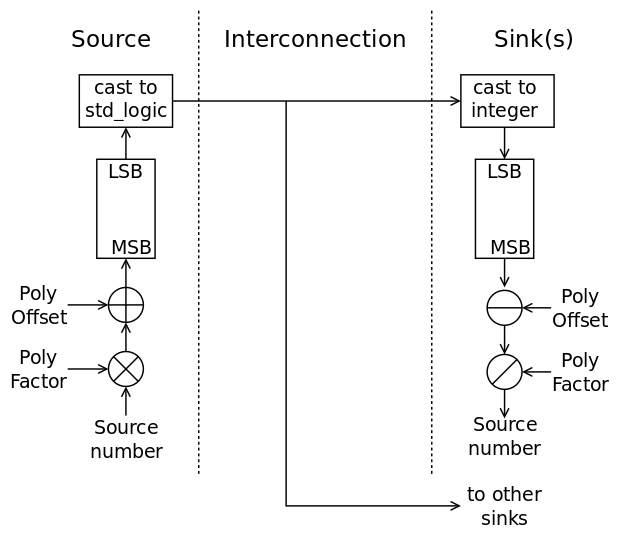
Conversion between integers and the enumerated std_logic type is not as trivial as in other languages but still very easy, when you "get" how to dance around the strong typing constraints, as shown in this code:

Library ieee;
    use ieee.std_logic_1164.all;
entity test_std is
end test_std;

architecture arch of test_std is
begin
  process is
    variable i : integer;
    variable s : std_logic;
  begin
    for j in std_logic'low to std_logic'high loop
      if j = std_logic'high then
         s := 'X';  -- not 'U', to show a custom wrap-around
      else
         s := std_logic'succ(j);
      end if;
      report integer'image(std_logic'pos(j))
            & " : " & std_logic'image(j)
            & " : " & std_logic'image(s);
    end loop;

    for i in 0 to 7 loop
      s := std_logic'val(i+1);
      report std_logic'image(s);
    end loop;

    wait;
  end process;
end arch;

The result:

$ rm -f test_std *.o *.cf && ghdl -a test_std.vhdl && ghdl -e test_std && ./test_std 
test_std.vhdl:24:7:@0ms:(report note): 0 : 'U' : 'X'
test_std.vhdl:24:7:@0ms:(report note): 1 : 'X' : '0'
test_std.vhdl:24:7:@0ms:(report note): 2 : '0' : '1'
test_std.vhdl:24:7:@0ms:(report note): 3 : '1' : 'Z'
test_std.vhdl:24:7:@0ms:(report note): 4 : 'Z' : 'W'
test_std.vhdl:24:7:@0ms:(report note): 5 : 'W' : 'L'
test_std.vhdl:24:7:@0ms:(report note): 6 : 'L' : 'H'
test_std.vhdl:24:7:@0ms:(report note): 7 : 'H' : '-'
test_std.vhdl:24:7:@0ms:(report note): 8 : '-' : 'X'
test_std.vhdl:31:7:@0ms:(report note): 'X'
test_std.vhdl:31:7:@0ms:(report note): '0'
test_std.vhdl:31:7:@0ms:(report note): '1'
test_std.vhdl:31:7:@0ms:(report note): 'Z'
test_std.vhdl:31:7:@0ms:(report note): 'W'
test_std.vhdl:31:7:@0ms:(report note): 'L'
test_std.vhdl:31:7:@0ms:(report note): 'H'
test_std.vhdl:31:7:@0ms:(report note): '-'

So it's pretty trivial to convert an int to std_logic and vice versa. It's a bit less so to extract bit fields from an integer because VHDL does not provide the shift and boolean operators :-( As I have tested a decade ago, going with bitvectors is too slow. The only way is to divide or multiply but the semantic is somehow lost and this does not work correctly with negative numbers (due to inappropriate rounding). I don't want to use my own shift&bool routines because they link to C code and that might break somehow in the future with new revisions to GHDL.

There is also a constraint on the amount of data that can be stored in the descriptor of each gate. For example a complete precomputed std_logic_vector would take too much room and the size would not be easy to determine before running the whole thing.

One compromise could be to store one std_logic element that is precomputed before each new pass. There are already 2 such variables in the record of each gate: curOut and prevOut but then, what about the input gates ?

curOut,                 -- the last result of lookup
prevOut : std_logic;    -- the previous result of the lookup
changes : big_uint_t;   -- how many times the output changed
LUT     : std_logic_vector(0 to 15); -- cache of the gate's LUT.

sinks : sink_number_array(0 to 3);

The variable changes can be used to accumulate the number to serialise, but the LUT can't be overwritten because it's necessary for the following steps of the algorithm.

sinks is an array of numbers that can be used to de-serialise the incoming numbers for each input. Serialisation would start "LSB first" so each new received symbol is simply shifted left, or multiplied, by a variable amount, which is very simple.

-- in the driver :
...
variable multiply_pass : integer := 1;
...
-- don't forget to first clear all
-- the counters in the cells' sinks
...
loop
  -- send the data
  ...
  wait for 1 s;  -- yield to the code in the cells
  ...
  multiply_pass := multiply_pass * 8;
end loop;

-- in the cells :
...
variable v : std_logic; -- the received value
variable n : integer;
...
if v = 'U' then
   output <= 'U';
else
   output <= emit();
   -- de-serialisation:
   n := std_logic'pos(v) - 1; -- 0 <= n <= 7
   n := n * multiply_pass;
   sinks(x) := sinks(x) + n;
end if;

the variable multiply_pass goes from 1 to 8 to 64 to 512 to 2048 etc. and places the new 3 bits at the right position.

Then to check the result in sinks(x):

variable n, m : integer;
...
n := sinks(x) / POLY_FACTOR;
m := sinks(x) - (n*POLY_FACTOR); -- compute the modulo
if m = POLY_OFFSET then
  sinks(x) := n;
  -- now "register" the sink in the linked list
else
  error...
end if;

The harder part is for sending. Variable divisions are slow, divisions by constant powers of two can however be optimised at compile time to shifts. The solution appears to be using local shift registers, or accumulators (decumulators ?), instead of calculating the index/offset every time. The intermediate result is saved for the next step, thus saving some calculations, however all the gates must be updated at the same exact time and as many times, or the shifting would be desynchronised. A local update counter is required for each group of sinks (gates and outputs) and will be compared at the end of the tracing algorithm. Inconsistent counter values would betray unconnected sinks for example.

The new diagram makes the idea clearer, I hope :

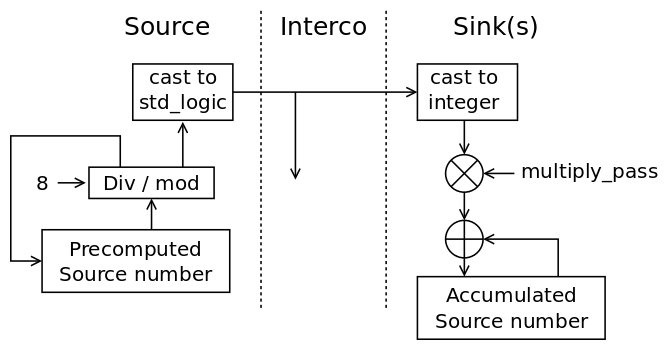
With the fixed div/mod factor, the operation shouldn't be resource-consuming and the list of gates/ports needs only a scan at the start and the end of the loop.

When should the scan loop stop ?

• A safe condition is when all the sources send the same value corresponding to symbol 0.
• When the last serialiser de-cumulator reaches 0

The last one is simpler/shorter and stops earlier than the first so it's adopted :-)

There is a last problem to solve though: the source number must be positive for the transmission algo to work. However negative numbers exist to indicate the input ports... The poly_offset must also include the number of input ports, and start counting from port #0 to DutVectIn_length, then from gate 1 to gate_max (there is no gate #0 !). At this point, backwards gates do not count as input ports.

The algo will :

1. scan to initialise the ports then the gates, incrementing the init value by Poly_factor, and clear the sinks' accumulators.
2. loop and increase multiply_pass, also check the outputs, until the last gate's decumulator reaches 0.
   before letting the gates react, clear a counter, which is incremented by all the gates and output, to ensure that ALL elements receive data at every cycle, ensuring the netlist is fully connected.
3. scan the gates and the outputs, check the sink values' correctness then connecting the sinks to the linked list of the corresponding source.

This should work...