In the last log for the motor controllers used on this robot, I discussed how the motion primitives were updated to roughly match the gait of the MIT Cheetah according to the following video:

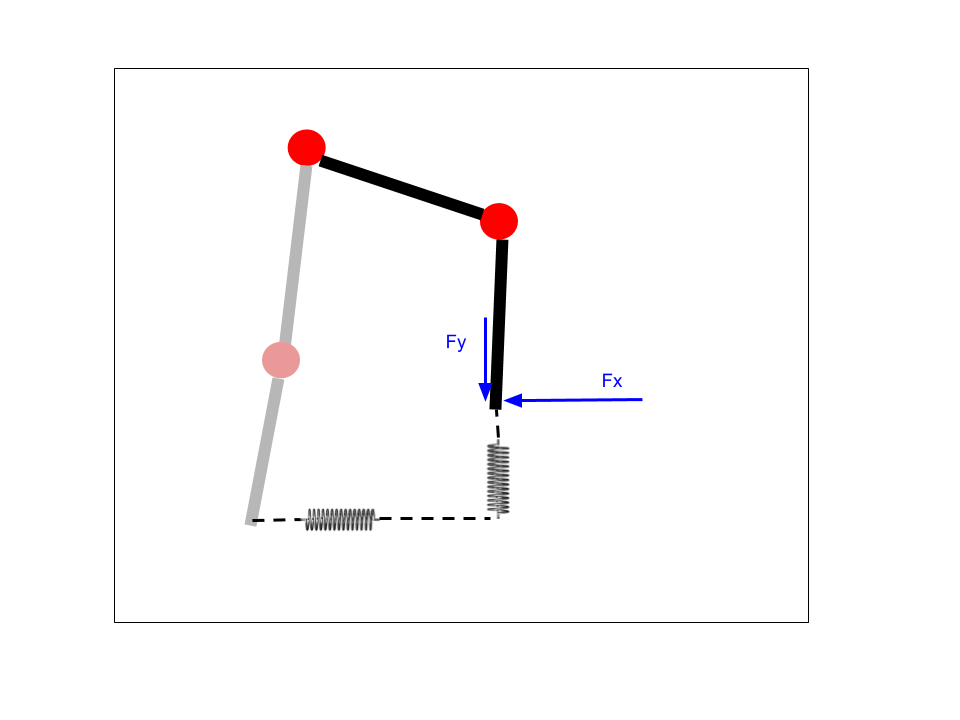
I also noted that my implementation was pretty far from how the MIT Cheetah does its leg motion control. It was different in at least two critical ways. First, while I had 3-4 points in my profiles, and the leg would track between these points according to linear interpolation, the Cheetah uses Bezier curves for smoother motion (or it did at one time per this paper). Second, while my robot tracked those profiles simply using inverse kinematics and position control, the Cheetah is more advanced. Series-elastic actuators have a long history in robotics in helping to stabilize walking motion. The Cheetah uses virtual model control to simulate elasticity in its motion. In the simplest representation of this, consider the image below. Instead of driving the leg to a given position, we instead create a virtual spring (and damper) between a desired point and the foot. The forces that would occur due to this virtual model are calculated, and we drive the hip and knee motors in current, or torque, control mode to achieve this force. Therefore we can think of the foot as being dragged around in space by a virtual spring and damper. Instead of punching the ground with position control, a virtual model controlled leg impacts the ground as if there was an inline spring, and the motion is therefore much smoother. With its high-performance, low gear-ratio brushless motors, the Cheetah is great at doing this. I am using 150:1 gear ratio <$10 brushed motors with single-sided current sensing. Therefore I do not expect nearly as good performance, but I still want to do as best as possible.

Bezier Motion Profiles

Bezier curves are parametric curves defined by a few control points. Various order Bezier curves exist, and in fact linear Bezier curves are simply linear interpolation. Therefore technically I was already using Bezier curves. But clearly motion like that shown below is not smooth.

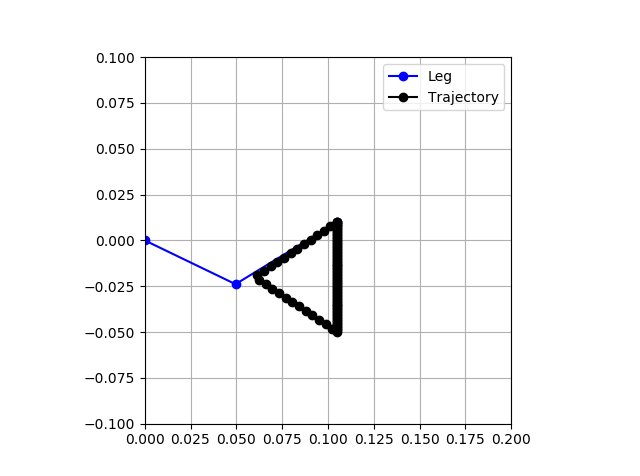
And I do mean smooth in the mathematical sense. The derivative of the curve is discontinuous, which can make for jumpy motion. To keep things a bit simpler, I focused on using quadratic Bezier curves. These also do not ensure mathematically smooth profiles, but by tuning the shape, I can get much smoother motion. In the implementation, we must always have an even number of control points. All even indices (starting at 0) are points that the motion moves through. All of the odd index points "pull" the profile to shape it. Wikipedia has a good explanation on how to generate a quadratic Bezier curve. With this implemented, I regenerated the profile above, but with quadratic Bezier curves and some shaping points. For sanity, I also rotated things so that the leg "down" is down also.

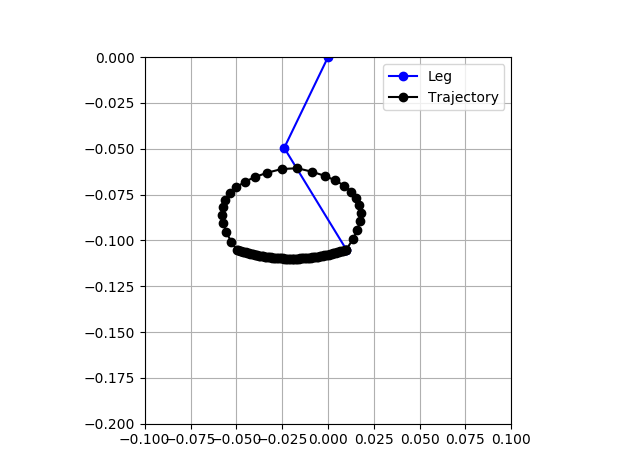
Clearly, this motion will be much smoother and hopefully will result in less jerky walking.

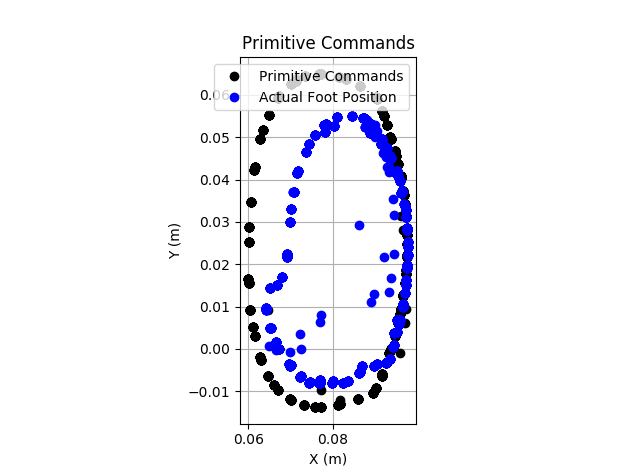
I tested this with position control (virtual model control will be discussed later), and it was successful. This is real test data, with a 2s period. The actual foot positions lag somewhat, but the tracking is overall quite decent.

If we speed up the cycle, it is clear that the motors cannot keep up. At this point it isn't clear if this is a PID tuning issue, or a hardware limitation. This example has a 750ms period, so more than twice as fast.

Virtual Model Control

In one of the logs for the motor controller, I had talked about current control and virtual model control, but did not get great results. I revisited this again, now that I have motion primitives working. I would like to use the Bezier curves along with virtual model control. There are a number of challenges here:

• Depending on the leg orientation, it may not be mathematically possible to generate the desired virtual force front joint torques (think about your leg held out straight with locked knee, now push down...)
• We only have single-sided current sensing, but we want to control current in both directions. This requires care in implementation.
• The motion profiles must be calculated faster than they did for positional control. The motion profile calculations are needed for the current calculations. This was done at 20Hz previously, but that is not fast enough to re-calculate current commands appropriately

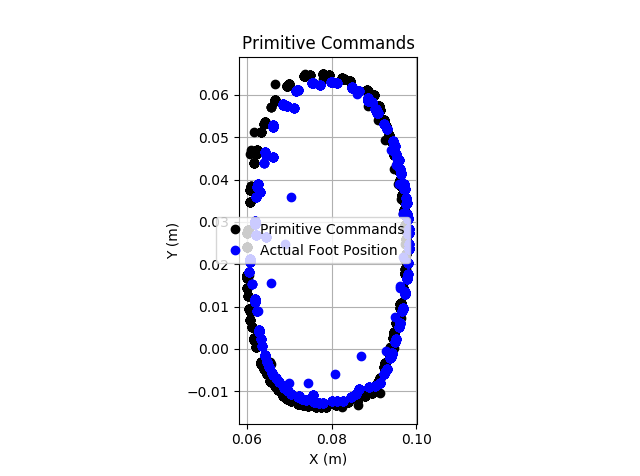
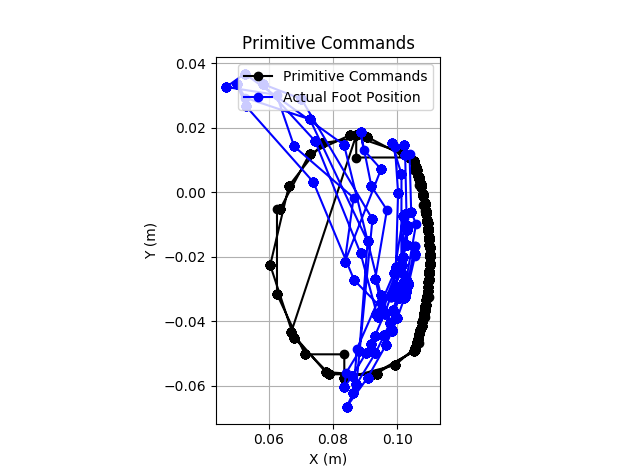
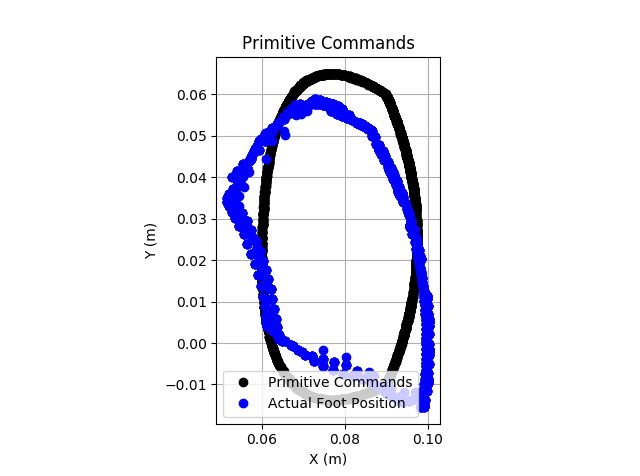
During some of the initial testing, the performance was poor. The image below shows the commanded position per the Bezier curve in black, and the actual foot positions in blue. Clearly it is not tracking well.

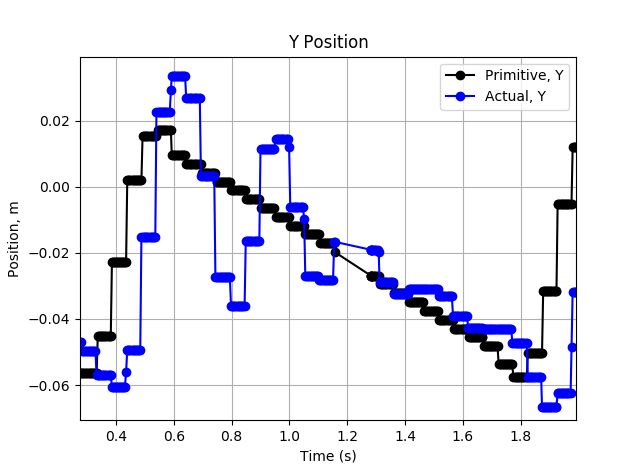
However, there are some promising signs. It is difficult to tell in the image above, but the positional tracking is actually __somewhat__ working. The image below shows the Y-axis tracking over a single cycle. There is clear damped oscillation about and tracking of the desired Y position profile.

At this point, the primitives calculations were still at 20Hz. After increasing that rate to 100Hz, tuning the virtual model, motor model, current PID loops, and more, I was making progress, but results were still a bit odd. The image below shows a typical response. The actual foot position looks more like a banana than the proper Bezier curve.

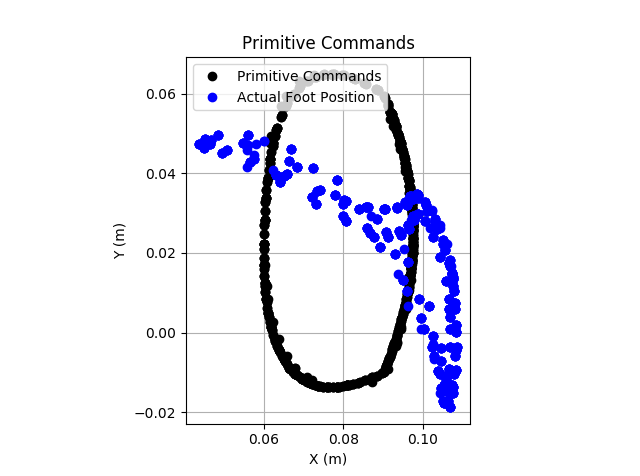
The tracking on the Y-axis actually wasn't too bad here, although there is a strange dip near the peak.

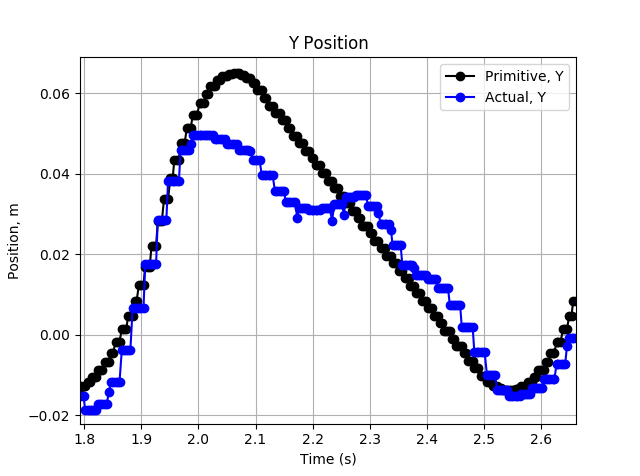
The X-axis tracking however, is quite poor. There is significant lag, overshoot, and undershoot. This is the main cause for the poor tracking.

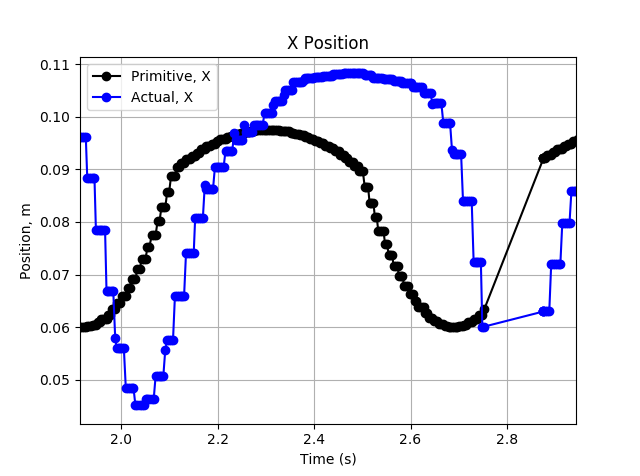
Thinking about this further, one cause is the limited controllability in the "X" direction. While movement of the hip alone can control Y fairly well, X motion in this range requires synchronized motion of both motors. More importantly, through some of this region the leg is nearly straight out, which gives very little control authority for pushing outwards. As an extreme example, consider the following. In this case, only the hip motor moved and the knee was straight. It is clear that near the front of the desired profile, the leg is nearly straight.

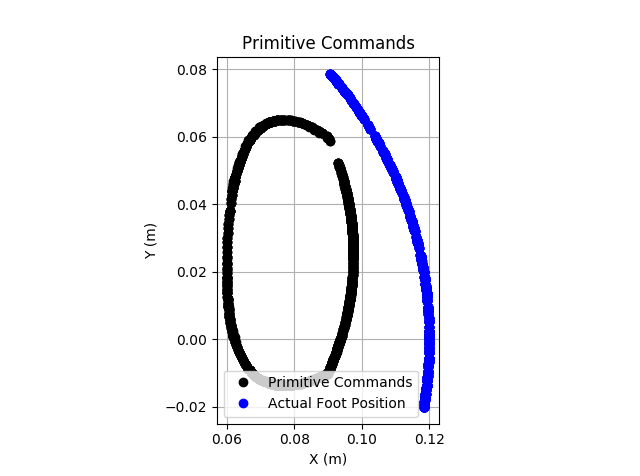
Some of the tracking issues also seemed to be temporal, that they cannot keep up with the speeds. I therefore ran a test with a 3s period to show how the control is working. In this case, the virtual model control actually works decently well. Although the actual shape doesn't match perfectly, it is clearly better than previous attempts.

That is where is stands for now. I believe there are a few things I can do to improve this:

• Stiffen up VMC and current controller to track motion faster
• Generate new motion profiles that provide better conditioning for VMC