Matrices Denavit-Hartenberg (DH)

"Se trata de un procedimieto sistemático para describir la estructura cinemática de una cadena articulada constituida por articulaciones con. un solo grado de libertad."

Las matrices DH son matrices que describen la relacion entre los eslabones de una cadena ciematica y describen la forma del robot de forma numerica, utilizando los angulos y las distancias en los ejes z y x de cada uno de los eslabones para pasar de una junta a la siguiente junta. Estas matrices son importantes ya que de alguna manera codifican la estructura del robot/manipulador y la relacione entre eslabones y juntas. Estas matrices son la clave para poder codificar tanto la cinematica directa como la inversa de cualquier robot. El procedimiento para generar las matrices es relativamente sencillo

1. Se comienza en la primera junta, y se define el sistema de coordenadas en la junta, con el eje z perpendicular a la junta y el eje x paralelo a la misma
2. Se denota la distancia que se debe desplazar verticalemente (eje z) de la primera junta a la siguiente como d1 
3. Se denota la distancia que se debe desplazar horizontalmente de la primera junta a la siguiente como a1 
4. Se denota la rotacion que se debe de hacer en el eje z para coicidir con el marco de referencia de la siguiente junta como theta1
5. Se denota la rotacion que se debe de hacer en el eje z para coicidir con el marco de referencia de la siguiente junta como alfa1
6. Se hace el mismo proceso de pasar de una junta a la siguiente hasta agotarse la juntas.

Con lo que se obtiene una matriz como esta:

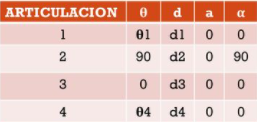
En el caso de nuestro hexapodo con 2 grados de libertad, se tienen solo dos articulaciones. En este caso nuestra matriz DH seria una matriz 4x2. Basandonos en la siguiente representacion para la pata y las siguientes medidas obtenemos:

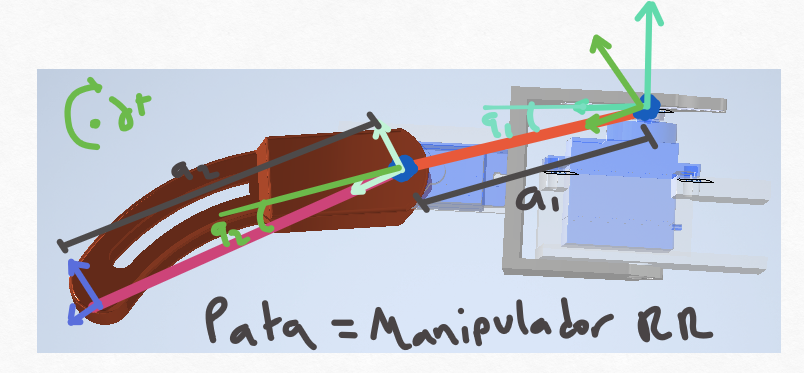
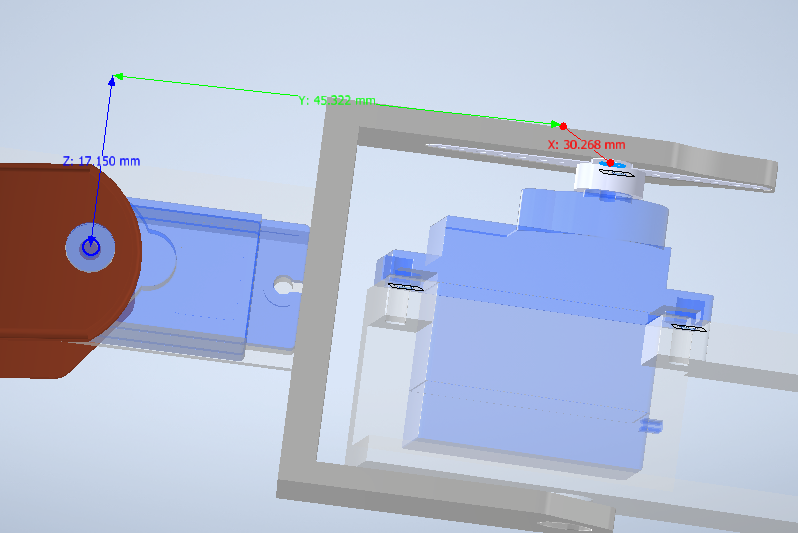
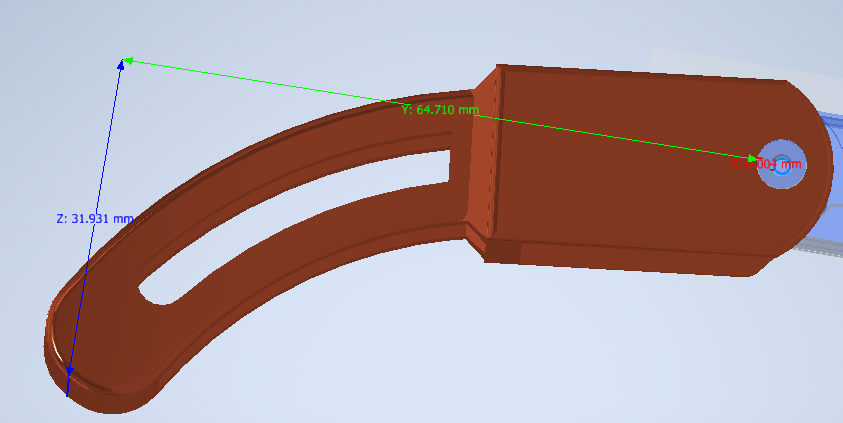
Nuestra tabla DH seria entonces:

	d	a
q1	1.72 cm	4.53cm	90
q2	0	6.47cm	0

Utilizando las siguientes eqcuaiones:

Podemos encontrar nuestra matrix DH como una multiplicacion de A1*A2

Con esto en mente utilizamos el siguiente codigo para encontrar la matriz DH de nuestra pata de dos eslabones

Lo cual nos da que nuestra matriz DH es:

Transformaciones de Base

Las transformaciones de base sirven para ubicar cada pata segun su ubicacion relativa a origen global del sistema. En este caso el origen global del sistema es  centro del hexapod, donde se encuentra el arduino nano. Para este caso y dado que las patas tienen la misma forma, se puede utilizar la misma matriz DH para cada pata.Solo se necesita trasladar cada pata a su ubicacion en el hexapod, y luego rotarla en el eje z para que coincida con como esta orientada.

Procedemos a definir las transformaciones base de cada pierna de la siguiente manera, como simples rotaciones sobre el eje Z y desplazamientos en X y Y:

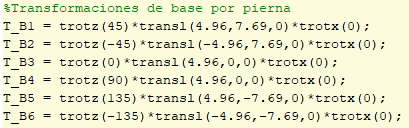
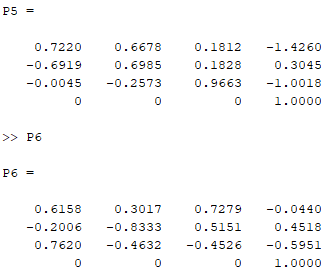
Entonces podemos encontrar que nuestra matriz DH de cada pierna es tan solo la multiplicacion de la matriz DH general x La Transformacion Base. Esto nos da para cada pierna (cuando el angulo q1=0 y q2=0):