Para realizar la transformación de la base de nuestro robot hacia el efector final se utilizarán matrices de transformación. La cinemática directa completa para manipuladores seriales se define como:

Para construir las matrices, se utilizará la convención de Denavit-Hartenberg. Esta nos dice que cada junta está unida por medio de un eslabón y una junta previa. Para cada junta, se tiene una matriz A que describe la traslación y rotación necesaria para ir de la junta N-1 a la junta N. Cada junta en esta convención, tiene asociado únicamente un grado de libertad. En este caso, únicamente se cuenta con 3 juntas revolutas por extremidad, por lo que el vector de configuración q de cada extremidad se definirá como:

En donde todas sus componentes son ángulos en grados. Con esto en consideración, el teorema de Denavit-Hartenberg dice que la matriz de transformación entre {B} y {E} está dada por:

Estas matrices A sirven para definir de igual manera las matrices de transformación de base y herramienta. Entre cada extremidad, la única que varía es la transformación de base, por lo que estas se definirán primero:

donde las funciones Rot y Transl son generan matrices de rotación y translación homogéneas respectivamente en los ejes dados por los subíndices; y n es el número de extremidad entre 1 y 4. El número de extremidades junto con los respectivos marcos de referencia se muestran a continuación.

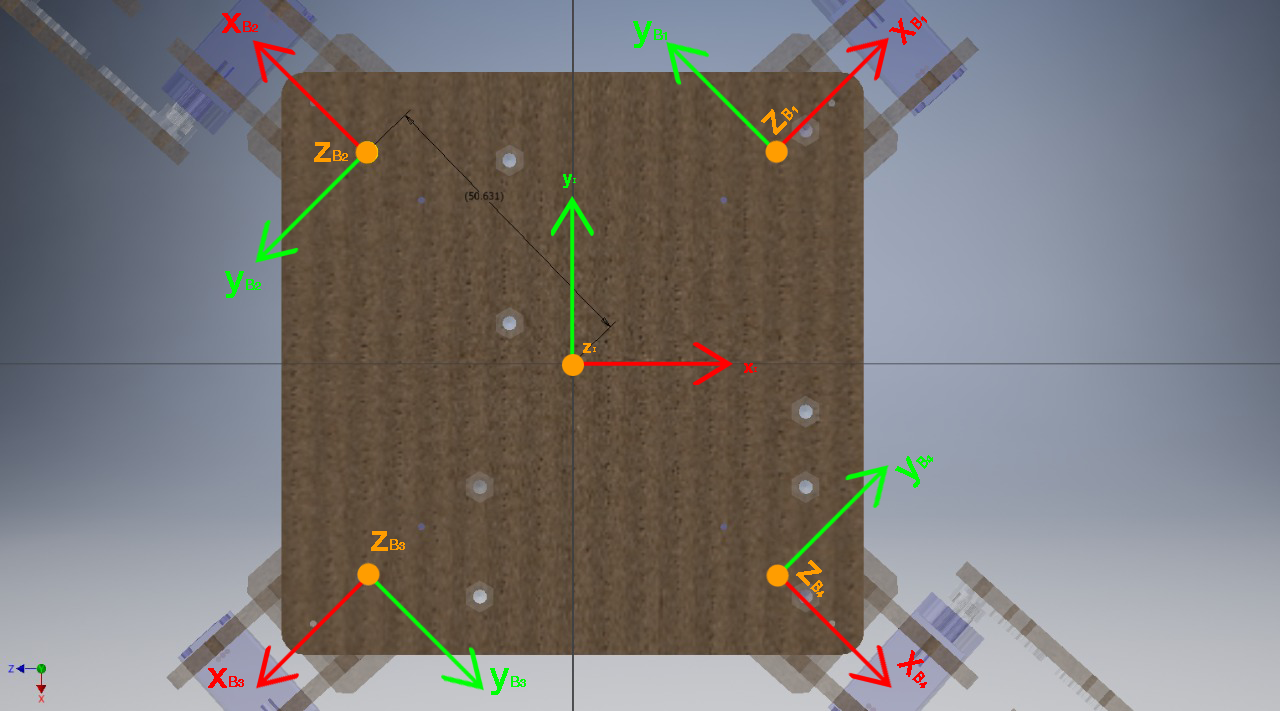
Utilizando las mismas fórmulas y con los marcos de cada junta como se muestran a continuación, se llegan al conjunto de matrices:

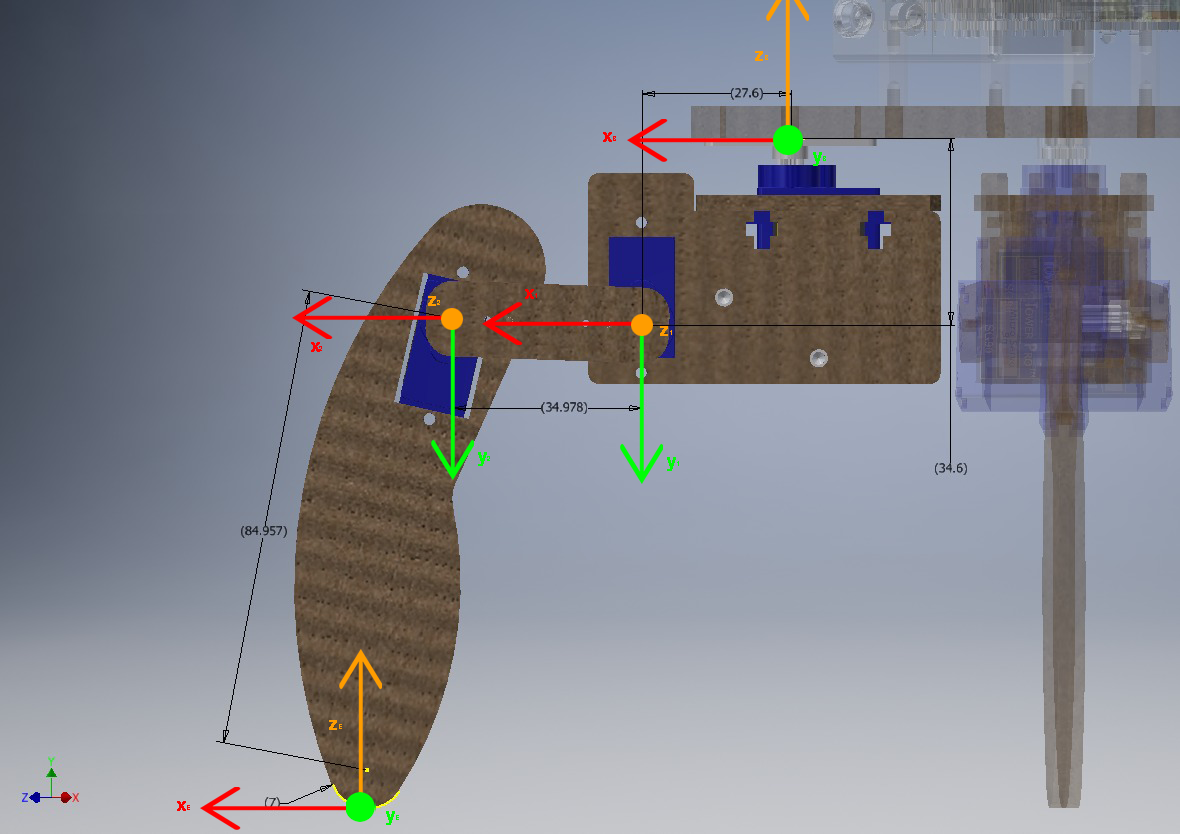
Cabe mencionar que la segunda y tercera junta, a pesar que la unión tiene un desfase en sus ejes Z locales, estos no se toman en consideración en las matrices. Y que, al no tener un efector final externo (como una garra, taladro, ventosa, etc.), no se necesita de una transformación de herramienta (o se puede utilizar una matriz identidad). 

La multiplicación de las 3 matrices A encontradas anteriormente se define una extremidad. Y al todas ser iguales, lo único que cambia entre es la transformación de base. Evaluando numéricamente las matrices con ayuda de Matlab y la Robotics Toolbox de Peter Corke se obtienen la matriz de las extremidades de: