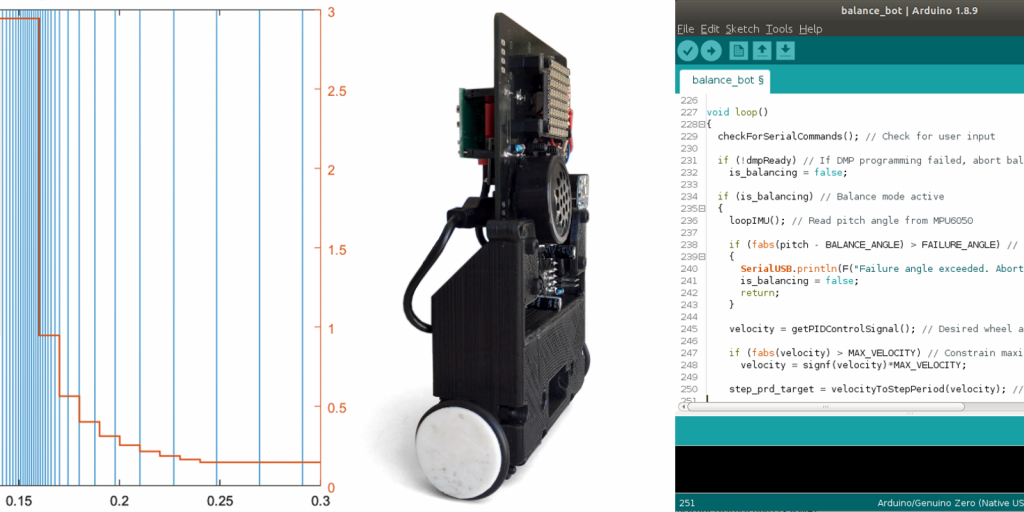
In order to balance our little guy, we’re going to read in data from our inertial measurement unit (IMU), create a PID controller to catch the robot from falling, and write an accurate stepper motor controller from scratch. We’ll also read in commands from serial input, in order to tweak and configure our controller on the fly.
I won’t give code snippets for every section of the program I’ve written, as that will make this post quite messy and detract from providing a concise overview. Instead, you can find my full program on my Github in the balance_bot repository, and refer to any code I mention here but don’t explicitly show. Keep in mind that some of the examples I give are simplified for clear explanation, so be sure to check out my Github if you want to implement something similar. Let’s get cracking!
Measuring angles with an MPU6050
The key piece of information we need to get our robot to balance, is the current pitch angle of the robot, which we’ll read from our MPU6050 IMU. To do this, I adapted some code from Jeff Rowberg’s MPU6050 library (as many do) for Arduino, specifically the MPU6050_DMP6 example. DMP stands for Digital Motion Processor, which is basically some circuitry in the chip which pre-processes the sensor values for us, meaning less work for us in the code.
We take three main things from this example code. Firstly, some global variables which the program needs, namely the MPU6050 object, some flags, buffers, and vectors to store the sensor readings. You’ll find these defined in my code here. Secondly, we need to begin communication with the IMU and initialise the DMP unit, the code for which you’ll find in my setupMPU6050() function.
Thirdly and finally, my loopIMU() function waits for an IMU reading to be available, and then calculates the robot’s pitch angle, storing it in a global variable called “pitch“. These measurements take less than 10ms to be available, meaning I’m able to call this function during each main loop and maintain it at a consistent 100Hz. This consistency is important for reliable control, which we’ll need, unless we want to see this guy on his face.
One last thing. To make the angle reading as reliable as possible, you should run the IMU_Zero example in the MPU6050 library, following its instructions, in order to calibrate your specific chip. The output from this example program is a number of offset values, which you need to add to the setup code in setupMPU6050(), in the following section:
// Accelerometer and gyrometer offsets.
mpu.setXGyroOffset(-1535);
mpu.setYGyroOffset(-255);
mpu.setZGyroOffset(36);
mpu.setXAccelOffset(-2947); mpu.setYAccelOffset(-5297);
mpu.setZAccelOffset(2365);
The values currently there are specific to my chip, and likely will cause inaccuracies with your own, so be sure to calibrate! Now, let’s do something with this angle.
PID control
If we want our little guy to stay upright, we’ll have to command his wheels to turn in such a way that he maintains an angle of about 90 degrees. A common control method used to address this is a PID controller, which we’ll use here. I won’t go into much detail about it, but essentially it uses the error between the desired angle (the setpoint) and measured angle (the observation), the accumulation of that error over time, and the rate of change of that error, in order to send commands to the wheels (the control signal).
This might sound like a mouthful, but a basic implementation doesn’t require much code at all. I implemented it with a handful of global variables and a function, but I’d recommend using a struct (similar to a class in C++), or creating/using a library to keep things cleaner. It can be valuable to write it yourself, or at least see how someone else’s library works, in order to learn how it works, and perhaps to make sure it doesn’t have too much overhead for low-latency applications like this.
The following snippet shows the core parts of my PID controller:
float Kp, Ki, Kd; // PID gain values
float err, err_prev, err_d, err_i; // Error terms for controller
float setpoint; // Desired robot pitch to maintain
... // Set gain values, zero initial errors, suitable setpoint
float getPIDControlSignal()
{
err = setpoint - pitch; // Calculate error term
err_i += err; // Estimate integral of error
err_d = err - err_prev; // Estimate derivative of error
err_prev = err; // Store current error to use in next calc
return Kp*err + Ki*err_i - Kd*err_d; // Return control signal
}
We can see that the control signal calculation returned from getPIDControlSignal() is the sum of three terms, each with its own constant coefficient, Kp, Ki and Kd. These constants are called the gains, and determine what proportion of each type of error we care about in calculating our output. The function is called in our main loop, at a consistent rate of 100Hz.
If our control signal were instead computed at irregular times, it would be more accurate to instead compute the error integral by adding err*dt and the error derivative as (err – err_prev)/dt, where dt is the time elapsed since the previous calculation. Since the time elapsed between calculations is consistent in my program, we can essentially absorb the dt into the constants Ki and Kd, which need to be tuned and tweaked anyway.
You might be wondering what happens in the magical “…” section between the variable declarations and the function, where we claim to set the gains and the setpoint. This step is actually crucial and not to be glossed over, but essentially, we allow the gains and setpoint to be provided via the serial monitor. This means we can test out different values very quickly, avoiding the need to recompile and reupload every time we want to change the numbers. Read on to see how this is done!
Hardware-timed stepper motor controller with acceleration
Well, we’re not going to get much balancing done unless we can use our stepper motors. For this, we’re going to write our own stepper motor controller, so we can learn a thing or two. The foundation of this controller was inspired by the code from YABR project, but written for use on a Cortex-M0+ CPU instead of an ATmega. We’re also going to take it one step further and perform acceleration control using a hardware timer/counter and an additional algorithm.
The Exen Mini microcontroller has an ARM Cortex-M0+ as its processor, and we will make use of its hardware capabilities to generate signals that our stepper driver chip needs to turn our motors. The A4988 stepper driver can control a stepper motor with two input pins: STEP, and DIR. As the name suggests, DIR controls the direction of rotation by simply pulling the pin high or low. STEP, on the other hand, turns the stepper motor output by one “step” for each pulse it receives on the pin, i.e. a high voltage followed by a low voltage.
In this way, we can see that the speed of the stepper output will be determined by how many pulses we send to the A4988’s STEP pin per second. So if we want to control our speed, we’ll need access to something in our program that allows precise timing. Enter the TC!
Setting up a hardware timer/counter on a Cortex-M0+
The Cortex-M0+ has a number of TC (timer/counter) units available to us, which we can configure to periodically trigger an interrupt service routine (just a function) at a rate that we specify. We’ll use TC4 to generate our STEP pulses, and I’ll note that I used the specifics of the timer setup from this forum post. Here’s what the code looks like for setting up TC4, and beware, it’s a little hairy:
// Set up generic clock GCLK4
REG_GCLK_GENDIV = GCLK_GENDIV_DIV(1) | // Divide 48MHz clock source by 1, keep the same
GCLK_GENDIV_ID(4); // Select GCLK4
while (GCLK->STATUS.bit.SYNCBUSY); // Wait for synchronization
REG_GCLK_GENCTRL = GCLK_GENCTRL_IDC | // Set duty cycle to 50/50 HIGH/LOW
GCLK_GENCTRL_GENEN | // Enable GCLK4
GCLK_GENCTRL_SRC_DFLL48M | // Set the 48MHz clock source
GCLK_GENCTRL_ID(4); // Select GCLK4
while (GCLK->STATUS.bit.SYNCBUSY); // Wait for synchronization
// Feed GCLK4 to TC4 and TC5
REG_GCLK_CLKCTRL = GCLK_CLKCTRL_CLKEN | // Enable GCLK4 to TC4 and TC5
GCLK_CLKCTRL_GEN_GCLK4 | // Select GCLK4
GCLK_CLKCTRL_ID_TC4_TC5; // Feed GCLK4 to TC4 and TC5
while (GCLK->STATUS.bit.SYNCBUSY); // Wait for synchronization
// Set up timer TC4 at 46.875 kHz for stepper pulse control
REG_TC4_COUNT16_CC0 = 0; // Set TC4 CC0 register as TOP value in MFRQ
while (TC4->COUNT16.STATUS.bit.SYNCBUSY); // Wait for synchronization
NVIC_SetPriority(TC4_IRQn, 0); // Set the NVIC priority for TC4 to 0 (highest)
NVIC_EnableIRQ(TC4_IRQn); // Connect timer TC4 to NVIC
REG_TC4_INTFLAG |= TC_INTFLAG_OVF; // Clear the interrupt flags
REG_TC4_INTENSET = TC_INTENSET_OVF; // Enable TC4 interrupts
REG_TC4_CTRLA |= TC_CTRLA_PRESCALER_DIV1024 | // Set prescaler to 1024, 48MHz/1024 = 46.875kHz
TC_CTRLA_WAVEGEN_MFRQ | // Put timer TC4 into match frequency (MFRQ) mode
TC_CTRLA_ENABLE; // Enable TC4
while (TC4->COUNT16.STATUS.bit.SYNCBUSY); // Wait for synchronization
This looks nasty, but basically we’re just setting a bunch of register values that TC4 needs to do its job. We first give the timer a 48MHz clock source, enable interrupts, and set the timer prescaler to 1024, which results in the timer running at 48MHz/1024 = 46.875kHz. The upshot of this is we get access to a function called TC4_Handler(), an interrupt service routine, which will be called 46,875 times per second. That’s the kind of precision we need to control our stepper speed!
Writing the stepper controller
So we now have a precisely timed function which we can use to generate a waveform of pulses to send to our A4988 stepper driver. But how do we decide how many pulses to send per second? Well, we have a desired angular velocity given as the output of our PID controller, and we can use this to calculate our pulse rate.
The key to converting between angular velocity and pulse rate is in knowing the number of steps the stepper motor needs to rotate in order to complete a full revolution. The datasheet gives us the angle rotated by the shaft per step, 0.18°, in our case, so we simply divide 360 degrees by that angle in order to acquire the number of steps per revolution. For us, this works out to 2000 steps/rev.
I’ll give an example of the this calculation. Suppose we want to turn the stepper motor at π radians (180°) per second. If we divide this figure by 2π, we get the desired number of revolutions per second, namely 0.5 rev/s in our example. If our motor requires 2000 steps/rev, then multiplying this with our desired 0.5 rev/s gives us a requirement of 1000 steps per second, and this is our pulse rate.
How do we provide 1000 steps, or in other words 1000 pulses per second? Well, we know our interrupt service routine TC4_Handler() will be running at 46.875 kHz, or 46,875 times per second. To achieve the desired angular velocity, we therefore need to space these 1000 pulses evenly throughout the 46,875 function calls. So finally we have our answer, by dividing 46,875 by 1000, giving approximately 47.
So every 47 calls to TC4_Handler(), we want to send out a pulse to the stepper driver’s STEP pin to produce one stepper motor step, in order to rotate at π radians per second. In essence, what we have calculated is the period of our desired pulse waveform. Putting all this together, we get a calculation that looks like the following:
float velocityToStepPeriod(float velocity)
{
if (fabs(velocity) > 0.01)
return round(TICKS_PER_SEC/((velocity/(2*M_PI))*STEPS_PER_REV));
else
return signf(velocity)*ZERO_PRD; // Avoid division by zero
}
Note that TICKS_PER_SEC is our figure 46,875, the number of timer/counter “ticks” per second. We’ve also included an additional check to avoid divison by zero when the velocity is zero, and we instead return a large value ZERO_PRD which is high enough to consititute no movement at the stepper output. The output of this conversion, such as the “47” from our previous example, is what I’ll refer to from here on as the stepper pulse period, or stepper period.
So at this point, our main loop looks a little something like this:
loopIMU(); // Read robot pitch angle from MPU6050 IMU velocity = getPIDControlSignal(); // Desired wheel angular velocity step_prd_target = velocityToStepPeriod(velocity); // Get stepper period
We store our target stepper pulse period in a global variable called step_prd_target, which we’ll use (in some form) in our interrupt service routine to generate the appropriate pulse rates. And now for the long-awaited TC4_Handler()!
/* Interrupt Service Routine (ISR) for timer TC4 */
void TC4_Handler()
{
// Check for overflow
if (TC4->COUNT16.INTFLAG.bit.OVF && TC4->COUNT16.INTENSET.bit.OVF)
{
prd_counter++; // Increment pulse period counter
// Check if period has expired
if (prd_counter >= step_prd_cur)
{
prd_counter = 0; // Reset counter to prepare for next pulse
}
else if (prd_counter == 1) // Beginning of period
{
setStepperDirections(step_prd_cur_raw); // Set stepper directions
// Set lines high to pulse
REG_PORT_OUT1 |= PORT_PB09; // STEP_R high
REG_PORT_OUT0 |= PORT_PA05; // STEP_L high
}
else if (prd_counter == 2)
{
// Set lines low to finish pulse
REG_PORT_OUT1 &= ~PORT_PB09; // STEP_R low
REG_PORT_OUT0 &= ~PORT_PA05; // STEP_L low
}
REG_TC4_INTFLAG = TC_INTFLAG_OVF; // Clear the OVF interrupt flag
}
}
In summary, we’re using a variable prd_counter to keep track of how many timer ticks have elapsed, generating our pulse at the start of the period (by setting the port registers directly), and triggering the end of the period by comparing prd_counter with our period step_prd_cur. Note that we also change the direction of the steppers via the function setStepperDirections(), which sets the stepper driver’s DIR pin high or low.
But wait, you said we’re using a global variable step_prd_target! Well, actually use it to set variables called step_prd_cur and step_prd_cur_raw, which are the current stepper period, and a raw version of the period which encodes a direction as well. Why don’t we directly give it the target target period? The answer is that we need to accelerate towards our desired velocity.
Adding acceleration to our controller
You might look at the previous code snippets where we developed the stepper control algorithm and think, that’s all we need right? We’re taking speed commands, calculating periods, and turning them into regular pulses to the stepper driver. Well, there are a couple of things about stepper motors that means our previous code will fail in some common circumstances, if we don’t introduce acceleration.
If you look at a stepper motor datasheet, you’ll see a term called the “maximum starting frequency”. As the name suggests, the motor has a maximum frequency up to which the stepper can be started from rest. As the frequency corresponds to the speed, the motor essentially has a cap on the speed it can be started at. If we try to start it at a speed above the maximum, the most we’ll get out of it is some pitiful whining noises.
What’s the solution? We need to accelerate towards desired speeds, rather than directly commanding them. We’ll do this by keeping track of a couple of variables, step_prd_target and step_prd_cur, which correspond to the desired and current speeds, respectively. At a consistent rate, we will move the current speed closer to the desired speed, in increments. In this way, we avoid ever exceeding the maximum starting frequency, but we also take care to accelerate fast enough so our stepper controller responds quickly to commands.
Testing the acceleration algorithm in Octave
When designing non-trivial algorithms such as this, it can be helpful to visualise the results to make sure it’s performing as expected, rather than shoving them into your microcontroller and hoping they work! I implemented the acceleration algorithm in Octave (open-source Matlab) to do exactly this.
So, how will we increment our current speed towards the desired speed? The initial temptation is to perform a simple a linear interpolation between the values. But remember, we’re working in the domain of stepper pulse periods, and the relationship between our angular velocity and stepper period is not linear. This is demonstrated in Figure 1 below:
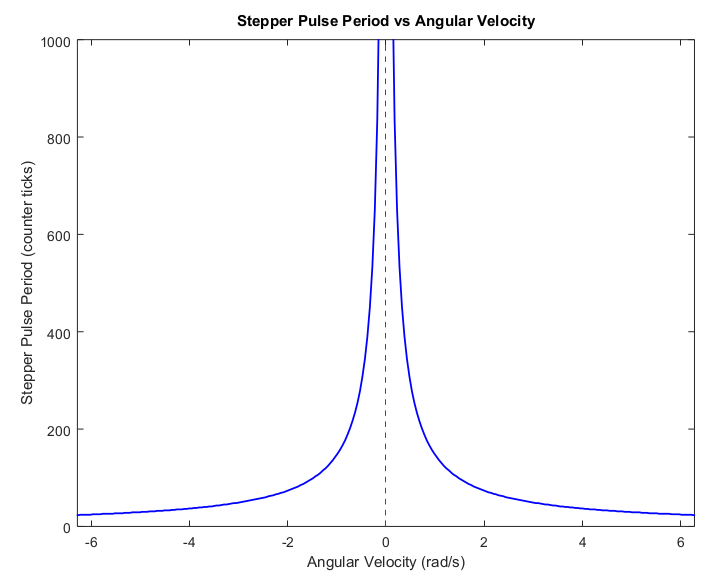
Figure 1: Stepper pulse period vs angular velocity, showing the nonlinear relationship between the two variables.
From this relationship, we can see that linearly interpolating between the different periods will result in non-constant acceleration – which isn’t ideal. We could instead store our commands as velocities and interpolate them before converting them to stepper periods, but then we’d need to do a velocity-to-period conversion every time we run our main stepper loop TC4_Handler(), which runs thousands times per second, so it would be very inefficient to include this calculation in each loop.
In order to be efficient, let’s perform a nonlinear interpolation between stepper periods, at a consistent rate, such that we achieve a constant acceleration. The following calculation can do exactly that for us, interpolating from the current period p_cur to the desired period p_des.
const int F_inc = 50; // Frequency (PPS) increment per acceleration interpolation step
const float BETA = (float)F_inc/TICKS_PER_SEC; // Constant for acc calc
int accelerate(int p_cur, int p_des)
{
return round( 1.0/(1/p_cur - sign(p_des - p_cur)*BETA) );
}
What’s going on here? I won’t do a derivation, but essentially we invert the current period to obtain a frequency, add or subtract a constant frequency increment from it (depending on whether the desired period is smaller or larger), then invert it again to obtain an interpolated period. This works because the velocity is proportional to the frequency, so linear frequency interpolation results in linear velocity interpolation.
I implemented the algorithm in Octave, and tested it with a couple of velocity command profiles as inputs. The first of these was a profile featuring a high-velocity command in the middle, the result of which is shown in Figure 2 below:
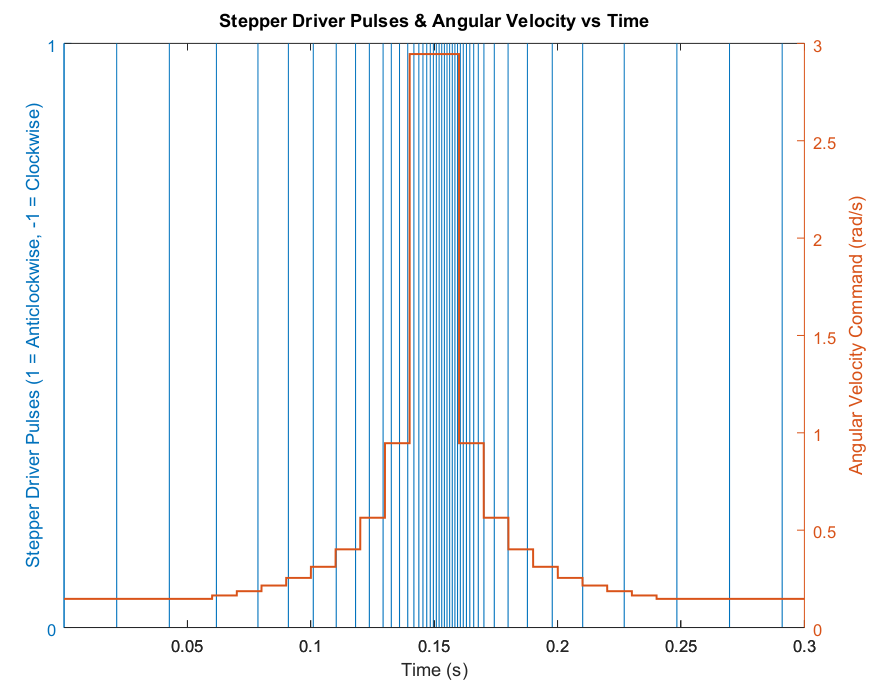
Figure 2. Stepper driver pulses in response to an angular velocity command profile.
We can see the velocity command profile in red (with axis units on the right), and the resulting stepper driver pulses in blue (with axis units on the left). We observe smooth transitions between different speeds, shown by gradual changes in the stepper periods (the distance between blue lines), rather than rapid changes. Note the slight delay in achieving the command velocity at the center of the graph, as it takes a little bit of time to accelerate.
I also tested the algorithm with a sinusoidal velocity profile, shown in Figure 3 below:
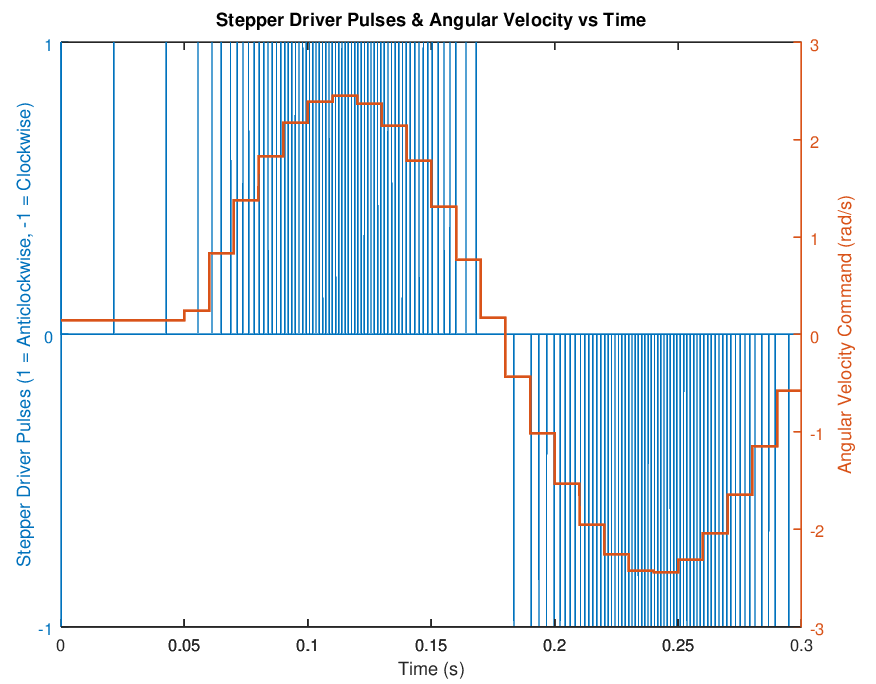
Figure 3. Stepper driver pulses in response to a sinusoidal angular velocity command profile.
Again, we see a continuous transition between stepper periods as a result of the acceleration. Here, we represent the motor output direction by a negative stepper pulse for the purpose of visualisation, whereas in reality, we instead set the DIR pin high or low on the stepper driver chip to achieve this.
Coding up the acceleration
So what does this look like as code? First of all, we set up another timer/counter, this time TC5. You can see the full TC setup code here, for both TC4 and TC5. This time, we make proper use of the counter, and set it to overflow at a rate of 1000Hz, by setting TC5’s CC0 register to the appropriate value. By checking for this overflow inside the interrupt service routine TC5_Handler(), we can perform our acceleration interpolation at a rate of 1000Hz. This should be plenty enough speed for smooth interpolation, as we verified in Octave earlier.
Alright, let’s use TC5_Handler() to perform our nonlinear interpolation of the stepper periods. Here’s what the interrupt service routine looks like:
/* Interrupt Service Routine (ISR) for timer TC5 */
void TC5_Handler()
{
// Perform acceleration interpolation upon counter overflow
if (TC5->COUNT16.INTFLAG.bit.OVF && TC5->COUNT16.INTENSET.bit.OVF)
{
// Check which side of period-velocity profile we need to get to
if (sign(step_prd_target) == sign(step_prd_cur_raw)) // SAME side of profile
{
// Perform acceleration interpolation to change speed
step_prd_cur_raw = accelerate(step_prd_cur_raw, step_prd_target);
step_prd_cur = abs(step_prd_cur_raw);
}
else // Need to move to OPPOSITE side of period-velocity profile
{
if (abs(step_prd_cur_raw) < ZERO_PRD) // If we haven't slowed to zero yet
{
// Slow the stepper to zero
step_prd_cur_raw = accelerate(step_prd_cur_raw, sign(step_prd_cur_raw)*SWAP_PRD);
step_prd_cur = abs(step_prd_cur_raw);
}
else // Slowed to zero already
{
// Swap side of period-velocity profile and dip below the zero threshold
step_prd_cur_raw = -sign(step_prd_cur_raw)*(ZERO_PRD - 1);
}
}
REG_TC5_INTFLAG = TC_INTFLAG_OVF; // Clear the OVF interrupt flag
}
}
So what’s all this? This is where step_prd_cur and step_prd_cur_raw come into play. These are actually quite simple; step_prd_cur_raw is the period resulting from interpolation between the current stepper period and the target stepper period, and it can be negative, encoding its direction. And step_prd_cur is simply the absolute value of its raw counterpart, for easy comparison with the period counter in our stepper control loop.
But why so many conditionals here? If you look back to Figure 1, you can see that as we approach zero velocity, the stepper period approaches infinity, on both sides. Clearly, we can’t store infinite period values, so at some point we need to put a limit on how large a period we can define, and we call this ZERO_PRD, which has a value of 10,000 in my code. The point is, if we want to change the motor’s direction, we need to increase the period up past some value ZERO_PRD, switch the polarity of the raw stepper period step_prd_cur_raw to indicate a change of direction, then start decreasing the period down from ZERO_PRD again.
If the desired velocity has the same polarity as the current velocity, then all is well and we simply interpolate between them. However, if we want to change direction, we first interpolate towards a larger period SWAP_PRD, which is defined to be larger than ZERO_PRD, and upon reaching it, we switch sides of the profile and can return to normal interpolation again.
This was a bit of work. But in the end, we’ve made a pretty robust stepper controller, with acceleration! We’ll see it in action soon, but first, we need a way to tell our robot what to do.
Reading serial input to receive commands
In order to start and stop our robot, and configure parameters such as PID gains and setpoints on the fly, it’ll be convenient if we can read in values serial commands. We’ll do this in the typical Arduino style and enter commands using the serial monitor, except with the Exen Mini we need to use SerialUSB rather than Serial. Later, we’ll use the same USB serial connection to send commands from the on-board Raspberry Pi Zero.
The checkForSerialCommands() function incorporates all of this functionality, responding to single characters sent in the monitor, such as “s” to start balancing, and “x” to stop balancing. Upon starting, the user is prompted to enter comma separated PID gain values, and then the setpoint value. At this point, the robot will begin trying to balance.
Testing it all on the balance bot
We’ve come all this way, and finally we’re ready to try to balance our little guy! We can read values from our IMU, use it in our PID controller to calculate a velocity command, and then produce that velocity with our stepper motors. Also, we can tell the robot when to begin, and what parameters to use. Perfect!
I spent a while making sure the stepper motor directions were set correctly, adding some extra conditions to the code, and slowly homing in on some good PID gain values. After a little while of testing the robot with the leads connected, I decided to secure the battery in place and take him for a spin, hands free! Once I found the right setpoint, this is how it went:
I think it’s safe to say this was a success! We can see a bit of rocking back and forth in place, which I think can mainly be attributed to the bit of backlash that the stepper motors have.
Thanks a lot for reading, and I hope you got something out of this! Not sure if we'll get around to implementing the forks/face or camera, but who knows.
 Ben Steer
Ben Steer
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.