Goertzel's Algorithm
Here is the core code that works as expected:
// Generate samples
signal=0.0;
for (i=0;i<N;i++) {
// samples[i]=20*((1-0.19)*exp(-i/75.0)+0.19*exp(-i/675.0));
signal=1.0*(i%125==0?1.0-signal:signal);
// signal=sin(2*M_PI*(i%125)/125); // 1kHz
samples[i]=signal;
// Window the data
// data[i]=samples[i]*(0.5-0.35*cos(2*M_PI*i/N)); // Hanning Window
// amplitudeFactor=2.0;
// powerFactor=1.63;
data[i]=samples[i]*(0.54-0.46*cos(2*M_PI*i/N)); // Hamming Window
amplitudeFactor=1.85;
powerFactor=1.59;
}
// Scan frequencies
for (freq=fmin;freq<=fmax;freq+=1) {
w=M_PI*2*freq/SampleFreq;
c=2*cos(w);
s0=0.0;
s1=0.0;
s2=0.0;
for (i=0;i<N;i++) {
// Goertzel
s0=data[i]+c*s1-s2;
s2=s1;
s1=s0;
}
amplitude=amplitudeFactor*sqrt(s2*s2+s1*s1-c*s1*s2)/N;
...
}
The need for windowing
Here is Goertzel's algorithm without windowing:
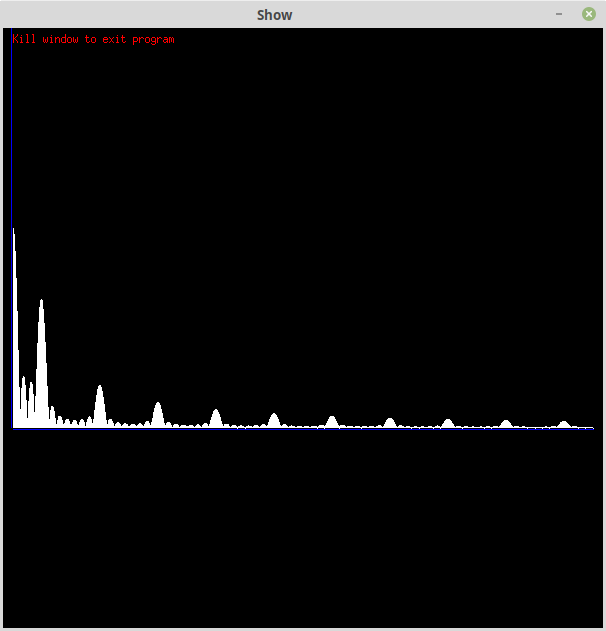
While the peaks are correct what is that background noise? They call it spectral leakage. Basically Goertzel's algorithm see an impulse/sudden start-up/stop, not a continuous 1v/0v square wave. The purpose of windowing is the get rid of the startup noise.
Here is the Hanning window:
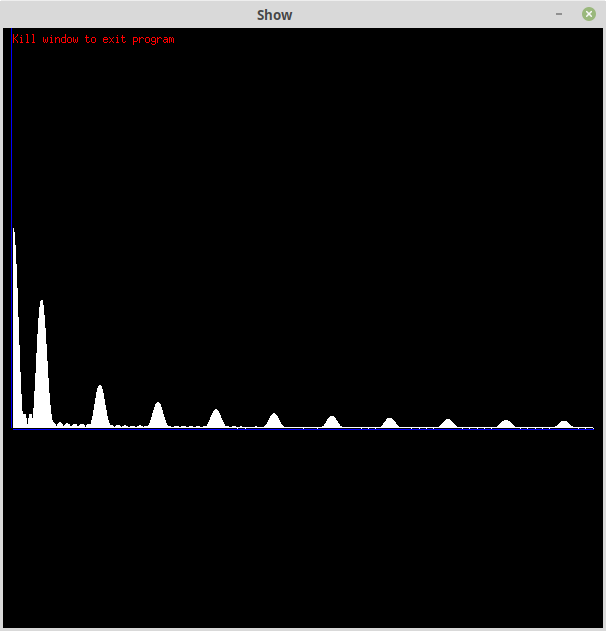
A big improvement but not perfect. Although not the best window to suppress impulse noise, it is the easiest to adjust to preserve the fourier transform magnitudes.
What? Basically the default Hanning window (0.5-0.25*cos(2*M_PI*i/N)) reduces the area of the input signal by 50% resulting in a 50% reduction in the fourier transform magnitude. It is easy to see that multiplying by 2 will fix this problem.
You could work out the adjustment factors for the other windows but not by inspection.
Update
Finally found a reference for this (thanks to Peter Schaldenbrand of Siemens):
https://community.sw.siemens.com/s/article/window-correction-factors
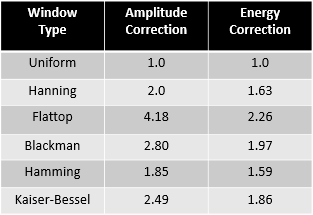
Here it says you can correct the amplitude or the energy (i.e. power) but not both at the same time.
Here is the Hamming window:
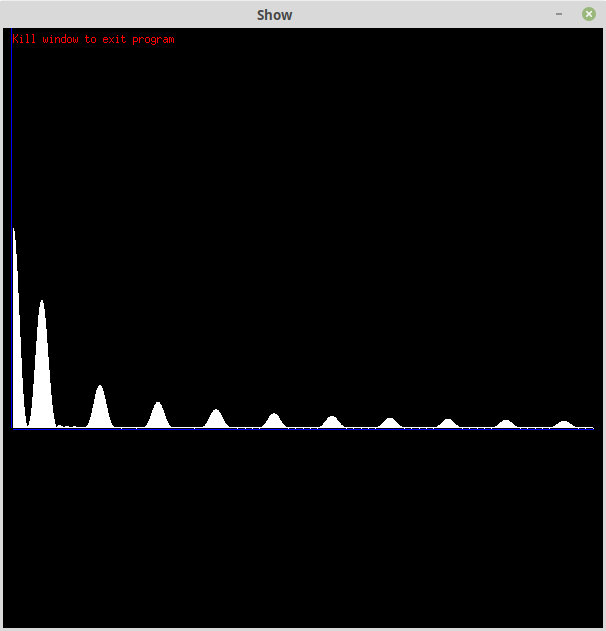
The other correction factors don't match my window functions.
The K Term Problem
k/N=Fc/Fs
where:
Fc = Test (centre) Frequency
Fs = Sample Frequency
N = Number of samples
The problem is that many mathematical texts say that k must be an integer.
In practice this does not appear to be necessary. I use double Fc/Fs rather the integer k/N in my code.
Finally the Power Normalisation problem
It is surprising that so few program codes I have looked did not normalise the power/magnitude (i.e. divide by N^2):
power=(s2*s2+s1*s1-c*s1*s2)/N/N; or amplitude=sqrt(s2*s2+s1*s1-c*s1*s2)/N;
AlanX
 agp.cooper
agp.cooper
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.