Goertzel's Algorithm

Here is the core code that works as expected:

  // Generate samples
  signal=0.0;
  for (i=0;i<N;i++) {
    // samples[i]=20*((1-0.19)*exp(-i/75.0)+0.19*exp(-i/675.0));
    signal=1.0*(i%125==0?1.0-signal:signal);
    // signal=sin(2*M_PI*(i%125)/125); // 1kHz
    samples[i]=signal;
    // Window the data
    // data[i]=samples[i]*(0.5-0.35*cos(2*M_PI*i/N));  // Hanning Window
    // amplitudeFactor=2.0;
    // powerFactor=1.63;
    data[i]=samples[i]*(0.54-0.46*cos(2*M_PI*i/N)); // Hamming Window
    amplitudeFactor=1.85;
    powerFactor=1.59;
  }

  // Scan frequencies
  for (freq=fmin;freq<=fmax;freq+=1) {
    w=M_PI*2*freq/SampleFreq;
    c=2*cos(w);
    s0=0.0;
    s1=0.0;
    s2=0.0;
    for (i=0;i<N;i++) {
      // Goertzel
      s0=data[i]+c*s1-s2;
      s2=s1;
      s1=s0;
    }
    amplitude=amplitudeFactor*sqrt(s2*s2+s1*s1-c*s1*s2)/N;
    ...
}

The need for windowing

Here is Goertzel's algorithm without windowing:

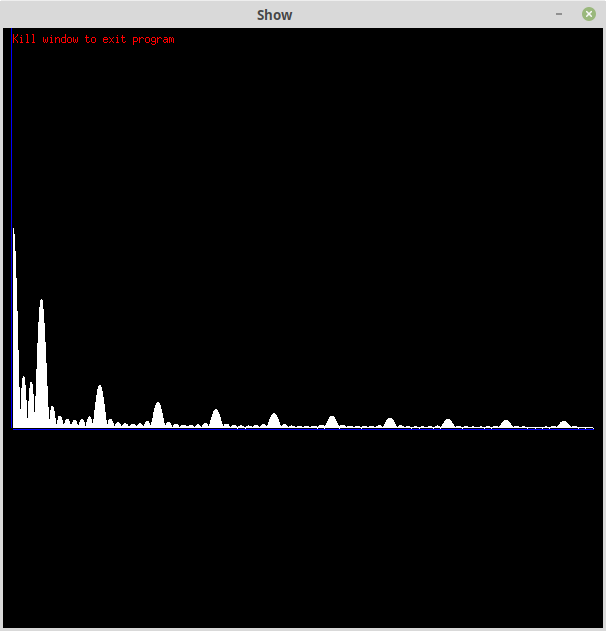
While the peaks are correct what is that background noise? They call it spectral leakage. Basically Goertzel's algorithm see an impulse/sudden start-up/stop, not a continuous 1v/0v square wave. The purpose of windowing is the get rid of the startup noise.

Here is the Hanning window:

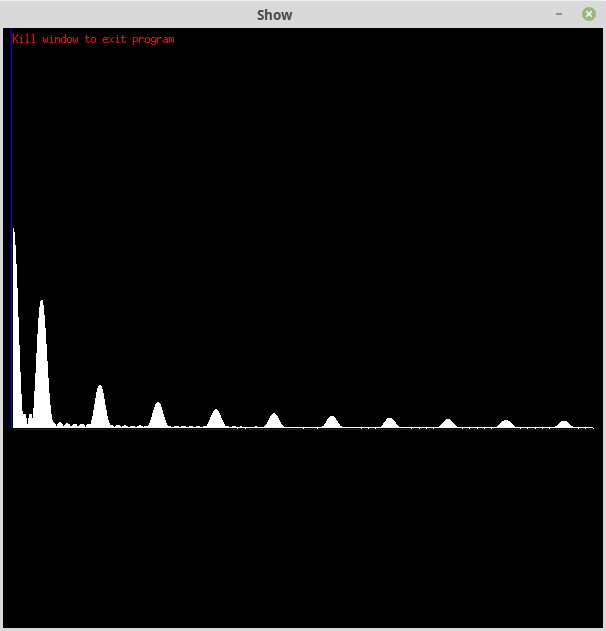
A big improvement but not perfect. Although not the best window to suppress impulse noise, it is the easiest to adjust to preserve the fourier transform magnitudes.

What? Basically the default Hanning window (0.5-0.25*cos(2*M_PI*i/N)) reduces the area of the input signal by 50% resulting in a 50% reduction in the fourier transform magnitude. It is easy to see that multiplying by 2 will fix this problem.

You could work out the adjustment factors for the other windows but not by inspection.

Update

Finally found a reference for this (thanks to Peter Schaldenbrand of Siemens):

https://community.sw.siemens.com/s/article/window-correction-factors

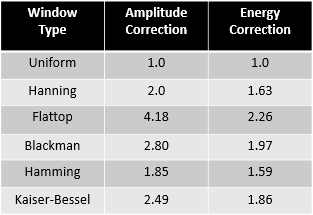
Here it says you can correct the amplitude or the energy (i.e. power) but not both at the same time.

Here is the Hamming window:

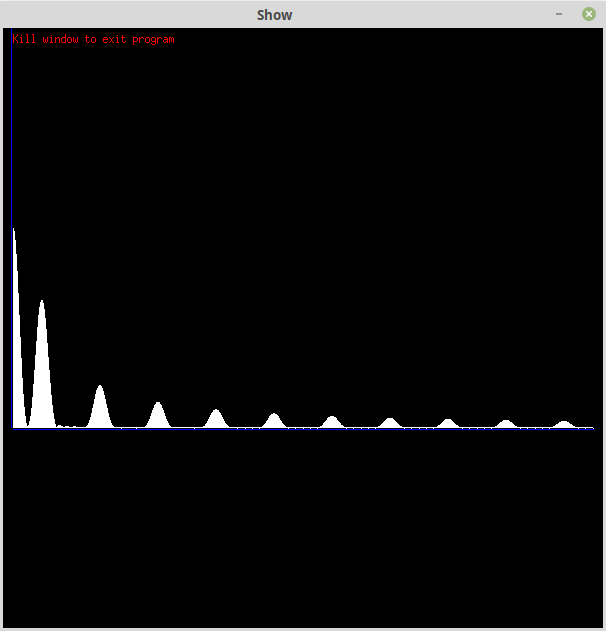
The other correction factors don't match my window functions.

The K Term Problem

  k/N=Fc/Fs

where:

  Fc  = Test (centre) Frequency

  Fs = Sample Frequency

  N = Number of samples

The problem is that many mathematical texts say that k must be an integer.

In practice this does not appear to be necessary. I use double Fc/Fs rather the integer k/N in my code.

Finally the Power Normalisation problem

It is surprising that so few program codes I have looked did not normalise the power/magnitude (i.e. divide by N^2):

power=(s2*s2+s1*s1-c*s1*s2)/N/N;
or
amplitude=sqrt(s2*s2+s1*s1-c*s1*s2)/N;

AlanX