The mathematical descriptor known as Shape Context uses log-polar histograms to encode relative shape information. This can be used to extract alphabet shapes from an image efficiently. The implemented algorithm is as below.
- Log-polar histogram bins are used to compute & compare shape contexts using Pearson’s chi-squared test [12]
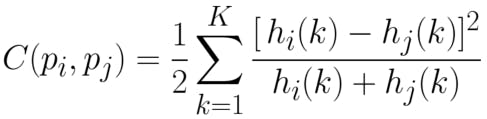
- It captures the angle and distance to randomly sampled (n-1) points of a shape, from the reference point
- To identify an alphabet, find the pointwise correspondences between edges of an alphabet shape and stored base image alphabets. [12]
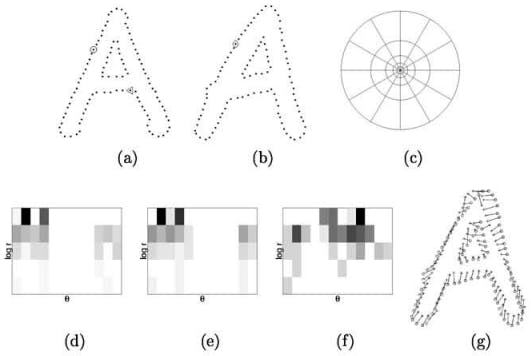
- To identify an alphabet or numeral, find character contours in an image. Filter out the contours based on size and shape to keep the relevant ones.
- Compare contours with each shape inside the base image. The base image contains all the potential characters, both alphabets, and numerals.
- Find the character with the lowest histogram match score
- Do the above for all character contours, to extract the whole text.
# This code builds the shape context descriptor, which is the core of our alphanumeral comparison
# https://github.com/AdroitAnandAI/Multilingual-Text-Inversion-Detection-of-Scanned-Images
# points represents the edge shape
t_points = len(points)
# getting euclidian distance
r_array = cdist(points, points)
# for rotation invariant feature
am = r_array.argmax()
max_points = [am / t_points, am % t_points]
# normalizing
r_array_n = r_array / r_array.mean()
# create log space
r_bin_edges = np.logspace(np.log10(self.r_inner), np.log10(self.r_outer), self.nbins_r)
r_array_q = np.zeros((t_points, t_points), dtype=int)
for m in xrange(self.nbins_r):
r_array_q += (r_array_n < r_bin_edges[m])
fz = r_array_q > 0
# getting angles in radians
theta_array = cdist(points, points, lambda u, v: math.atan2((v[1] - u[1]), (v[0] - u[0])))
norm_angle = theta_array[max_points[0], max_points[1]]
# making angles matrix rotation invariant
theta_array = (theta_array - norm_angle * (np.ones((t_points, t_points)) - np.identity(t_points)))
# removing all very small values because of float operation
theta_array[np.abs(theta_array) < 1e-7] = 0
# 2Pi shifted because we need angels in [0,2Pi]
theta_array_2 = theta_array + 2 * math.pi * (theta_array < 0)
# Simple Quantization
theta_array_q = (1 + np.floor(theta_array_2 / (2 * math.pi / self.nbins_theta))).astype(int)
# building point descriptor based on angle and distance
nbins = self.nbins_theta * self.nbins_r
descriptor = np.zeros((t_points, nbins))
for i in xrange(t_points):
sn = np.zeros((self.nbins_r, self.nbins_theta))
for j in xrange(t_points):
if (fz[i, j]):
sn[r_array_q[i, j] - 1, theta_array_q[i, j] - 1] += 1
descriptor[i] = sn.reshape(nbins) Anand Uthaman
Anand Uthaman
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.