First, I have analyzed the computation of Graph SLAM step by step and then implemented the algorithm efficiently.
Assume a robot in the 2D world, tries to move 10 units to the right from x to x'. Due to motion uncertainty, x' = x + 10 may not hold, but it will be a Gaussian centered around x + 10. The Gaussian should peak when x’ approaches x + 10
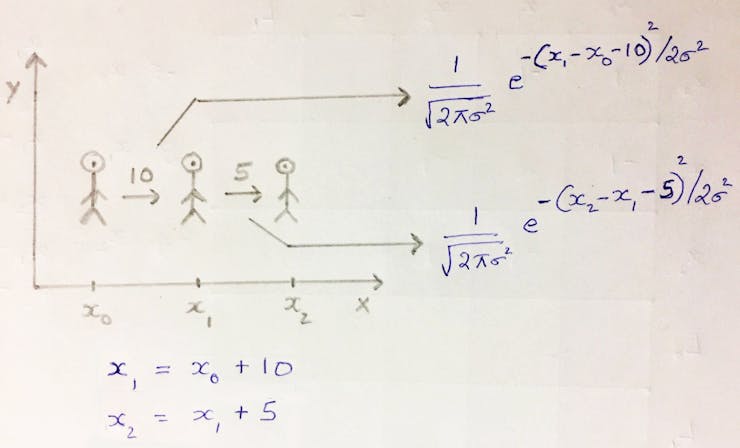
If x1 is away from x0 by 10 units, the Kalman Filter models the uncertainty using the Gaussian with (x1 – x0 – 10). Hence, there is still a probability associated with locations < 10 and > 10.
There is another similar Gaussian at x2 with a higher spread. The total probability of the entire route is the product of the two Gaussians. We can drop the constants, as we just need to maximize the likelihood of the position x1, given x0. Thus the product of Gaussian becomes the sum of exponent terms, i.e. the constraint has only x’s and sigma.
Graph SLAM models the constraints as System of Linear Equations (SLEs), with a Ω matrix containing the coefficients of the variables and a ξ vector that contains the limiting value of the constraints. Every time an observation is made between 2 poses, a 'local addition' is done on the 4 matrix elements (as the product of gaussian becomes the sum of exponents).
Let's say, the robot moves from x0 to x1 to x2 which are 5 and -4 units apart.
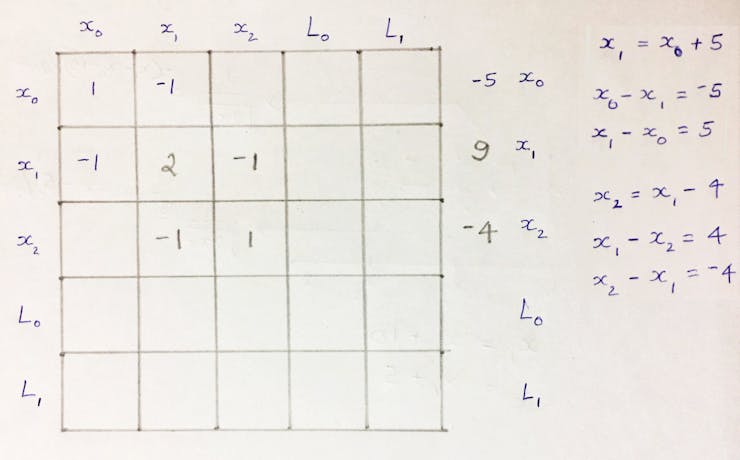
The coefficient of x’s and RHS values are added to corresponding cells. Consider the landmark L0 is at a distance of 9 units from x1.
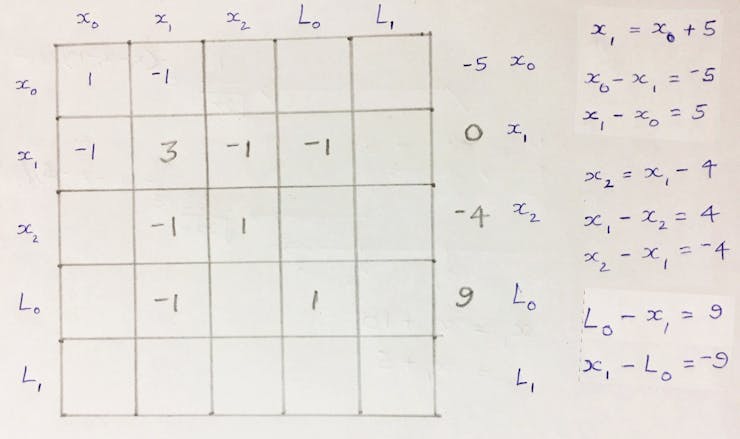
Once the Ω matrix and ξ vector is filled in, as shown above, compute the equation below to get the best estimates of all the robot locations:
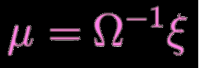
 Anand Uthaman
Anand Uthaman
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.