The signal past the 0.1uF DC blocking capacitor is not very strong, so we need to amplify it. Normally, I would design something with op-amps -- but that would likely mean some form of dual-rail power supply, and parts that cost more than 30 cents -- but this is a *science fiction* contest, and a future where we can afford such luxuries sounds more like high fantasy to me.
So instead, we'll use hex inverters. I like the CD4096, and keep plenty around. They have 6 inverters per chip, which translates to 6 inverting amplifiers, excellent value for money! To make that happen, we just put a 100k resistor between the input and output of an inverter stage, creating a feedback loop. In this design, I use two stages this way.
For details on how this works, you can read more here: https://wiki.analog.com/university/courses/electronics/electronics-lab-20
Overall, this is not only economical, but the resulting amplifier has reasonable bandwidth!
After two stages of amplification, the resulting signal has a maximum amplitude of around 5v and a slight DC bias. We remove that bias with another 0.1uF capacitor, and pass it though a 1k resistor before entering the buffer stage.
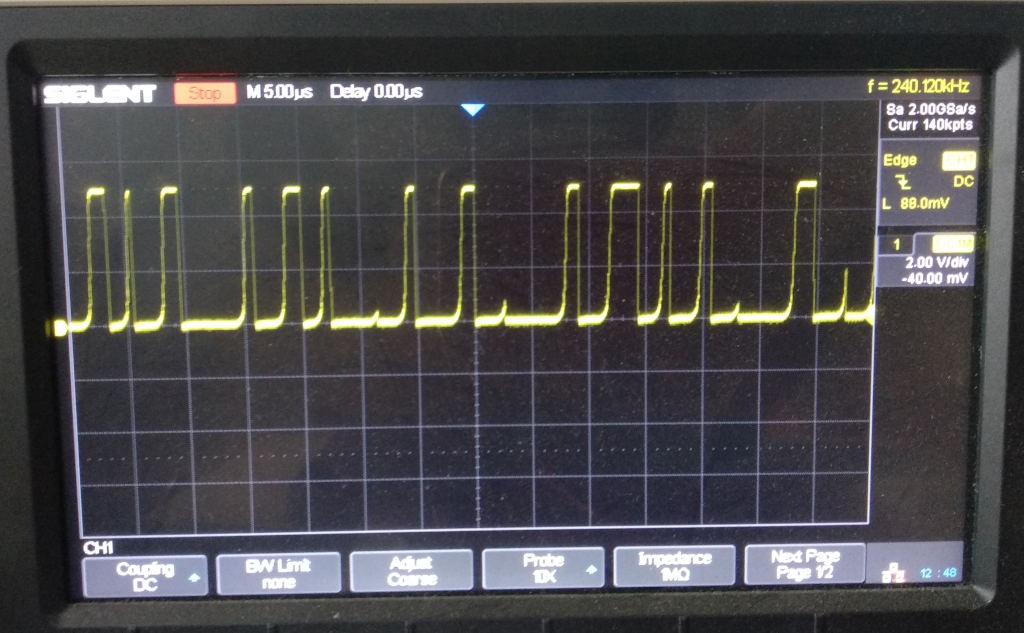
The buffer stage consists of another hex inverter that shares ground with the rest of the circuit so far, but has a regulated 5V supply. This is to ensure that the signal never has a voltage that the microcontroller cannot deal with. We pass it through 2 stages of the hex inverter (no feedback resistors). This both provides a safety margin for our microcontroller (I only had the one unit left), and shortens the rise and fall times for our signal, making it a fairly clean square wave.
With that, we've converted quantum tunneling events to a signal that can be easily processed by a microcontroller! Below is an image of how that looks, any apparent pattern is an artifact of the small sample size:
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.