Once again, the writing for this log is taken directly from an engineering analysis I wrote. This post goes over the equations and simulation results of the hydrophone array. I’ll likely add further simulation results later on.

*from engineering analysis*

The MATLAB simulation will model the fundamental aspects of the hydrophone array solution. This simulation needs to model the acoustic propagation, analog signal conditioning, signal discretization, and the microprocessor algorithm. Using this model, the true target location can be compared to the decoded location, allowing for an analysis of system accuracy, noise tolerance, and computation time. Furthermore, this simulation will provide a clear path for firmware development and finalizes the technical feasibility of the design.

When in water, sound waves travel at a variable speed described by equation (2.1) [3]. This equation depends on the water temperature in Celsius, T, water salinity in parts per thousand, S, and the depth below the surface in meters, D.

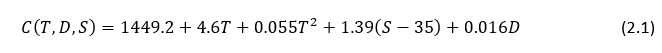
Although the speed of sound is variable, it would help simplify both hardware and firmware design if it could be assumed constant. To gauge the effect of this assumption, equation (2.1) was tested over the range of feasible inputs. When temperature is varied from 0 to 30’C, depth 0 to 50m, and salinity 0 to 35 ppm. The resulting maximum and minimum speeds are 1647.6 meters per second, and 1400.6 meters per second using equation (2.1). Assuming the transducers are separated by 30 millimeters, which is the case for AUVIC’s hydrophone enclosure, the largest propagation delay would result when the target is 90 degrees, or perpendicular, to the AUV’s direction of travel. In this case the time difference of arrivals between the two signals would be at maximum 7.1 microseconds, and at minimum 6.1 microseconds shown in equation (2.2) and (2.3); where, d, is the distance between hydrophones, and, C, is the speed of sound.

Assuming the ADC samples the signal at 100 thousand samples per second (KSPS), this variability will marginally affect the overall accuracy of the system. Furthermore, regardless of the overall accuracy measurements, the algorithm will naturally approach the true location based on the AUV’s movement. For example, assume that every decoded trajectory has an error of 25 percent. After each course adjustment, the AUV comes closer to the target, hence the overall accuracy becomes less and less of a concern. Eventually the AUV will be close enough to the target for the AUV’s optics to take over. For these reasons, the speed of sound in water will be treated as a constant of 1500 meters per second for all subsequent analyses.

Next consider the phase difference of the received signals. The formula to convert this phase shift to the angle of arrival is presented in equation (2.4). This formula is derived from illustration in Figure 1; where, theta, is the direction to the target or angle of arrival, delta t, is the time difference of arrival between the two received signals, and, C, is the speed of sound on water.

Next consider an acoustic wave traveling on a 2D plane as described by equation (2.5) [4]. This formula relates the amplitude of a signal over position and time, where A, is the sending end amplitude, a, is the attenuation constant, f, is the frequency, t, is the time, lambda, is the wavelength, r, is the distance from the emitter to the receiver, and, phi, is the initial phase shift of the signal. For the purposes of this report the equation was modified to incorporate the cartesian coordinate system by making the substitution r=sqrt(x^2+y^2). The modified equation is shown in equation (2.6).

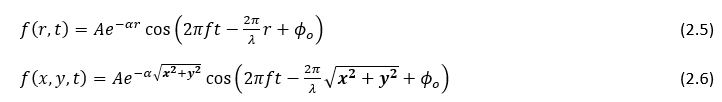
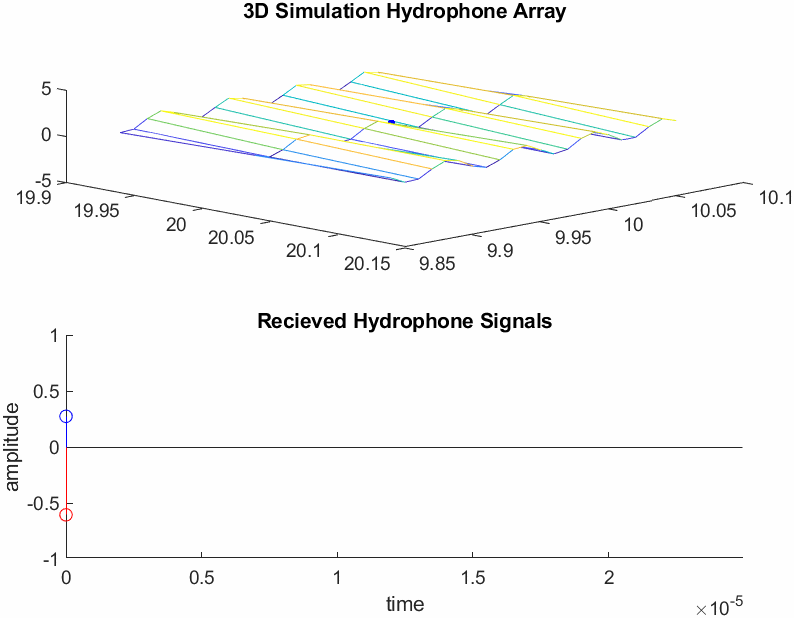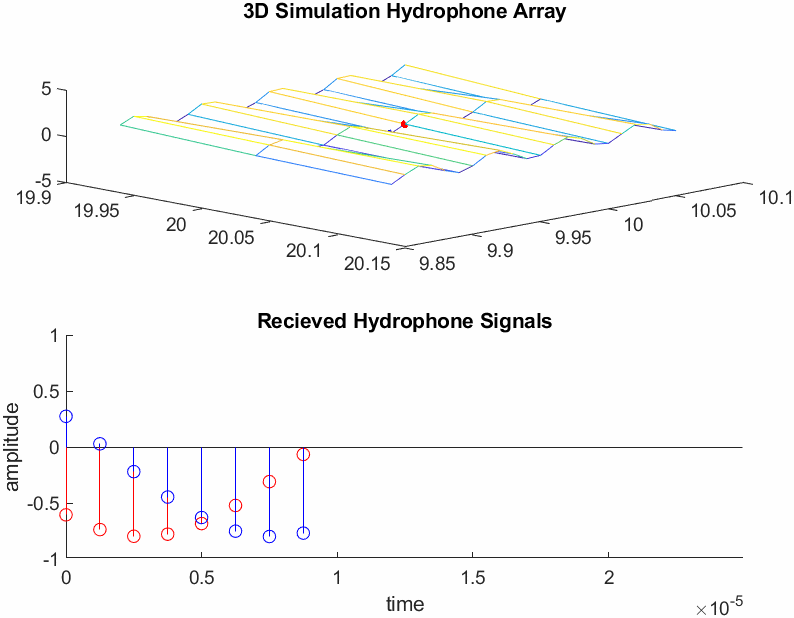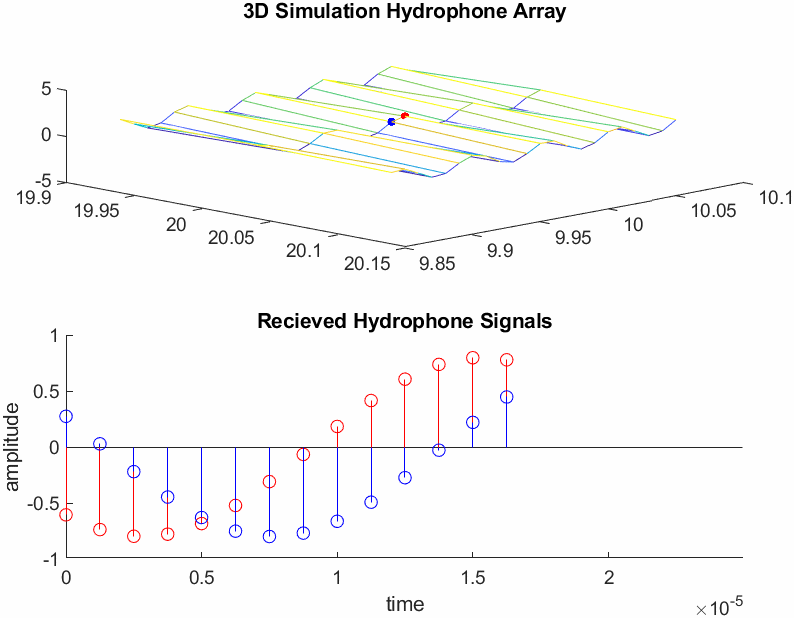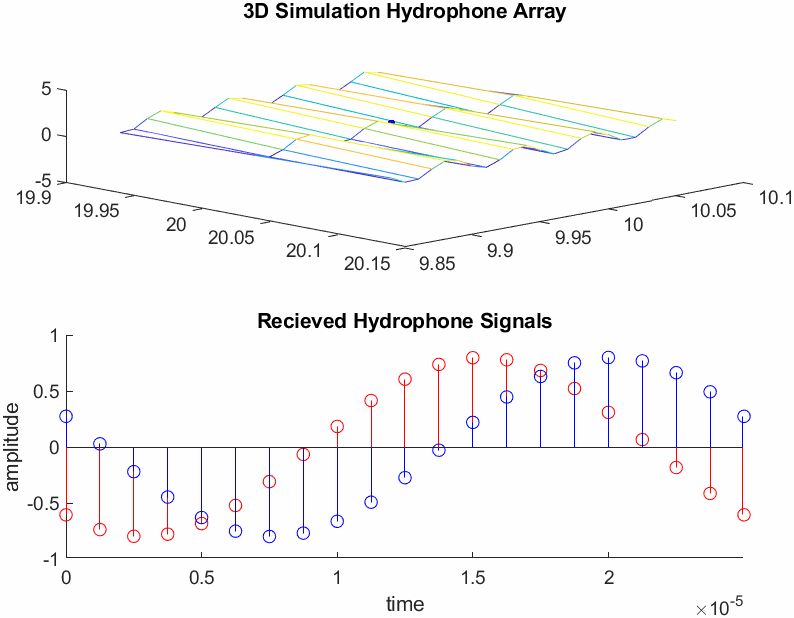
Equation (2.6) was then translated to MATLAB, and two hydrophones were placed on arbitrary points on the waveforms surface, seperated by 2cm. The hydrophones are represented by the red and blue dots in the upper image of Figure 3. As seen in Figure 3 the signals received by the hydrophones (bottom stem plot representing ADC samples) are phase shifted copies of one another.