Still Thursday or whatever, 21:22, 08/12/2022
Thursday, 16:41, 15/12/2022 - it took me an entire week to finish this incomplete project log.
Also, I will skip the part were I fix grammar mistakes, this Project Log is just so long that it is lagging the entire website for me.
Things to remember talking about in this project log:
- I think I need to focus first on creating a way of calculating a model of a McKibben muscle. Without that, all the following work is useless.
I asked on robotics stackexchange, but I got no answer until now. I asked on Quora and I only got useless asnwers.
I will try to ask on Researchgate (website for scientific articles that has contact with a lot of universities, no garantee that they will answer me without saying things like "just insert this equation in your super computer and you will get your answer").
We just need to ask around, eventually someone will give us an answer. - Discussing other options for McKibben muscle:
I can make the McKibben muscles out of Kevlar/Aramid, funny enough, these are kinda cheap online. I could use the third generation design of plated pneumatic muscles, but for hydraulics.
(I took a serious amount of hours trying to find the paper where they carefully explain how it is fabricated, but I couldn't find, I swear I had it on my PC, but I can't find it).
Also, I said it before, I don't know in which project log, but ROMAC artificial muscles are an interesting candidate.
For example, in the link I put in there, it is shown the romac lift 10,000 pounds (4535.924 Kg) with just 60 PSI.
But these are made of Aramid/Kevlar and are kinda difficult to fabricate.
Here is the patent and here is the stackexchange post where its fabrication is explained. - Hydraulic pumps and its relation to high pressure artificial muscles.
Let's say, something that achieves 12000 PSI, but can only flow 2 liters per hour, this could mean that the muscles can achieve much more strength without too much liquid flow. No? The amount of hydraulic oil inside a 1-5 ton hydraulic jack can fill up a single cup, but can lift 5 tons of mass. Could the same be applied to artificial muscles?
Unfortunately, I just got a small paragraph introducing to the concepts, I will calculate things more throughly in Project Log 16, it took me a week just to write this project log.
1 - Calculating Mckibben muscle:
As I'm writting this, I still don't have a correct answer, but someone on quora said I should use the "FPA triangle" equation for hydraulics.
I talk about that on "3 - hydraulic pumps an its relation to pressure and fluid flow", but here it is:
Basically, depending on what number you want to find (Force, Pressure or Area), you can use the equation "F = P x A" or "A = F ÷ P".
The problem is that it is a equation meant for hydraulic solid cylinders, not membrane actuators.
But I will try to use the area of the entire membrane, so I can somewhat calculate the force it will apply.
Accordingly to this cylinder area calculator, if I have a cylinder with 10cm radius and 30cm long, I will have a total area of 2513 cm2 (389.6 in²) applying 60 PSI (0,4 MPa), so I would have a force of 23340 pounds (10586,846 kg).
If it was 5cm radius 30cm length, I would have 1099cm² (170.3 in²).
- F = P x A
- 60 x 170
- 10200 pounds (4626,6422 kg).
This is the force applied to the area, but the area is the membrane, right? How to translate it to lifting force?
I'm still "asking around" on a crap ton of websites, so the correct answer will eventually appear.
Bruh, I started sending emails directly to authors from papers about McKibben modelling. I hope at least one of them answer my question...
And I also feel bad for some reason, like I'm interrupting something important they're doing to ask about a 5 ton hydraulic muscle because I'm too mentally challanged to understand their simple equations... y-y
Anyway, the worse it can happen is my emails being flagged as spam...
Edit³:
One week later, and finally someone answered me in this stackexchange question, I still didn't choose their answer as the correct one because you need to wait around 48 hours (accordingly to the mods).
And yes, it is definitely for a history about mechs, not for building real ones or anything like that... Hehe


Here is the rather large screenshot of what he wrote, see this a "TLDR".
Also, here is the copy paste of the text, because, my brother, I really don't want to lose this information:
Quoted from David Moews:
The McKibben artificial muscle is made from a cylinder of braided fibers closely surrounding an inner inflatable tube. When the tube is inflated, the cylinder of fibers expands in circumference, meaning that the length of the cylinder shortens.
One way to think of these muscles is that they operate like a lever: the product of the force put in and the distance you apply it over should equal the product of the working force taken out and the distance it acts over. In this case, the input force is given by the product of the gas pressure and the area it applies pressure to, which is the area of the braided cylinder, and the distance it works over is given by the increase in the radius of the cylinder; but this is not quite right because you also have to take into account the decrease in height of the cylinder.
Supposing that the cylinder has height h and volume V, is inflated with gas with pressure P, and is pulling with force F, the principle of virtual work says that:
PdV=−Fdh.
If the filaments that make up the braided cylinder have length S, wrap around the cylinder N times, and make an angle of θ from the vertical, then the circumference of the cylinder equals (S/N)sinθ, so its radius will be r=(S/(2πN))sinθ, and its height will be h=Scosθ. As the cylinder inflates, θ and r will increase from their initial resting values θ0 and r0 and h will decrease from its resting value h0, while S and N stay the same. A typical value of θ0 is 20∘.
Using the formula for the volume of a cylinder, V=πr2h, some mathematical work with the above equations gives you the formula:
F=Pπr20(3(cot2θ0)(1−ϵ)2−csc2θ0)
where
ϵ:=1−h/h0
is the fraction of the muscle's height which has contracted and is 0 at rest (1, (4), p. 19; 2, (7)). This means that you get less and less force as the muscle contracts, until at full contraction it exerts no force.
This formula does not take into account:
Friction;
stretching of the threads in the braided cylinder;
the non-cylindrical shape of the ends of the muscle;
energy used in deforming the inflatable tube;
or failure of the inner tube to fully conform to the braided outer cylinder.
After doing some experiments, Tondu and Lopez (1, (7), p. 20; see also Figure 7) decided that this formula would be more accurate with a fudge factor k multiplying the contraction:
F=Pπr20(3(cot2θ0)(1−kϵ)2−csc2θ0).(∗)
A typical value of k might be k=1.30. Given your specifications of P=800 kPa, F=49000 N of around 5 tons, taking k=1.30 and θ0=20∘ as above, and assuming you wish to exert the lifing force F even when the muscle has contracted by ϵ=0.2, solving for the radius using (*) gives a rather large value of
r0=71.1 mm
Accepting smaller maximum contraction factors of ϵ=0.1 or ϵ=0.05 would decrease r0 to 47.6 or 41.6 mm.
References:
1: "Modeling and Control of McKibben Artificial Muscle Robot Actuators", Bertrand Tondu and Pierre Lopez, DOI 10.1109/37.833638.
2: § 4.1.1, "Pneumatic Artificial Muscles: actuators for robotics and automation", Frank Daerden and Dirk Lefeber.
So my idea of using 10cm of diameter wasn't so wrong, after all...
BTW, this is at 0,8 MPa, I was planning things to be at 700 bars...
By the way I asked to https://chat.openai.com/chat, an AI chat that will write codes for you. I asked the AI to make a program on python that would give the result of the equation to see how much force the McKibben would generate, so I don't need to write a giant code every time I need to check a value on the scientific calculator.
(I use the code on "Spyder (Python 3.9)", which is more user friendly, if you don't know what this is, just search for tutorials on youtube, there are plenty, or just throw the code on python).
Just download it from GitHub.
Well, 5 days later and no answer yet, however, one single author was able to partially answer me, someone called "Alaa Al-Ibadi".
They said that "the disadvantage of a McKibben actuator is that when it is under load, even if it is under a load where the actuator is rated for it, the actuator will contract less than it should, so you will need to use a over-rated muscle for your 5 ton application".
Which is interesting and concerning. Interesting because I was already planning on making a muscle that is over that value for redundancy reasons and concerning because I would propably need an absolute unit of a muscle, similar to a fricking tree trunk.
They also said that I should read their article "Efficient Structure-Based Models for the McKibben Contraction Pneumatic Muscle Actuator: The Full Description of the Behaviour of the Contraction PMA".
Because "everything is explained there". Well, jokes on you, I'm stupid and I can't figure out. I literally found Alaa AlIbadi email through this hecking article.
On page 7 it is said that the equation "Pressure bar x Difference in volume ÷ Difference in length - Resistance force - Contactless forces = Force".
F = Pg ∆V/∆L − frs − fc
Which makes me go absolutely "bruh".
How do I calculate the change in volume? Doesn't the volume stay the same, but its shape just changes? The heck?
What do I do?

Well, let's start with the first equation:
The resistance force is defined as follows:
frs = sr Ain/∆L
where frs is the resistance force (N) of the rubber tube, sr is the stiffness (N/m) of the rubber tube, Ain (m2) is the inner area of the rubber cross-section, and ∆L (m) is the change of the actuator length between the initial length and length at each pressure step
Well, I couldn't find the fricking stiffness of the rubber tube, only this random image with values of polyurethane rubber springs that are much, much thicker than rubber tubes.
It is from this article: "Cyclic compressive behavior of polyurethane rubber springs for smart dampers".
Which would give 1,575 kN/mm = 1575 N/m, dunno if I should cut the value on half or...
- Sr = 1500
- Ain m² (I will use the cm² of the calculation I've made on F = P x A) = 0,1099
- ∆L (Well, I'm assuming this thing will contract in 20%, so it would be) = 6cm
- 1500 x 0.1099 / 6
- frs = 27.475
The losses force due to a contactless between the surfaces of the rubber tube and the braidedsleeve is found experimentally as shown in Equation (11):݂ =0.641ܮ∆
The losses force due to a contactless between the surfaces of the rubber tube and the braided
sleeve is found experimentally as shown in Equation (11):
fc = 0.641/∆L
Well, I don't have any idea on how to calculate that fricking number, so I will just copy it, lol.
- Fc = 0.641/6
- Fc = 0.10683333333
So...
F = Pg ∆V/∆L − frs − fc
"Pressure bar x Difference in volume ÷ Difference in length - Desistance force - Contactless forces = Force".
- Pg = 0,8 MPa = 8 bar
- ∆V (I don't fricking know, I will assume it will increase in volume by 20%). Accordingly to this Cylinder Volume Calculator, a cylinder with 5cm radius and 30cm length would have 2356.19cm³, so if it shortened by 6cm and increased its radius by 1cm, it would have 24cm of length and 6cm of radius 2714.34cm², and the difference is = 358.15
- ∆L = 6
- fts = 27.475
- fc = 0.10683333333
- F = 8 x 358.15 / 6 - 27.475 - 0.10683333333
- F = 449.9515 Newtons
- F = 45 kg or 10 lbs.

Ok, I need to find the correct f*cking stiffness of rubber tube. Hang on.
Well, I couldn't find the f*cking stiffness, but I will just divide it by 1000, f*ck it.
- frs = 1.5 x 0.1099 / 6
- frs = 0.027475
- Fc = 0.10683333333
- F = 8 x 358.15 / 6 - 0.027475 - 0.10683333333
- F = 449.9515 Newtons. Again.
Edit¹:
The own f*cking article of Alaa Albadi has it: 363.33N/m
- frs = 363.33 x 0.1099 / 6
- frs = 6.6549945
- Fc = 0.10683333333
- F = 8 × 358.15 ÷ 6 - 6.6 - 0.1
- F = 470 Newtons. Again.
What if I increase the pressure? 10 bar (1MPa)? 100 bar (10MPa)?
- 10 x 358.15 / 6 - 0.027475 - 0.10683333333
- 569.334833333 Newton = 58 kg = 127,99 lbs
- 100 x 358.15 / 6 - 0.02 - 0.1 (I took the enormous decimals alway because google wouldn't understand as a calculation).
- 5969.04666667 Newton = 608 kg = 1341,8 lbs
Wait, I calculated the change in volume in cm³, not in m³.
AGAIN:
- Pg = 1 MPa = 10 bar
- ∆V a cylinder with 5cm radius and 30cm length would have 0,002356m³, so if it shortened by 6cm and increased its radius by 1cm, it would have 24cm of length and 6cm of radius 0,002714m³, and the difference is = 0.000358
- ∆L = 6
- fts = 27.475
- fc = 0.10683333333
- F = 100 x 0.000358 / 6 - 0.027475 - 0.10683333333
- F = 0.13371166666 Newtons
Okay, it is worse.
Thanks, Alaa Al-Ibadi. You really helped me.

Ok, I will try AGAAAAAAAAIN
Referring to the assumption above for the Chou and Hannaford [11], the Tondu and Lopez [9] model, the type of material and its thickness and, as a result, its stiffness, plays a major factor in the force production. For that reason, the volume of the actuator is defined as follows:
V = 1 /4 πD 2 inL (8)
and:
Din = Dout − ThD
where V is the volume in m3 , Din is the inner diameter in m, L is the length of the PMA in m, Dout is the outer diameter in m, and ThD is twice the value of both the inner rubber tube and the braided sleeve thickness.
Figure 5 shows the cross-section of the actuator structure. From Equations (8) and (9) the volume of the PMA is less than the volume of the actuator in Equation (7). Moreover, the Win will be less and depends on the thickness of the rubber tube and the braided sleeve. Increasing the rubber tube stiffness leads to increase its resistance and the Wout will decrease, while the generated pulling force affects it longitudinally.
So...
- V1 = 1 ÷ 4π × 0.1^2 × 0.3
- V1 = 0.00235619449
I f*cking hope this goes somewhere.
- V2 = 1 ÷ 4π × 0.06^2 × 0.24
- V2 = 0.00006875493
- Volume difference = 0.00228743956
- F = 10 x 0.00006875493 / 6 - 6.6 - 0.10683333333
- F = -6.59725593407
Okay, now is definitive: Alaa Al-Ibadi was just screwing with me, lol.
Okay, AGAAAAAAAAAAAAAAAAIN.aaaaaa AaAAaAaaAAAAAAAAaaaAAaAAAAAAaaaaaaAaAAAAAaAAAaaaAAAAAaaaaAAAAAaAAAAAAaAaAAaAAAAAAaaAaAAaAAaaAAAaaaAAAAAaAAAAaaAAAAaaaAaAaAAaAAaAaaAaaA
Someone in another website said that I was calculating sutff in "radian" option on the calculator instead of the "degree" option.
So I decided to try again and:
- F = (10 x 0.00006875493) / 6 - 6.6 - 0.10683333333
- 470.8265 Newtons
- 105,84600821 lbs or 48,0109417190134 kg
F*ck
I did the same with that equation from Project Log 11:
First I tried the same equation and then I got happy.
- ((π(4.97))²(100 ÷ 4 (sin(45))²))(3(1 - 0.11 ÷ 24)² cos(45)²2 - 1)
- And it gave 6011.09266712
Then I tried:
- ((π(4.97))²(100 ÷ 4 (sin(45))²))(3(1 - 0.11 ÷ 24)² cos(45)²x2 - 1)
- It gave 15069.5367261
Then I tried:
- ((π(4.97))²(100/4 (sin(45))²))(3(1 - 0.11/24)² cos(45)²(2 - 1))
- It gave 9058.444059
F*ck you McKibben.

Ok, let's try agaaaaaaaaaaaaaaaaAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAain.
I literally forgot what all those symbols in the equation on Project Log 11 means, so I will read and relearn everything.
AGAAAAAAAIN!!!!!@!@@!1@!@!@!!!@!@!@!@!@!@12
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
(YOU BETTER READ THIS THING UNTIL THE END, BECAUSE I'M GIVING MY BEST, EVEN THOUGH IT IS NOT ENOUGH)

First, let's define the values (guess what? When you change a value in inches to cm, the equation doesn't work):
- Lengths are in mm.
- Pressure is in MPa
So, the equation:
- P1 = 0.
- L1 = 300mm.
- D1 = 100mm.
- 01 (the weird zero) is about the braid angle, I don't know yet, I will just use the angle that normally is used on conventional braided sleeve, something between 18 and 11 degrees.
- P2 = 1 MPa
- L2 = Since these normally compress to around 20%, it will be: 240mm
- D2= I also don't know, I will just throw 20%: 120mm
- 02 = 30º degrees, whatever.
- ∆L (difference in length) = 60mm
Now let's try to calculate (and yes, I put it in "degrees" instead of "radian" (and unfortunately, there isn't [ on google calculator:

- (π × 100^2 × 1 ÷ 4 × sin(15)^2)(3(1 - 6 ÷ 300)^2 cos(300)^2 - 1)
- -147.154927431
You gotta be f*cking kidding me.
Let's try on radian:
- (π × 100² × 1 ÷ 4 × sin(15)²)(3(1 - 6 ÷ 300)² cos(300)² - 1)
- -3316.57453819
Ok, maybe there is something wrong with what I wrote... In the original equation it has a ² after a Sin, but when I insert a Sin on the calculator, it immediatly asks me to put something between ( ).
- ((( (π(100²) ) 1) ÷ 4) (sin(15)²)(3(1 - (6 ÷ 300))² cos(300)² - 1)
- -147.154927431 AGAAAAIN

I was writting 6 instead of 60
bruh
- ((( (π(100²) ) 1) ÷ 4) (sin(15)²)(3(1 - (60 ÷ 300))² cos(300)² - 1)
- -273.580844705
- Radian = -3318.13325269
...?
Okay, again:
- ((π × 100^2 × 1) ÷ 4 sin(15)^2)(3(1 - 60 ÷ 300)^2 cos(300)^2 - 1)
- -273.580844705
- Radian = -3318.13325269
Maybe I should put that dot between the 4 and the sin?
- (π × 100 × 1 ÷ 4. sin(15)^2)(3(1 - 60 ÷ 300)^2 cos(15)^2 - 1)
- 4.16360787029
- Radian = 3.58964975856
Oh, I was typing cos(300) instead of cos(15), let's try:
- (π × 100 × 1 ÷ 4 sin(15)^2)(3(1 - 60 ÷ 300)^2 cos(15)^2 - 1)
- 416.360787029
huh?!
I tried an online scientific calculator:

Uuuuh, is this normal?


The result seems like 1308.infinity.
Edit²:
Just now I noticed that I forgot to put a ")" between the 3 and the first equation, maybe that's why it got all messed up.
Yeah, it was that, it gave the same 416 newtons
But this little calculator made me realize something: maybe the calculator is calculating everything at once instead of one step at a time.
So I will try AGAIN, this time one ( ) at a time:
- π × 100^2 × 1 ÷ 4 sin(15)^2
- 526.117009048
- 3(1 - 60 ÷ 300)^2 cos(300)^2 - 1
- 0.79138438763
- (526.117009048) (0.79138438763)
- 416.360787027
Ok, this result seems true since I'm seeing it by the second time.
Wait, why does I barely see the values of the actuated muscle in this equation?
Is the pressure in the first ( ) the pressure at rest? Let's make it zero:
- (π × 100² × 0 ÷ 4 sin(15)^2)(3(1 - 60 ÷ 300)^2 cos(15)^2 - 1)
- It actually gives 0.
- huh...
I wonder what if I increase it to 68,94757 MPa (10000 PSI)
- (π × 100 × 68.94757 ÷ 4 sin(15)^2)(3(1 - 60 ÷ 300)^2 cos(15)^2 - 1)
- 24749.7628004
Hum, so it does increase with increase in pressure... 🤔
416,360787027 Newtons is 93,6 pounds or 42,4.
24749,7628004 Newtons is... I don't know, the converters just give an error message. 👀
I had to convert Newtons to KiloNewtons, then convert to other values.
- 24749,7628004 Newtons
- 24,7 KiloNewtons
- 5552,7 pounds
- 2518.7 kg
humm... Interesting, I feel like I'm on something.
And I also feel like Hackaday is lagging too much, maybe the draft is too heavy? 👀
Now trying the second equation:

- F= (πD1²P/4) (3cos²0-1)
- (π × 100^2 × 1 ÷ 4)(3 cos(15)^2 - 1)
- 14129.6122408
- Radian = 5744.22289863
There is something wrooooooooong and I don't what it iiiiiiiiiiiiiiiiiiiiiiiis...
Trying each one separatedly:
- π × 100^2 × 1 ÷ 4
- 7853.98163397
- 3 cos(15)^2 - 1
- 1.79903810568
- (7853.98163397) (1.79903810568)
- 14129.6122408
Doing again, but in radian:
- π × 100^2 × 1 ÷ 4
- 7853.98163397
- 3 cos(15)^2 - 1
- 0.73137717483
- (7853.98163397) (0.73137717483)
- 5744.22289862
NOW I get it, I'm inputting the angle of the unactuated muscle, I need to put it actuated.
- (π × 100^2 × 1 ÷ 4)(3 cos(30)^2 - 1)
- 9817.47704247
- Radian = -7293.36026722
- huh?!
huh?!

Well, this is taking too long, no one is being able to answer me, I literally offered money on some websites that are specifically meant for hiring engineers/roboticists etc.
I mean, I started the announcement yesterday, so maybe I'm being a little impatient.
Anyway, taking the most realistic value we got until now, the 614 newtons of force, I will try to extrapolate a possible dimension that such artificial muscle would have in order to lift 5 tons.
So, just to remember (because I'm taking days between these line spaces, btw):
- (π × 100 × 1 ÷ 4 sin(15)^2)(3(1 - 60 ÷ 300)^2 cos(15)^2 - 1)
- 416.360787029 Newtons
- 93,6 pounds
- 42,4 kilograms
- waaaaaaait a minute, I forgot to put ² after the diameter
(forget it, it gives the same result).
I could increase the pressure until 10,000 PSI or 69 MPa (nice), however, as shown before, this would still not be enough, I would "only" get 2 tons out of this muscle.
Not to mention that the more pressure I need, the more energy I need to spend, specially since we are talking about 72 muscles (or more).
Even though they would not be fully actuated all the time, but what is the point of having a mech if it won't be working "full throttle"?
So I need to increase its radius or its length, but I don't want to increase its length, because it simply wouldn't fit inside its body, lol.
So, let's try to increase its diameter by more 10cm, a trunk of a muscle.
- (π × 200^2 × 1 ÷ 4 sin(15)^2)(3(1 - 60 ÷ 300)^2 cos(15)^2 - 1)
- 1665.44314812 Newtons
- 374,4 pounds
- 169,8 kg
- Pressure is 1MPa = 1 Bar = 145 PSI
Now let's increase the pressure to 8 MPa (or 1300 PSI):
- (π × 200^2 × 8 ÷ 4 sin(15)^2)(3(1 - 60 ÷ 300)^2 cos(15)^2 - 1)
- 13323.5451849 Newtons
- 2995,2 lbs
- 1358,6 kg
Frickty frockty fruckty, this doesn't seem good.
let's try 30 Mpa (or 4000 PSI)
- (π × 200^2 × 30 ÷ 4 sin(15)^2)(3(1 - 60 ÷ 300)^2 cos(15)^2 - 1)
- 58083.3177989 Newtons
- 13057,6 pounds
- 5922,8 kg
- (I have to rewrite the f*cking equation everything on the calculator btw, y'all are just skipping the boring part)
Bruh, dunno about that, 4000 PSI? This seems a little too much.
And I still didn't calculate the amount of liquid everything would have.
So, let's do it now:
- Just like in Project Log 12, we will use the pipe volume calculator, our "pipe" being the McKibben muscles with hydraulic oil, obviously.
- Innerd diameter is 20cm, the length is 30cm, the oil density is 8 g/ml.
- A single McKibben muscle would have 9.4 liters of volume and 7.54 kg of mass.
- Since there are 72 of those, everything would weight:
- 676.8 liters of volume and 542.88 kg of mass.
You know, I thought it would already reach 2 tons or something... Interesting. This seems viable. Specially if you take into consideration the fact that I will fill the muscles with something and then insert the hydraulic oil.
🤔 hum...
I will just try the other equation, with the 10cm diameter, but with 700 bar (or 70MPa or 10152 PSI), because the hydraulic hand pumps are normally rated in that pressure.
- (π × 100^2 × 70 ÷ 4 sin(15)^2)(3(1 - 60 ÷ 300)^2 cos(15)^2 - 1)
- 29145.255092 Newtons.
- 6552,0566691191825 pounds
- 2971,9 kg
Well... Sadge.
But IF the next muscles aren't as easy to calculate, I think I would still stick with the 10cm in diameter McKibben muscle, because these results are a guess, not a precise calculation/simulation of the artificial muscle.
For example, I'm assuming that the braided sleeve will have 15º degrees of angle, and when actuated it will shorten by 6cm and the angle of the braided sleeve will change to 30º degrees. Which could be either shorter than what it will actually actuate, or longer than it will actually actuate.
I will need to buy the pump and the material to make one by hand, and these calculations are only pointing where I should go.
For example, for some reason the equation uses the initial angle, not the final one.
So, if I change the initial angle to either 20º, 30º or 11º degrees:
- (π × 100^2 × 70 ÷ 4 sin(20)^2)(3(1 - 60 ÷ 300)^2 cos(20)^2 - 1)
- 44722,661559700005455 Newtons
- 10054,05 pounds
- 4560,44 kg
- (π × 100^2 × 70 ÷ 4 sin(11)^2)(3(1 - 60 ÷ 300)^2 cos(11)^2 - 1)
- 17015.8574881 Newtons
- 3825,31 lbs
- 1735,13 kg
- (π × 100^2 × 70 ÷ 4 sin(30)^2)(3(1 - 60 ÷ 300)^2 cos(30)^2 - 1)
- 181426.975745 Newtons
- 40786 lbs
- 18500 kg
Wouldn't 11º braided sleeve allow for more change in the angle once actuated?
Also, the calculator starts giving negative numbers if you insert any amount of degrees bigger than 40º.
- (π × 100^2 × 70 ÷ 4 sin(40)^2)(3(1 - 60 ÷ 300)^2 cos(40)^2 - 1)
- 28781
- (π × 100^2 × 70 ÷ 4 sin(50)^2)(3(1 - 60 ÷ 300)^2 cos(50)^2 - 1)
- -66686.9814423
- (π × 100^2 × 70 ÷ 4 sin(60)^2)(3(1 - 60 ÷ 300)^2 cos(60)^2 - 1)
- -214413.698608
(and yes, every single calculation you see here I had to write using the mouse, because I don't know how to automatically change the google calculator research to "degree" instead of "Radian")

Is as if it is mocking me...
Also, the "cost of weight":
- 10cm diameter, 30cm length, 0.8 g/ml, you know the drill
- 2.3 liters of volume, 1.88 kg of mass
- 169.632 liters of volume in total and 135.36 kg of mass in total.
- Again, I will fill the inner tubing with something (silicon foam, maybe?), so it would weight even less.
Also, I just found this webpage about McKibben muscles about a knitted one.

Yes, knitted, like your grandma does it.

Meaning that I don't need to make a sleeve as small as the one shown in conventional McKibben muscles that normally uses nylon braided sleeve.
Which means they can be stronger.
I think.
2 - Discussing other options for McKibben muscle (ROMAC and PLEATED):
Well, I will start with the Plated, because it is the simplest to build (I think).
Here is the link for the all 3 generations of Pleated Pneumatic artificial muscles.
However, I still couldn't find the method of fabrication, not that it would make too much of a change, since the blueprints and 3d models aren't available, but it is kinda frustrating still.

uuuuuuh...
I've been looking at these pdfs for the past 2 days and I can't make heads out of this crap.
Funny enough, the third generation has the simpler explanation for the second and first generation of Pleated Artificial muscles. I will try now how to calculate this crap.
(also, you have no idea of how many times I wrote "I give up" throughout this project log and went back to erase it)
Since the design of the membrane has not changed, the same mathematical model is assumed for PPAM 3.0 and validated in this section.
As derived in the generated force F equals:with f(e,l0/R) the dimensionless force function as defined by Daerden. The contraction is defined as e = L0-L/L0, L0 is the maximum length of the muscle’s membrane and R represents the minimum muscle, radius.
- F =pL0²n/2π sin(2π/n)f(e,L0/R)
L0/R is called the slenderness, p is the relative pressure inside the muscle and n is the number of fibres used. This function f depends only on contraction and geometry as far as the elasticity of the fibres is neglected. The thicker the muscle, the less it contracts and the higher the forces it generates in short contractions. Contraction can reach up to 30 54% in a theoretical case with l0 L0/R = ∞, which is bounded in practice because of minimum space needed to fold the membrane.
Static load tests on real muscles were carried out to validate the proposed mathematical model of Equation (1). Four standard muscles were tested on different contraction trajectories between 150 N and 3 KN with a test bench at isobaric conditions, while applying three different gauge pressures: 1–3 bar. The tested muscles are made with 32 pleats, have a maximum membrane length l0 = 110 mm and unpressurized radius of 15.6 mm at the top of the polyester fabric pleats and R = 11.5 mm for the position of the Dyneema fibres.

So, let's get going with the same procedure:
First figuring out the units of measurement, then listing what the f*ck (I think) each symbol represents:
- Distance units is mm, Pressure gauge seems to be in bar. Or not?
In page 8 as quoted:
The coefficients of the fitting process for the force function of the third generation PPAM, following the structure of Equation (2), are given in Table 1. The values are valid when the generated force F is expressed in N, the initial muscle length l0 in m, the pressure expressed in bar, and the contraction E expressed in %.
- Also, in the first article that this paper refers to, they use pressure in kpa and cm.
- You can read the first one here: "THE CONCEPT AND DESIGN OF PLEATED PNEUMATIC ARTIFICIAL MUSCLES".
Well, I will try to calculate in both ways.
- p = 10 bar (or 1000KPa).
- L0 = maximum length, maybe the initial length? = 300mm (or 0,3 meters or 30cm).
- n = dunno, let's use the example given = 32
- f = What the f*ck this little "f" is supposed to mean? It is force? I was reading the first document and it seems to be "Dimensionless force function", and it is something related to the contraction ratio, since I'm assuming this wil have 20% of contration = 0.5
- R = radius = 50mm (or 0,05 meter or 5 cm).
- e = L0-L/L0 = what the f*ck is the L?) =
Well, this is already going down hill, but let's try this stupid calculation with each set of units.
- First mm and bars
- Second KPa and cm
- third bars and meter and %.
- F =pL0²n/2π sin(2π/n)f(e,L0/R)
- I don't f*cking know why the "e" is separated by a comma, I can't add that on the calculator.
- e = L0-L/L0
- e = 300 - 300/300
- e = 299
- 10 x 300² x 32 / 2π sin(2π/32)0.5(299 x 300/50)
- 139062878.719
- 31262578,8 pounds
- 14180467,25 kg
- ????
Maybe if I put a dot between the 299 and 300?
- 10 × 300^2 × 32 ÷ 2π sin(2π ÷ 32) × 0.5(299.300 ÷ 50)
- 464008.022304 Newtons
- 104313,15 pounds
- 47315,65 kg
This number seems too high. I will try to change the L = 240 and instead of a comma, I will add a "e" from the calculator to see what happens
- 10 x 300² x 32 / 2π sin(2π/32)0.5(e300/50)
- 72436589.0034 newtons
- 16284393,07 pounds
- 7386476,44 kg
- e = L0-L/L0
- 300-240/300 = 299.2
- 10 x 300² x 32 / 2π sin(2π/32)0.5(299.2x300/50)
- 139155897.367 newtons
- 31283490,3 pounds
- 14189952,5 kg
- 10 x 300² x 32 / 2π sin(2π/32)0.5(300/50)
- If I take off the "e" value it doesn't change much though:
- 465093.239864 newtons
- 104557,12 pounds
- 47426,3kg
Now, let's try kpa and cm:
- F =pL0²n/2π sin(2π/n)f(e,L0/R)
- e = L0-L/L0
- e = 30-33/30
- e = 29
- 1000 x 30² x 32 / 2π sin(2π/32)0.5(29x30/5)
- 13487703.9 newtons
- I tried to add the "e"
- 1000 × 30^2 × 32 ÷ 2π sin(2π ÷ 32) × 0.5(29e × 30 ÷ 5)
- 36663380.5714
- 1000 × 30^2 × 32 ÷ 2π sin(2π ÷ 32) × 0.5(e × 30 ÷ 5)
- 1264254.50246
- I won't even give the effort of converting the number, it is just damn high.
And without the e:
- 1000 × 30^2 × 32 ÷ 2π sin(2π ÷ 32) × 0.5(30 ÷ 5)
- 465093.239864 newtons
- 104557,1 pounds
- 47426,3 kg

Dunno who this guy is, but dayum, what a marvelous beard, the drip, the style.
Now that we are in the third, let's try with bars, meters and %.
- F =pL0²n/2π sin(2π/n)f(e,L0/R)
- e = L0-L/L0
- 0.3-0.3/0.3
- e = -0.7
- 10 x 0.3³x32/2π sin(2π/32)0.5(-0.7%0.30/0.05)
- -0.00325565267
Ok... what if the percentage is 29%?
- 10 × 0.3^2 × 32 ÷ 2π sin(2π ÷ 32) × 0.5(29% × 0.3 ÷ 0.05)
- 0.13487703956
- Now it is too damn low!
What if I put 0.29%?
- 10 × 0.3^2 × 32 ÷ 2π sin(2π ÷ 32) × 0.5(0.29% × 0.3 ÷ 0.05)
- 0.00134877039
Wait, I forgor to insert the pressure in KPa:
- 1000 × 0.3^2 × 32 ÷ 2π sin(2π ÷ 32) × 0.5(0.29% × 0.3 ÷ 0.05)
- 0.47956280732
What if it is cm with bar and mm again?
- cm:
- 10 × 30^2 × 32 ÷ 2π sin(2π ÷ 32) × 0.5(29% × 30 ÷ 5)
- 1348.77039561 newtons
- 303,2 pounds
- 137,5 kg
Seems ok now.
- mm:
- 10 × 300^2 × 32 ÷ 2π sin(2π ÷ 32) × 0.5(299% × 300 ÷ 50)
- 1390628.78719
Ops, put 299%, not 29%
- 10 × 300^2 × 32 ÷ 2π sin(2π ÷ 32) × 0.5(29% × 300 ÷ 50)
- 134877.039561 Newtons
- 30321,5 pounds
- 13753,6 kg
It still seems too damn high...
Wait a minute... In the article it is said that the pressure gauge is 0.5 bar (0,05 MPa), maybe this muscle is that strong, huh?
- 0.5 × 300^2 × 32 ÷ 2π sin(2π ÷ 32) × 0.5(29% × 300 ÷ 50)
- 6743.85197803 Newtons
- 1516,07 pounds
- 687,68 Kg
Trying to remove the "e" thingy:
- 0.5 × 300^2 × 32 ÷ 2π sin(2π ÷ 32) × 0.5(300 ÷ 50)
- 23254.6619932 newtons
- 5227,8 pounds
- 2371,3 kg
I'm doing something wrong, or this muscle is just too overpowered?
I can't even replicate their results using the same numbers they provide...
Well, I couldn't find the modelling (aka force calculation, whatever I've been doing here), so I think I will be forced to skip it.
I can only find this old as heck document that dates from 1980.
But I think that is for teh better, as you can see from this illustration from its own patent, it seems that ROMAC actuators are flat actuators.
Meaning that I would need to fill and empty their entire inner volume in order to actuate and unactuate them with hydraulic oil, which would need too much energy and oil flow.
3 - Hydraulic pumps and its relation to pressure and fluid flux/flow:
Well, I will start writting this one (even though it will be the third one for the reader), because I actually found a lot of materials about it.
I will avoid inserting the video player here because there is a lot, and these would eventually make the Project log too long.
- "Do Pumps Create Pressure or Flow?"
It is a simple and visual video explaining about flow and pressure, in certain cases the pump only produces flow, and in certain cases it only creates pressure. - "Pascal's Principle, Hydraulic Lift System, Pascal's Law of Pressure, Fluid Mechanics Problems".
It is a video explaining the basics of hydraulics, it may be useful for calculating McKibben muscles or other types.
Like, you could calculate the volume inside a cylinder (the initial state of the McKibben) and the volume inside a bigger cylinder (the actuated state of the McKibben muscle) and guess your way into finding how much weight it would be able to generate. - "Troubleshooting".
This is actually a playlist of videos explaining hydraulic principles in a simple manner, I'm still half-way through.
In this video of the playlist they explain a "triangle" to help calculate the force applied. In the case of a hydraulic cylinder (not a muscle), it is pressure x surface area = force.
I don't know yet if it will be useful for muscles, but... - "Fluids in Motion: Crash Course Physics #15"
This is video about fluid dynamics, basically it explains that if there is 1 kg (or liter) of water flowing in a second in a wider tube, it will also have the same 1 liter per second flow in a narrower tube, but in a longer section.
It also says that the slower the fluid, the more pressure it applies to the tubing, and the faster the fluid, the lower the pressure it applies to the tube that contains it... Dang. - "Water pressure versus water flow"
It is a short video, it shows that even though he limited the water flow by half, the pressure inside of the tube keeps at 7 bars. - "Velocity and pressure"
The same as the previous two videos, but a little bit more visual.
I just remembered about a series of "walking trucks" that the US tried to develop during the 60's, there are a lot of interesting designs, but the fact that we don't have one in use today is telling of its effiency and practicality.
The entire contraption weighted around 3000 pounds (1400 kg) and used 50 gallons per minute of hydraulic fluid, which was feeded by an external power source.
50 gallons is a similar number of what I calculated in previous Project Logs for the amount of hydraulic fluid the humanoid mech would use.
Although 63 liters per second is 3780 liters per minute, which would be 998 gallons per minute...
Something must be terribly wrong with my calculations...
Also, the driver sit (or standed) 15 feet from the ground, almost 4 meters tall. Operating 4 limbs all at once.
Which is also telling that maybe this mech project could be viable in some way, after all it would weight and stand at almost half (or less) of what this walking truck had.
Although the mech was made to have as little as moving parts as possible, the tip of the feet is more important than you might think.
I'm not trying to say that I know more than the motherhecking engineer that made this marble of engineering 80 years ago, but the tip of the feet is the only mechanical lever in the body (that I could find) that actually has mechanical advantage.
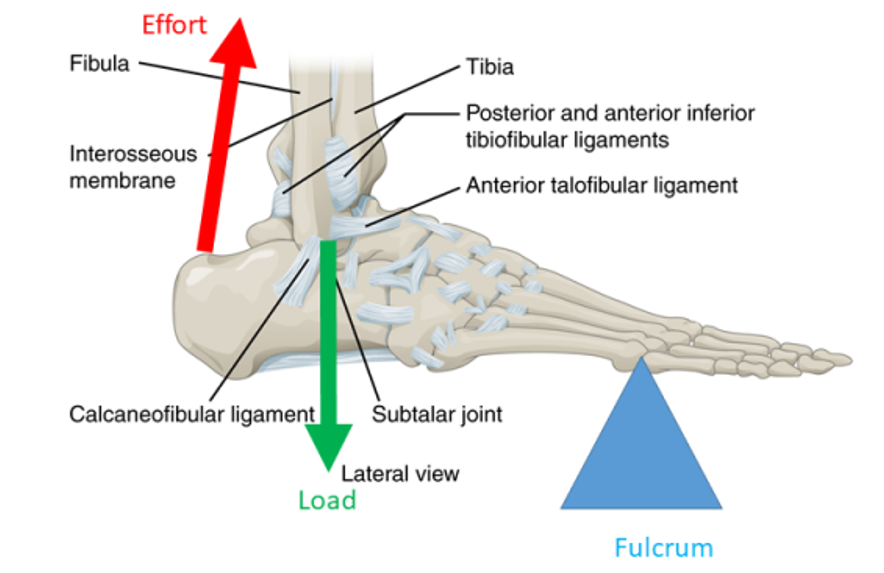
As you can see, the lever effort is far away from the fulcrum than the load lever, this "load" being the entire weight of the body.
Of course, this is for the pulling force of a muscle, not the pushing force of a hydraulic cylinder. Even then, you could make some mechanism to do that.
Also, you could easily increase the lever, and thus the mechanical advantage of the feet. It would look weird to see a feet longer in the back than in the front, but whatever.
Not that this is somekind of detail that will "save the walking machines" or whatever, it is just a little help that maybe can help a lot.
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.
Regarding your third-to-last paragraph, hydraulic (and pneumatic) cylinders can be used for pulling, too. In fact, in most applications, they do both.
Are you sure? yes | no
Yes, it is true, I was not taking that into consideration because I was thinking of using cheap hydraulic jacks that normally doesn't have that function.
Which would sound really weird, since my smooth brain didn't thought on actually writting it. lol
Are you sure? yes | no
I do wonder if the line where you wrote x kN/mm = y N/m has something to do with the equations not working.
I believe x kN/mm = y meganewtons per metre.
Are you sure? yes | no