Sunday, 08:24, 26/02/2023
Edit⁵:
Well, guess who made mistakes AGAIN?!
So, I made this project log with the idea that 10mm McKibben muscle can output 200 lbs of force because of the Hackaday video.
The thing is that I missremembered it, and in fact, the McKibben muscle that can actually output 200 lbs of force is the 1 inch braided sleeve muscle.
1 inch = 2.5 centimeters.
2.5 centimeters = 25 milimeters.
4:47 is the time mark of the moment I mistaken for something else.
So, this mean I will have to remake the entire calculation because I'm stupid. :|
25mm in diameter, 30cm in length, 0.147-150 liters inside when unactuated, 0.290 liters actuated, 0.140 liters of difference.
Like I said in previous edits in this same Project Log (actually, I didn't), I would need in 564 muscles in total for the first configuration of simply multiplying all lower limb muscles quantities by 3.
84.6 liters in total, 253.8 liters per second if it was a third of a second, 15,228 liters per minute.

If I actuated only the bottom half, I would need 9720 liters per minute in total, 4860 LPM.
Needing 61 hydraulic pumps, needing 48.6 hp of power.
The top half would need 2754 LPM, 35 pumps, 27 hp of power.
If the 6 bundles of muscles on the thighs and feet where enough, then...
+6 on the hips/thighs, +6 on the feet/ankle of bundle of muscles with 3 muscles each. 36 muscles in total.
+3 groups on the top part of the knee, +3 groups on the opposite side of the knee. 18 muscles in total.
Now, the top of the body, +6 for the torso, +6 for a neck, +6 for the shoulder, +1 for moving the arms up, +1 to move the arms down, +1 for the biceps, +1 for the triceps, +6 for the wrist, +3 per finger.
31 muscles for each arm alone, +6 (the neck doesn't need to be that strong, so I won't count it), 68 bundle of muscles in total.
So, since each muscle bundle has 3 McKibben muscles, then it is 204 muscles in total, 5520 liters per minute, 2760 liters per minute if only half was actuated.
If I used only 80 LPM hydraulic pumps, I would need around 35 of those, and since each pump needs 0.8 hp to run at 8 bars, I would need 27 hp.
Assuming it is still 10mm braided sleeves, but at twice the pressure, so they supposedly output twice the amount of force, so I don't need the same amount of fluid flow, I would need around 44 hp of power in total for 28 pumps.
Well, since my last post, I will now have to calculate a more... Reallistic and easier approach for the actuators.
And at least this time it maybe won't be as labor intensive as making a 30cm per 15cm McKibben muscles out of multifilament steel cables as I was planning on doing, lol.
I will now calculate how many of those I would need, the power requirement and the cost.
- Conventional McKibben muscles
- Multifilament McKibben muscles
- Homemade hydraulic cylinders made of PVC or Metal.
Edit²:
I think that this edit is important enough to be mentioned.
I don't actually need 1.25 hp per pump to achieve 4 bars of pressure, I miss calcualted it.
I actually just need 0.4 horse power to achieve 4 bars. :|
And yes, I did remade some calculations, 0.4 hp is around 3 times less horsepower than 1.25.
So even though I misscalculated, needing 40 hydraulic pumps or more is still an insane amount of pumps to feed.
By the way, something that I forgot to talk about, since I will make a 300 kg power mechsuit that will only be able to lift 100 kg, this means this suit will be as strong as the Guardian XO.
Except it won't cost 100,000 euros. :|
Now that I think about it... 100-300kg is more or less on the capacity of a well trained human being.
I guess that of all things, that phrase of captain america movie kinda makes sense for exoskeletons: "it doesn't give you anything, it simply augments what is already in there" (I think that's what the doctor said or whatever).
It is an "augmentation suit", yes, I will build it with its own skeleton for self support, but it would be an outstanding piece of equipment if I were already buffy enough.
But will I train to be strong enough to be an outstanding piece of equipment? Hell no. xD
Also, I think in this case Passive and Quasi-passive exoskeletons/exosuits could be a fine adition in order to take alway the maximum weight as possible from the wearer.
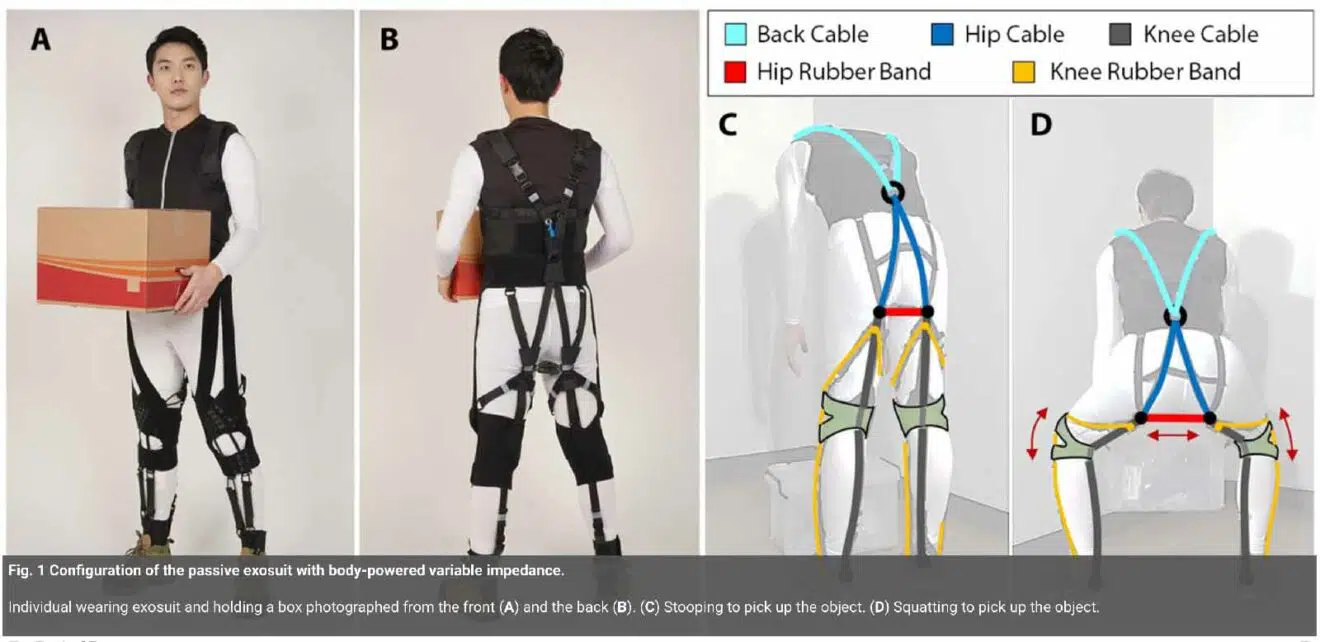
There are a lot of those passive and quasi-passive exoskeletons, after all, these are really cheap and simple to make.
I remember reading about one some years ago saying that "exoskeletons and exosuits differ where exoskeletons are rigid suits and exosuits are soft suits", the above image is an exosuit.
The rigid ones are more like orthopedic auxiliary devices, and to be honest, that is a good enough reason to research exoskeletons on its own.
I remember seeing once an article about a quasi-passive exoskeleton where there was a rubber air pump (like those used for measure blood pressure bags) on the user's foot, and every time they stepped on the ground, the air/liquid pump would fill up low pressure McKibben muscles.
I think it is this one, if I'm not mistaken.
... No, by the sound of it, it is a pneumatic activated muscles.
The one I saw was a muscle used on the thighs not on the ankle/feet... hum...
I remember downloading an article about it once, but it is buried between the 30+ gigas of scientific articles I have on my pen drives, lol.
1- Calculating McKibben muscles.
Starting with conventional hydraulic McKibben muscles with stainless steel or aramid braided sleeve, which is actually hard as heck to find on the internet.
In fact, I think it is impossible, because I couldn't find a single website selling those things, only copper painted in silver.
Ok, 2 hours later I finally found those, and normally these are more or less 60 reais (11 dollars) per meter or in packs around 300 reais (50 dollars) with 10 meters or so.
Goddammit, that's why I wanted to make then by hand using steel cables. Just now I remembered why. >:(
And normally, these are for 20mm braided sleeves, while nylon sleeves, I can easily find up to 50mm of diameter.
The ones used by HackSmith were 3/8 inch, which is more or less 10mm (1cm) of diameter.
Which is interesting, because I'm aiming for 2-5 times bigger than that. 🤔
Dunno if I can say that the strength will also be 2-5 times higher than those they used...
So, let's go with 10mm and then 20mm and 50mm.
But beforehand: let me say that this is if all muscles were actuated at once, it wouldn't happen.But it just gives an idea.
I will cut in half or at least in a third more or less what one would need.
Also, combustion engines don't actually stay at its ranged horsepower (like 400-500) all the time, only in certain moments, like climbing a hole, a ramp etc.
So the average hp would be way bellow that.
For 10mm McKibben muscles:
- 10mm in diameter
30cm in length
0.024 liters (24 ml)
and weight 0.02 kg (20 grams)
- 72 bundle of muscles each containing 3 unactuated mckibben muscles will have in total:
5.1 liters of volume
4.32 kg.
- Contraction reduces length in 20% and increases diameter in 40%.
14mm in diameter
24cm in length
0.046 liters
and weight 0.05 kg - 72 bundle of muscles each 3 actuated McKibben Muscles will have in total:
9.9 liters
10.8 kg
- The difference is what I will have to pump in a second or less:
4.752 liters
6.48 kg - 4,752 liters per second
285,12 liters per minute - I would need around 4-5 hydraulic pumps running at 1750 rpm, 1.25 hp each.
I would need around 5-7 hp engines.
- 14,256 liters per second if pumping in a third of a second.
855,36 liters per minute. - I would need 17 hydraulic pumps running at 1750 rpm and 1.25 hp each (4 bars of pressure).
I would need a 21.25 horsepower engine.
*Like I said in the beginning, it is actually 0.4hp, so I would still need around 6.8 hp.
And since there are pumps with 130 liters per minute, I would actually need 7 pumps each running at 0.4hp, which would require 2.63 hp in total.
- Always good to remember that this is just the value necessary inside the muscles, the fluid inside the hoses, fluid tank and so on would increase the liters per second significanly.
- Also, 10mm nylon braided sleeve costs around 6 reais (1 dollar) per meter.
And since I would need 64,8 meters in total, this would need to pay 388.8 reais (around 75 dollars).
If it was Aramid/steel braided sleeve, it would cost 1944 reais (370 dollars).
Well, even though I would make a homemade pump, I doubt the amount of horsepower, torque and rpm would change much, simply because of the thickness of the fluid.
Also, remember that I'm thinking on usind LDPE as the inner bladder since it is cheaper, doesn't resist to expansion as much as latex/silicon/rubber bladders and it is really thin, so I can calculate its dimensions more easily.
For 20mm McKibben muscles:
- 20mm of diameter
30cm in length
0.094 liters
0.09 kg
- 72 bundles of muscles each containing 3 unactuated McKibben muscles will have in total:
20.3 liters
19.44 kg
- Contraction reduces length in 20% and increases diameter in 40%.
28mm in diameter
24cm in length
0.148 liters
0.15 kg - 72 bundle of muscles each 3 actuated McKibben Muscles will have in total:
31.9 liters
32.4 kg
- The difference is what I will have to pump in a second or less:
11.6 liters
12.96 kg - 11.6 liters per second
696 liters per minute. - I would need around 13-14 hydraulic pumps, each running at 1.25hp (4 bars of pressure).
I would need a 17hp combustion engine to run this.
- 34,8 liters per second if pumping in a third of a second.
2088 liters per minute.
- I would need 40 hydraulic pumps, each running at 1.25 hp (4 bars).
I would need a 50 hp engine to run this. - Even if I assumed that 20mm would be able to output twice the force of a 10mm McKibben muscle, I would need around 1044 liters per minute and 25hp engine.
*Actually 0.4, and I would need, in the second case, a 3.2hp engine and 8 hydraulic pumps (each costs 1300 brazilian bucks, so I don't think I will be trying this out, lol).
- Also, 20mm nylon braided sleeve costs around 7 reais (~2 dollars) per meter.
And since I would need 64,8 meters (or 43,2 meter if only 2 per bundle), it would cost more or less the same as the 10mm one.
Around 400 reais (around 75 dollars)
Around 2000 reais (383 dollars) for aramid/steel. - Now if it was 43,2 meters, it would cost 300 reais (70 dollars) for Nylon.
1300 reais (250 dollars) for Aramid/Steel.
For 50mm McKibben muscles:
Well, for this one I will only calculate for Nylon and for a single muscle per bundle, because this will definitely output more force than the 10mm one and because I can't find other braided sleeves in this size with aramid/steel. :/
- 50mm of diameter
30cm of length
0.589 liters
0.59 kg
- 72 unactuated muscles will have:
42.4 liters
42.48 kg
- Contraction reduces length in 20% and increases diameter in 40%.
70 mm of diameter.
24cm of length.
0.924 liters
0.92 kg - 72 actuated muscles would have in total:
66.5 liters
66.24 kg
- The difference is what I will have to pump in a a second or less:
24.1 liters
23.76 kg - 24.1 liters per second
1446 liters per minute. - I would need around 27 hydraulic pumps, in which each would need 1.25 hp (4 bars of pressure).
I would need a 35hp engine.
- liters per second if pumping in a third of a second.
4338 liters per minute. - I would need 83 hydraulic pumps each running at 1.25 hp.
A 104 hp engine would be required to run this thing.
*actually 33 hydraulic pumps and 13hp engine
- 50mm nylon braided sleeve costs around 20 reais (around 5 dollars) per meter, and since in this case we would need around 21 meters, it would cost around 420 reais (80 dollars).
- But since this would require an insane amount of hydraulic fluid, better not.
Now calculating a "realistically" amount of fluid flow:
I say "reallistic" because I don't really know how many muscles will actuate at "full throttle" of the suit.
- For the 10mm McKibben muscles:
36 muscles actuated in a third of a second, adding 0.022 liters per muscle, which would need 2.3 liters per second if actuated in a third of a second.
Which would be 142,56 liters per minute in total.
Around 3 hydraulic pumps each running at 1.25hp, I would need 3.75hp in total, which is 2812.5 watts per hour.
One would think that using those 3000 watts car batteries could be viable now, but each 3000 watt battery weights 50 kg, with 4 of those, the suit would weight extra 200kg, and it would only give around... 4.5 hours of run time.
If it was one third of the muscles, it would be around 24 muscles... Which would be 95,04 liters per minute, which would need 2 hydraulic pumps, which would be 2.5hp, which would consume 1800 watts per hour.
Around 6 horus of run time.
Edit¹:
While researching prices and other equipment pieces, I found out that there are hydraulic pumps on the market that can achieve around 130 liters per minute.
So... Basically, 60 liters per minute for every 1000 rpm, and since the rated rpm is 2500, I can assume it can deliver 130 liters per minute.
And since this is at merely 1.25hp of force, then, this pump would consume around 900 watts per hour, with the use of four 3000 watts car batteries, this would last around 13 hours.
Which is a nice thing, since I wouldn't need such crazy amounts of fluid.
And maybe I could force the pump a little more, since it won't be running at 200 bars or anything like that (not that I would advise you to do that).
However, the pump costs something around 1300 reais (250 dollars).
And by the way, this is 900 watts working "at full throttle", you definitly wouldn't need that much if you're just walking or carrying weight in a slow/medium speed rate, which could extend the battery's life.
And another problem that I forgot to mention in this project log is: McKibben muscles tend to under-contract under loads.
Meaning that even though the McKibben can lift 300 kgs, it won't lift the 20% distance of its length.
Which is kinda of a bummer, but also something to consider.
I also always keep out of the conversation that I will add magnetite powder so the progressive electromagnetic valves can work.
The problem is that this will significantly change the viscosity of the hydraulic fluid, and thus it will require more power to be pumped.
Meaning that maybe 1.25 hp won't be enough.
- For the 20mm McKibben muscles:
36 muscles actuated in a third of a second, adding 0.054 liters per muscle, needing 1.9 liters in a third of a second, 349,92 liters per minute in total.
Around 6-7 hydraulic pumps each running at 1.25 hp, needing 9hp.
If it was one third of the muscles, 24 muscles, 233,28 liters per minute, around 4-5 hydraulic pumps, which would need 5 hp.
- For the 50mm McKibben muscles:
36 muscles, 1/3 of a second, adding 0.335 liters, 36.18 liters per second in total, 2170,8 liters per minute in total.
Around 41 pumps, around 5hp engine to power up this crap.
Needless to say, the 10mm McKibben muscle winned this thing. >.>
Edit³:
Also, I totally forgot about something:
The lower body has to be at least 3 times stronger than the arms. :|
So, even though your arms can lift 100 kg and your legs can lift 100, you won't be able to move.
So I need to multiply the number of muscles on the legs by 3.

So, 6 bundles of muscles in the thigh, 2 in the knee, another 2 in the opposite knee and more 6 on the feet...
Which would give a total of... 96 muscles.
And I have to actuate all of those... Or else the mech/suit wouldn't move.
So... Just for the legs, if the actuated only once in during 1 second while walking (a really slow walking), 2,112 liters per second, 126 liters per minute.
If those actuated at a third of a second, then it would be 6,3 liters per second, which would give 380,16 liters per minute...
I would need 3 hydraulic pumps with 130 liters per minute, which would require 1.2 hp to run.
I thought on using pumps for water that can output more or less twice the 300 lpm value and use for hydraulic oil.
But I don't know how well it would run on oil, since oil can be 30 times more viscous than water, and these pumps are as expensive as the hydraulic ones.
Some are even made out of plastic, dunno if those would generate enough pressure and/or flow... :/
Oh yeah, I totally forgor, it is half of 96 muscles, because only half will be actuate every given time. Or else, the mech wouldn't move.
So... 190.08 liters per minute at 4 bars.
I think I can find an hydraulic pump that achieves this amount of flow.
Well, just now I found out that a human takes 100 steps per minute while walking, which would be 1.6-ish steps per second, and while jogging, 140 steps per minute, which is somethign around 2.3-ish steps per second.
Which means that a third of a second is 3 steps per second, and it is probably running at medium speeds.
Assuming that jogging is "slow" running speed.
And jogging is around 6 miles per hour (10 kph), so I will assume that medium running would be around 9-10 miles per hour (14-16 kph).
2- Calculating multi-filament McKibben muscles:
You know the drill, 10 filaments per 1kg of force. We need 300kg, so 3000 filaments each with 1mm of inner diameter, 30cm each (more or less).
So, I would need 900 meters of this thing PER MUSCLE (it is noticiable that I'm done with the subject? lol).
I would have 0.707 liters in a single bundle, 50.9 liters in total. :|
Contracted would have 1.3 liters, 99.72 liters in total.
A difference of around 50 liters, 3000 liters per minute.
Well, I'm super done with Multi-filament McKIbben muscles.
They are cool, but not for hydraulics.
Screw those. 🙄
Edit⁴:
I believe I misscalculated those, so I tried again, but if these where a single muscle each.
So... If a 30cm long 1mm thick McKibben artificial muscle where to contract, it would have 24cm in length and 1.4mm of diameter, in which only 0.236 mililiters (or 0.0002 liters) would be inside of it.
When contracted, it would have 0.369 ml inside of it (or 0.0003 liters), with a difference of 0.133 ml.
If I multiply this value by 10, which would be the number of filaments to lift 1kg, I would have to provide 1.33 ml (or 0.001 liters), now, multiplied by 300, which is the amount of kg that I need, I would only need 0,399 liters.
Now, multiplying it by 72 bundle of muscles, I would need 28 liters in total.
If those contracted in one second, this would need 1680 liters per minute.
If those contracted in a third of a second, this would need 5171,04 liters per minute.
Not as good as the previous ones, but better than what I calculated beforehand.
And to be honest, I think this one is the best one for pneumatic artificial muscles, but I couldn't find a easier way to understand how much air in liters I would need to fill those.
I can only say that I tried to calculate it using the density, mass and volume equation and I found out that I would need 2grams of air to fill this up... I think.
And to be honest, I don't really know how expensive this thing would be.
Like I said, I could just use cheap nylon and LDPE plastic, but I feel like I'm missing something that will make this extra expensive... humm 🤔
By the way, the pressure used in these muscles is so low that I think I could just use plain water to power them. :|
3- Homemade hydraulic cylinders:
First I though on a cylinder with 10cm of diameter and 30cm of travel, meaning I would need 2 liters. Needless to say, at this point if something is above 1 liter per actuator, it is not worth it. :|
Then I tried 5cm of diameter and 20cm of length, it gave 0.393 liters per actuator, but all of them at once would need around 84 liters, 15 liters if it was 36 being actuated... In a second, if it was in a third, then...
Then I thought on 32mm of diameter and 20cm of travel, the cylinder diameter said I would need 37 bars. The site says I would need 9 liters per minute.
The pipe calculator says 0.161 liters per cylinder, 12 liters in total... For 1 second.... 720 liters per minute... At around 4hp.
55hp in total, 13 pumps in total.
Also not this.
I also tested inputing values of RC hydraulic cylinders.

These have around 14mm of diameter and achieve even 30cm of stroke.
The cylinder calculator said these would need 0.012 liters, so 0.884 liters for all 72 actuators, 51 liters per minute for actuation in 1 second.
150 bars of pressure can be achieved by hydraulic pumps at around 14-15hp and 52 liters per minute.
... But, as you know, 155,52 liters per minute to actuate all in a third of a second.
If it were 36 actuators, 25,92 liters per minute to actuate all in one second, 77,76 liters per minute to actuate all in a third of a second.
So just 1 pump at 14hp.
Only problem is that every one of these cylinders cost around 150 reais (28 dollars), so... 72 of those... 10,800 reais (2000 dollars).
Yes, I could make those at home... I think... Maybe...
Maybe with carbon fiber and all that stuff...? hum... 🤔
Other options (again):
Now a random thought came to my mind and maybe shape memory alloys like Nitinol could be viable now...?
Nah, too expensive.
And the termo-actuated nylon and/or polyethylene are still not as responsive.
Also, that idea of using hundreds of micro-servo motors in a tendon driven mechsuit may be actually useful now...
Hum...🤔
I've made the calculation by the way, the micro servo would cost around 300,000 reais (57k dollars).
And the Nitinol Shape Memory Alloy (SMA) wire... Well.
In this PDF about SMA Nitinol, it shows that Nitinol wire with merely 0.5mm of diameter can lift 3 kg.
On certain websites, SMA nitinol can even be around 3mm of diameter, which, I would assume, could lift 3 times as more.
But basically, 1 wire can lift 3 kg, I need 100 of those per bundle of muscle, so 30cm average times 100, 30 meters per bundle of muscles, 72 in total, so... 2,1 kilometers of Nitinol.
Which would cost 10,000 dollars, around 50,000 reais.
On some ads on websites like Alibaba, a kg of Nitinol is around 500-700 dollars (while the website I saw before, it costs 1700 dollars per kg), so... Taking into consideration the density, mass and volume of nitinol, 2,1 kilometers of a 0.5mm nitinol wire would weight around 3kg.
Which would cost around 1500 dollars, or 7815,60 Reais.
Of course... Assuming these SMA wires are in a straight line, not twisted or spiralled. You probably could take more force out of the wires... But at higher cost, since the wires would be longer.
And besides its great initial cost... You would actually need a really small amount of power to heat and contract these muscles.
But let me remind you that these wires may or may not be fast enough to contract in less than a second, which is normally how much we move our limbs when doing things...
A third of a second, as I try and try again to obtain this enormous amount of power from the actuators, can be considered too slow for a human's movement. :/
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.