It has finally begun... *This* project, rather'n the slew of random-tangents that this project took me on.
I think it'll be a *tremendous* accomplishment if somehow I manage to fit this within 1K... As in, I think it's pretty much unlikely. But I am definitely designing with minimal-code-space in mind... (which probably serves little benefit to the end-goals, besides this contest, heh! Oh well, an interesting challenge nonetheless).
Amongst the first things... I needed a 4BYTE circular-buffer... and decided it would actually be more code-space efficient (significantly-so) to use a regular-ol' array, instead of a circular-buffer. Yeahp, that means each time I grab something from the front of the array, I have to shift the remaining elements. Still *much* smaller. And, aside from the "grab()" function, significantly faster, as well.
Also amongst the first things... I need to sum a bunch of values located in pointers. Except, in some cases those pointers won't be assigned. But you can't add *NULL and assume it'll have the value 0, so the options are to test for p==NULL, or assign a different default.
---------
Now... I'm on trying to figure out how to take an input Byte and route it appropriately. The fast-solution is a lookup-table. But we're talking 256 elements in that table, alone! That's already 1/4th of the 1KB limit!
One observation, so far: One of things I need to "look up" is a simple true/false value. It turns out, apparently, except for 3 cases (in red), the lowest-bit doesn't affect the true-ish-ness/false-ish-ness of the particular characteristic I'm looking for. Alright! So I only need a 128-element look-up-table (and a handful of if-then statements).
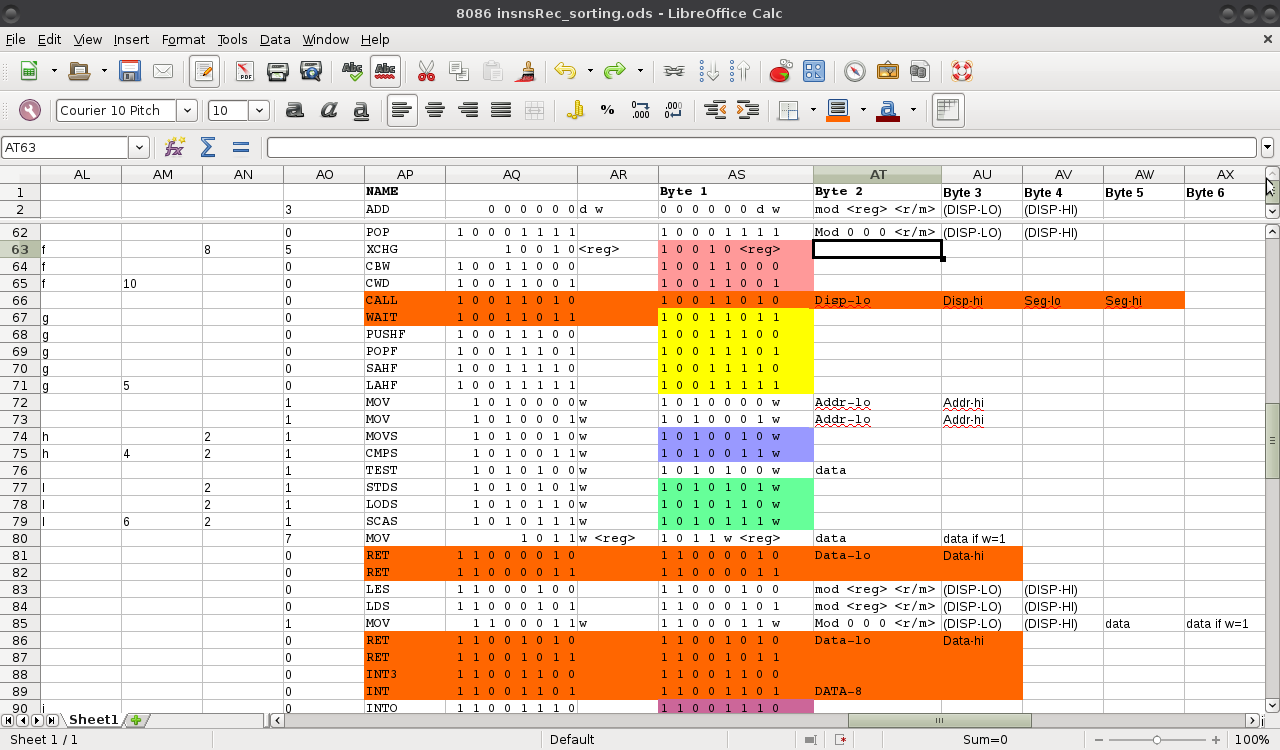
Now, better-yet... Currently I'm only looking up a True/False value. That's only a single bit. So, shouldn't I be able to divide that 128-lookup down to 128/8=16 BYTES? Now we're talking.
First idea: Simply use the first four-bits of the value to address the LUT. Then, the remaining three bits (8 values) will select one of the 8 bits in the LUT's returned byte.
Simple!
---------
The thing is, *that one* true/false value is only *one* of the *many* characteristics I'll be needing to look-up. So... The question becomes... Does this method save any space...? That has yet to be determined.
On the one hand, this particular true/false value is necessary early-on. On the other hand, if I used a 256-element LUT, I could determine *many* characteristics, simultaneously. On the other other hand, a 256-Byte LUT isn't quite enough to determine *all* the characteristics I'll be needing to determine... as, in many (but not all) cases a *second* byte is necessary.
So, the first 16-byte LUT will tell us whether a second byte is required (the true/false value I'm looking for, currently).
So, let's just pretend there was no second-byte required to determine the necessary characteristics, and the original 256-element LUT would give us all the info we'd need. I'd still need to know whether additional-bytes are necessary (in this imagining: not to determine the characteristics, but to determine *arguments*). So, somewhere in that 256-element LUT's output, I'd *still* need an indicator of whether additional bytes are necessary. Which would mean one bit in each of 256 elements (32 bytes). Which, I've already managed to reduce to 128 bits (16 bytes), and a handful of if-then statements (~10? bytes).
Now that wouldn't sound like much... I've managed to save something like 6 bytes... And, in the end, it's quite plausible the 256-element LUT will still be necessary to determine the *other* characteristics.
So, here's a reality-check... I *do* need to know whether the input requires a second byte. So, I *do* need that bit of data for each element in the 256-element LUT. But, one of the other characteristics I need to "look up" happens to have something like 130 values. Which is *just barely* too many for 7 bits. Which means I'd have to throw another bit, at the least, to the 256-element LUT to keep track of whether a second byte is required. So, now, we're talking 256 2Byte elements (HALF of the 1K limit!), rather than 256 1Byte elements. Or, even if I was able to create a 256x9bit-element LUT, I'd still be wasting 128 bits on redundant-data (seeing as how I determined that the lowest bit *seldom* affects the true/false-nature of whether a second-byte is necessary from the input).
(And, again, even 9 bits wouldn't be enough to handle all the characteristics I need to look-up... fitting this in 1K will be *quite* the challenge; improbable, if not impossible).
So... It seems to me... This path may reduce the overall LUT-code-space-usage by more than just 16 bytes (or 6?), if I continue with this logic with the other characteristics.
E.G. look again at that spreadsheet, above. Each color-grouping (besides red) indicates groupings of sequential input-values which have *very similar* characteristics. They're sparse, and for the most-part irregular. But there *are* some regularities to them, which might correspond to an input-bit-value or at least some range of input-values.
One of these sequential-groupings (not shown in the image) is actually 32 Bytes long. That means, if I use a 256-element LUT, I might be able to throw an *entirely different* LUT in that same memory-space... For instance, the 16-byte LUT I've come up with earlier, and a bit more. By throwing a few if-then statements before the 256-element look-up, I can skip those values. Now I have *only minorly-degraded* the speed-efficiency of a LUT, and can use that same space for other purposes.
(Note to drunken-self: Is a few if-then statements and a couple merged LUTs any more efficient than a couple if-then statements combined with a tiny bit of math, and separate LUTs?)
 Eric Hertz
Eric Hertz
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.