After the modification described in the previous log I let the “adjustment” and calibration procedure run again. 5 days later I repeated the calibration (without doing the adjustment). As before, all measurements are performed with an Agilent 34401A 6.5 digit multimeter.

Accuracy of the resistance

First up is a diagram that shows the absolute value of the deviation of the measurement from the setpoint. The tested values are grouped as follows:

• Calibration points: There are 55 calibration points (0 Ω, 1 Ω, 2 Ω, .., 9 Ω; 10 Ω, 20 Ω, .., 90 Ω; 100 Ω, 200 Ω, .., 900 Ω; 1 kΩ, 2 kΩ, .., 9 kΩ; 10 kΩ, 20 kΩ, .., 90 kΩ; 100 kΩ, 200 kΩ, .., 900 kΩ). In the diagram, all calibration points are connected via lines for visual purposes only. This does NOT imply that we can estimate the deviation for setpoints between two calibration points by looking at this line.
• Validation points: These are 9 randomly selected values per decade for the upper five decades. All values of the first decade are already included in the calibration points. This results in 45 additional points. Validation points are not connected by a line.

The diagram includes curves for the following scenarios:

• UNCAL@4W: The programmable resistor is used in its uncalibrated mode, where the user selectable setpoint equals the hardware setpoint. If, for example, the user enters 130 kΩ, the 6th decade would be in the 100kΩ, the 5th decade in the 30kΩ and all other decades in the shorted position. Also, the display logic ignores the calibration constants and shows 130.000 kΩ. (The input LED switches to red in order to indicate the uncalibrated mode.) For the diagram shown, the measurement was performed using a four-wire resistance measurement
• 2W: In the calibrated two-wire mode, the programmable resistor uses the two-wire calibration constants to optimize the hardware setpoint so that the actual resistance value is as close to the setpoint as possible. The calibration in this scenario is also performed using two-wire measurements
• 4W: In the calibrated four-wire mode, the programmable resistor uses the four-wire calibration constants to optimize the hardware setpoint so that the actual resistance value is as close to the setpoint as possible. The calibration in this scenario is also performed using four-wire measurements

There are two curves to assess whether/which specifications can be fulfilled:

• In order to compare the results with the requirements defined in the project description, the diagram shows a curve where the absolute value of the deviation would be equal to 0.5% of value + 0.3 Ω
• A second curve narrows the spec down to 0.1% of value + 0.15 Ω

The programmable decade resistor is not perfect. Neither is my test setup. I use an Agilent 34401A 6.5 digit multimeter for my measurements. The calibration string of the unit used for this particular calibration shows "9 NOV 2001 23.9C". I have done a plausibility check with a 1 kΩ Vishay 0.005% 2ppm/K precision resistor and it measured surprisingly close to spot on (yeah, it's only one range). Also, I have a second 34401A that shows generally very similar values, so I'm confident that the Agilent 34401A has no obvious defect. But let's be clear: That's just the best I can do right now in terms of absolute accuracy. But even if the meter had a recent successful calibration, the DMM is not perfect. Therefore the diagram includes three curves that characterize the accuracy we can expect from the Agilent 34401A multimeter (absolute value; measured values could deviate in positive as well as negative direction by the amount indicated). These are based on a Keysight datasheet ("published in USA, July 8, 2022"). With all these things out of the way, here is the diagram:

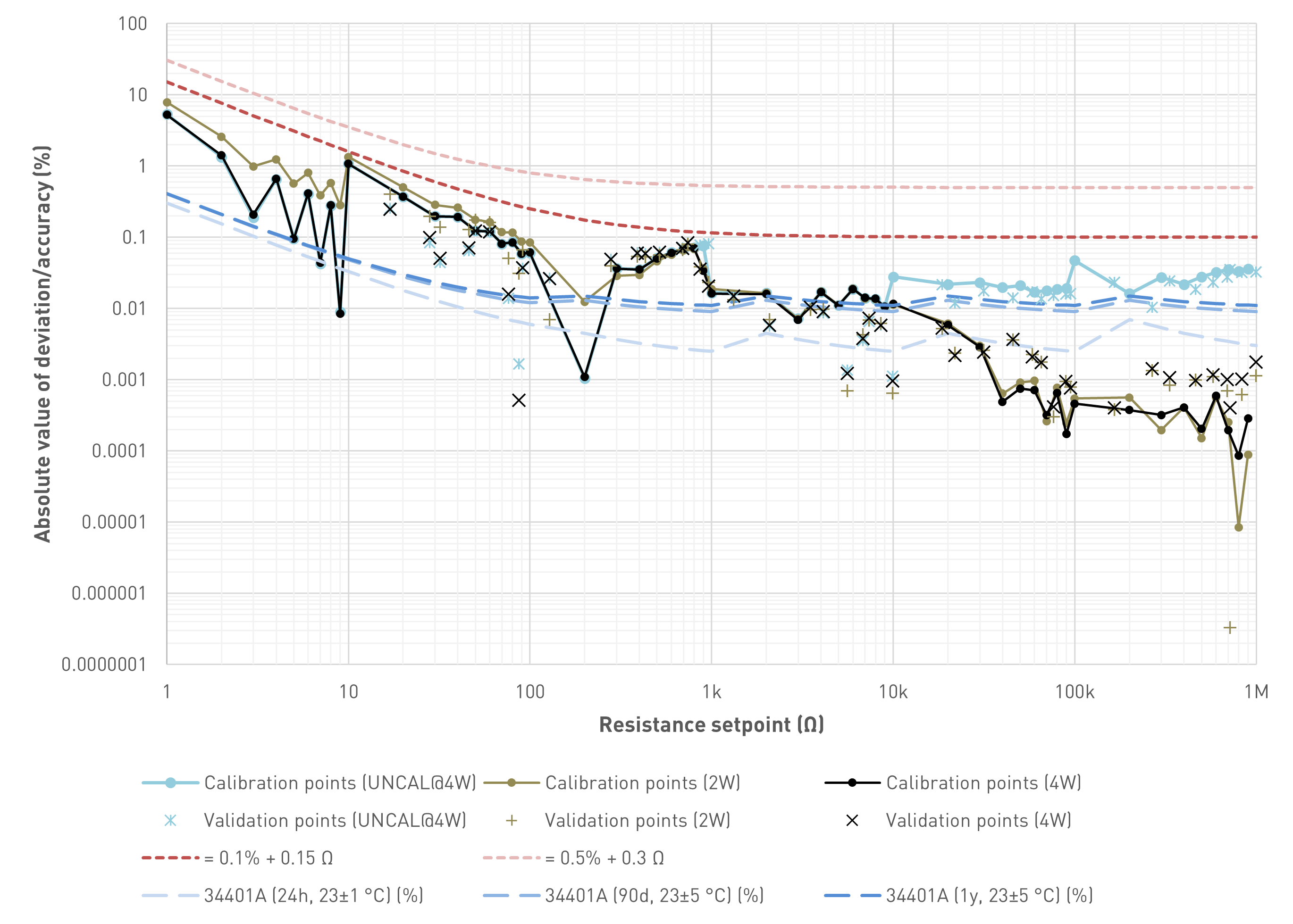
Absolute value of the deviation between the setpoint and the value indicated by the Agilent 34401A multimeter. Connecting lines between data points for visual purposes only

There are multiple observations we can make:

• With very high confidence, the absolute deviation is way below 0.5% of value + 0.3 Ω, both for four-wire as well as two-wire measurements. Hence I consider the initial goal achieved.
• The randomly selected validation points show deviations that are close to the deviations seen for calibration points close by
• The 34401A is not necessarily multiple orders of magnitude more accurate than the resistors used, especially for lower values and if not calibrated 24h beforehand. So evaluating the absolute accuracy using this setup seems to be a bit difficult
• I calibrated the programmable resistor so that it complies with the measurement results of the 34401A as good as possible. The strong improvements seen for higher setpoint values indicate that the algorithm actually does what it is supposed to do: For setpoints ≥ 50 kΩ the deviation can be reduced by an order of magnitude or thereabouts. There is no point in trying to adjust the resistance manually, the algorithm takes care of it well enough - when it's actually possible to improve something
• Assuming the 34401A measures the resistance perfectly (it doesn't as previously discussed) the deviation is below 0.1% of value + 0.15 Ω for all tested setpoints

Accuracy of the resistance

The second diagram is similar to some extent, but instead of comparing the setpoint with the actual (measured) resistance, now we compare the calculated resistance (estimate based on the calibration values) with the actual (measured) resistance. This answers the question of whether we have to measure the resistance each time we select a value, or whether it’s ok to just look at the display and trust that the value displayed is the resistance at the input.

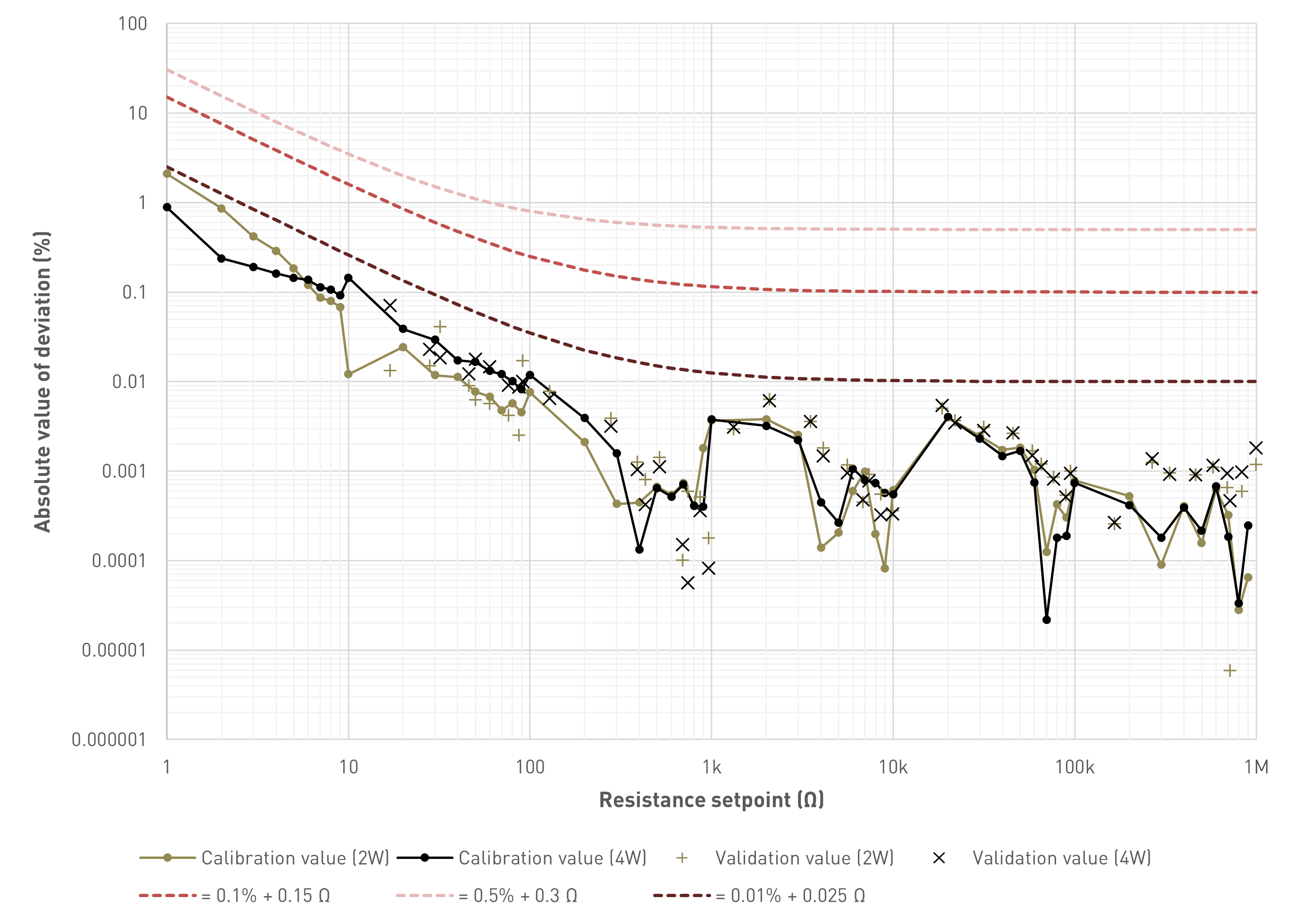
Absolute value of the deviation between the calculated resistance (estimate based on calibration values) and the value indicated by the Agilent 34401A multimeter. Connecting lines between data points for visual purposes only

Like with the accuracy, for the lowest resistance values there is some significant deviation* (worst case about 2% for two-wire and 1% for four-wire measurements at 1 Ω). However, the deviation drops really quickly. For resistance values above 10 Ω we're looking at about 0.1% (without any additive constant) deviation or less, for 100 Ω and up at a deviation of about 0.01% or less which I consider irrelevant in almost any situation this unit could be used in. In other words: In most cases the estimate is roughly one order of magnitude more accurate than the accuracy of the resistance. This leads me to the conclusion that the calculated resistance can be relied upon, with certain caveats for really low values (however, those apply for the accuracy too).

* This deviation could likely be reduced further with a software update that also stores the calibration data for the lowest decade without any compensation for the contact resistance etc. that is only required for higher decades. Shall I try it?

Automated adjustment/calibration setup using an Agilent 34401A multimeter.

Conclusion

With the fairly stable resistors used and also great calibration results I think it's fair to call it a precision instrument. Hence the label Programmable Precision Resistor on the front panel. That being said: If you're looking at an accuracy in the ppm range, things like EMF and the isolation material of the binding posts matter. Those effects were not properly considered.

Also, there are some other topics that could be very interesting like temperature and long term drift (e. g. 30 days, 90 day, 1 year). I don't have a climate chamber, but re-running the automated calibration procedure in a few months would certainly be an option. How do I know which of the instruments has drifted though? And if no change can be measured, maybe both have drifted, but in opposite directions. This gets difficult really quickly :)