To implement the VAE on a microcontroller with small SRAM and Flash footprint it is necessary to minimize the size of the network weights themselves and also consider the SRAM footprint required for evaluation.
- The size of the model in the flash is defined by the total number of parameters. I assume that it will be possible to quantize the model to 8 bit, so the model must be reduced to a few thousand of parameters to fit into the flash of a small MCU.
- The SRAM consumption is defined by the parameters that need to be stored temparily during inference. Assuming that we evaluate the net layer by layer, then we should limit the maximum memory footprint of one layer. There may also be some optimization posssible by evaluating the CNN part of the decoder tile by tile. (depth first)
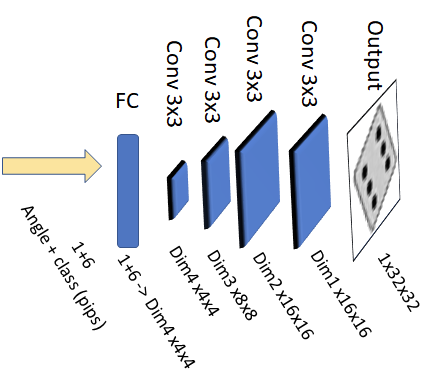
A rough sketch of the decoder model is shown above. I kept the model structure constant and changed the number of channels per layer (Dim1 to Dim4) to modify the size of the network. The last layer was intentionally chosen as an upsampling layer to recuce memory footprint during inference.
The table above shows a representative sample of test runs alogn with the results. The left part shows the channel configuration used in the model (Dim1-Dim4). The middle columns show the number of parameters in the model (CNN, fully connected layer and the sum of both). The model was trained on 8192 images for 400 epochs - overfitting does not seem to be an issue for this use case.
The rightmost columns show the evaluation results. I used two criteria:
- The LMS error of test images vs. generated images (loss).
- The fraction of correctly identified images after passing generated images through the evaluation model.
The first criterium can be seen as indicative for the visual quality of the generated image. The second criterium judges whether the number of pips of the generated die images can be deciphered. (And the evaluation model is quite good at it).
Lets have a look how these parameters relate to network size:
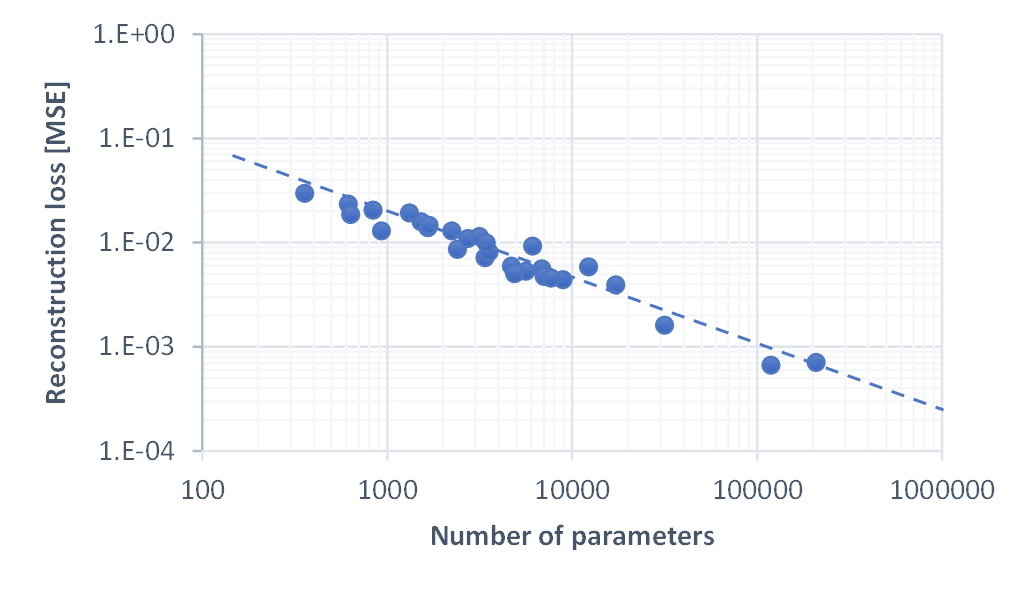
The figure above shows a log-log plot of number of parameters vs. reconstruction loss for all test runs. We can see that they roughly follow a line with a slope of -2/3, regardless of chosen network structure. This is quite fascinating and basically indicates that any added parameter improves the image quality and the image quality is inversely proportional to the number of parameters. There are diminishing returns, of course.
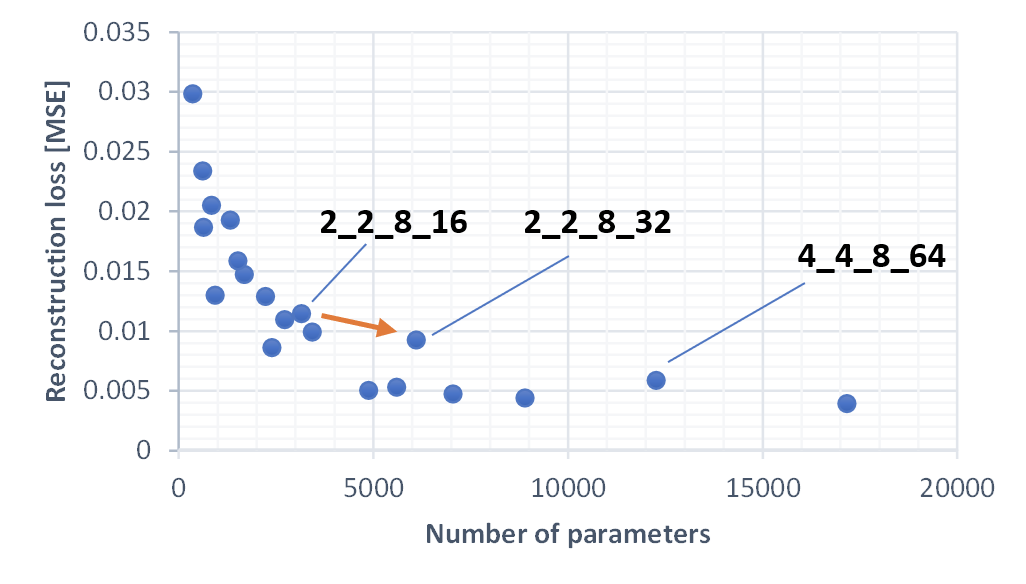
Looking closer (this is a lin-lin plot, zooming into the smaller models) we can see that there is a (weak) impact of parameter distribution. Increasing the size of dim4, which influences both the fc layer size and the number of channels in the 4x4 convolutional layer, leads to improvements that are slightly worse than the trend. In general, it appeared to be less beneficial to increase the number of channels by a large factor from one layer to another. Weights are more efficiently used, if each layer has a a similar number of channels.
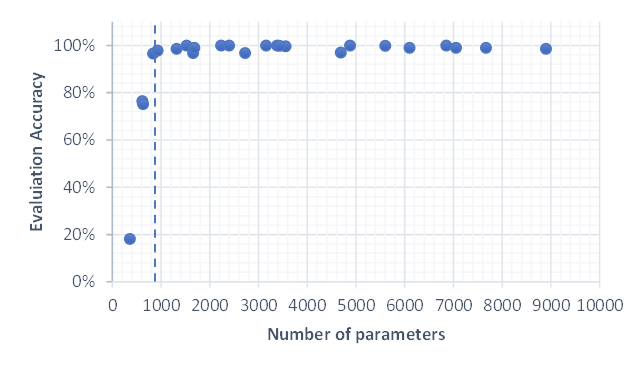
The plot above shows the accuracy for all smaller models. We can see that it is close to 100% when the number of parameters is >~900. Below it quickly reduces, meaning that no coherent images are generated anymore.
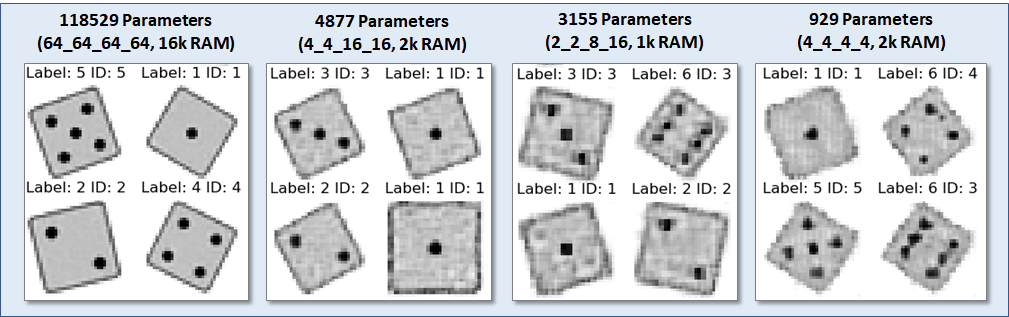 The best models for different evaluation memory footprints are shown above, along with sample images. The RAM footprint is defined by the memory requirement of the dim1x16x16 layer, assuming that two copies need to be held in SRAM.
The best models for different evaluation memory footprints are shown above, along with sample images. The RAM footprint is defined by the memory requirement of the dim1x16x16 layer, assuming that two copies need to be held in SRAM.Impressively, it is possible to generate passable die images from a model as small as 929 parameters! Considering that the size of a generated image (32x32=1024) is larger, that is quite an astonishting result,
 Tim
Tim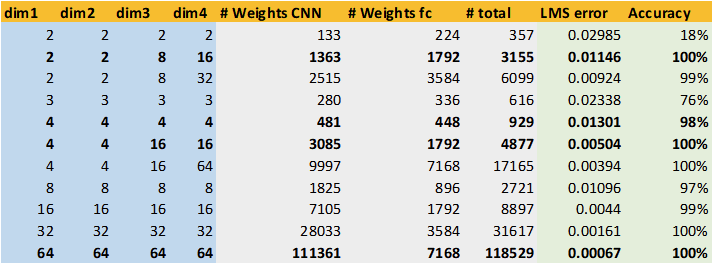
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.