Cubic Code Results
While the results are good it is not exact like the piece-wise quadratic bezier code.
I quess a fourth order bezier would bit better.
Hers is the cubic match:
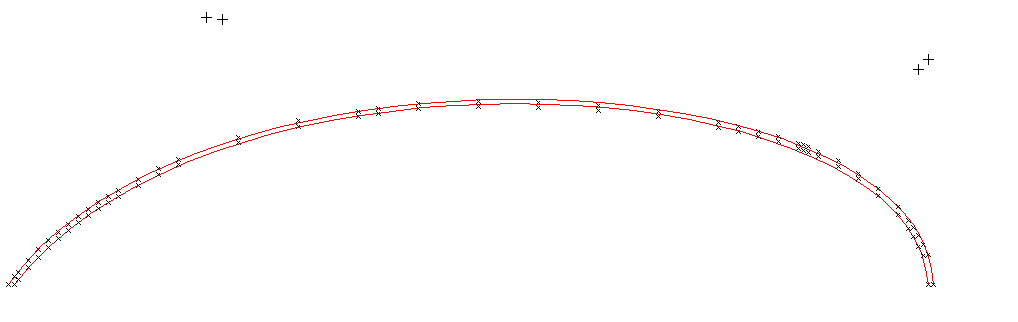
Note the bezier cuves are too wide just aft of the maxium beam and too narrow near the stern.
Here are the control points:

Here is the full code:
// Include libraries
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <string.h>
#include <math.h>
// Include in local directory:
#include "ezxdisp.h"
// Library: libezx.a
// Linker: -L. -lezx -lX11 -lm
// EZX window size
static int width=1200;
static int height=700;
static double scale=0.2;
// EZX display
static ezx_t *disp;
void PlotBezier(double Xi[],double Yi[],double Ti[],int Ni,double *Bx1,double *By1,double *Bx2,double *By2)
{
// Plot Fitted Bezier Curve
double X0,Y0,X1,Y1;
X1=Xi[0];
Y1=Yi[0];
for (int i=1;i<Ni;i++) {
double t=1.0*i/(Ni-1);
double s=(1.0-t);
X0=X1;
Y0=Y1;
X1=s*s*s*Xi[0]+3*s*s*t**Bx1+3*s*t*t**Bx2+t*t*t*Xi[Ni-1];
Y1=s*s*s*Yi[0]+3*s*s*t**By1+3*s*t*t**By2+t*t*t*Yi[Ni-1];
ezx_line_2d(disp,scale*X0,height/2-scale*Y0,scale*X1,height/2-scale*Y1,&ezx_red,1);
}
// Plot Fitted Control Point (B1)
ezx_line_2d(disp,scale**Bx1-5,height/2-scale**By1,scale**Bx1+5,height/2-scale**By1,&ezx_black,1);
ezx_line_2d(disp,scale**Bx1,height/2-scale**By1-5,scale**Bx1,height/2-scale**By1+5,&ezx_black,1);
// Plot Fitted Control Point (B2)
ezx_line_2d(disp,scale**Bx2-5,height/2-scale**By2,scale**Bx2+5,height/2-scale**By2,&ezx_black,1);
ezx_line_2d(disp,scale**Bx2,height/2-scale**By2-5,scale**Bx2,height/2-scale**By2+5,&ezx_black,1);
// Plot Input points
for (int i=0;i<Ni;i++) {
ezx_line_2d(disp,scale*Xi[i]-2,height/2-scale*Yi[i]-2,scale*Xi[i]+2,height/2-scale*Yi[i]+2,&ezx_black,1);
ezx_line_2d(disp,scale*Xi[i]+2,height/2-scale*Yi[i]-2,scale*Xi[i]-2,height/2-scale*Yi[i]+2,&ezx_black,1);
}
return;
}
void FitBezier(double Xi[],double Yi[],double Ti[],int Ni,double *x1,double *y1,double *x2,double *y2)
{
double Bx0=Xi[0];
double By0=Yi[0];
double Bx1=*x1;
double By1=*y1;
double Bx2=*x2;
double By2=*y2;
double Bx3=Xi[Ni-1];
double By3=Yi[Ni-1];
double Ex1,E1x1,E2x1;
double Ey1,E1y1,E2y1;
double Ex2,E1x2,E2x2;
double Ey2,E1y2,E2y2;
double t,e2=0.0;
do {
E1x1=0.0;
E2x1=0.0;
E1y1=0.0;
E2y1=0.0;
E1x2=0.0;
E2x2=0.0;
E1y2=0.0;
E2y2=0.0;
e2=0.0;
// Solve all t
for (int i=1;i<Ni-1;i++) {
double Et=0.0;
t=Ti[i]; // Initial t
// printf("i=%3d t=%12.6lf",i,t);
do {
double f1=(t*t*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+t*t*(3*Bx0-6*Bx1+3*Bx2)+t*(-3*Bx0+3*Bx1)+(Bx0-Xi[i]))*(6*t*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+4*t*(3*Bx0-6*Bx1+3*Bx2)+2*(-3*Bx0+3*Bx1))
+(t*t*t*(-By0+3*By1-3*By2+By3)+t*t*(3*By0-6*By1+3*By2)+t*(-3*By0+3*By1)+(By0-Yi[i]))*(6*t*t*(-By0+3*By1-3*By2+By3)+4*t*(3*By0-6*By1+3*By2)+2*(-3*By0+3*By1));
double f2=(3*t*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+2*t*(3*Bx0-6*Bx1+3*Bx2)+(-3*Bx0+3*Bx1))*(6*t*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+4*t*(3*Bx0-6*Bx1+3*Bx2)+2*(-3*Bx0+3*Bx1))
+(t*t*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+t*t*(3*Bx0-6*Bx1+3*Bx2)+t*(-3*Bx0+3*Bx1)+(Bx0-Xi[i]))*(12*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+4*(3*Bx0-6*Bx1+3*Bx2))
+(3*t*t*(-By0+3*By1-3*By2+By3)+2*t*(3*By0-6*By1+3*By2)+(-3*By0+3*By1))*(6*t*t*(-By0+3*By1-3*By2+By3)+4*t*(3*By0-6*By1+3*By2)+2*(-3*By0+3*By1))
+(t*t*t*(-By0+3*By1-3*By2+By3)+t*t*(3*By0-6*By1+3*By2)+t*(-3*By0+3*By1)+(By0-Yi[i]))*(12*t*(-By0+3*By1-3*By2+By3)+4*(3*By0-6*By1+3*By2));
Et=f1/f2;
t=t-Et;
} while (Et*Et>1e-8); // Error ~0.001
Ti[i]=t;
e2=e2+(Bx0*(1-t)*(1-t)*(1-t)+3*Bx1*(1-t)*(1-t)*t+3*Bx2*(1-t)*t*t+Bx3*t*t*t-Xi[i])*(Bx0*(1-t)*(1-t)*(1-t)+3*Bx1*(1-t)*(1-t)*t+3*Bx2*(1-t)*t*t+Bx3*t*t*t-Xi[i])
+(By0*(1-t)*(1-t)*(1-t)+3*By1*(1-t)*(1-t)*t+3*By2*(1-t)*t*t+By3*t*t*t-Yi[i])*(By0*(1-t)*(1-t)*(1-t)+3*By1*(1-t)*(1-t)*t+3*By2*(1-t)*t*t+By3*t*t*t-Yi[i]);
// printf(" -> t=%12.6lf Et*Et=%12.6lf",t,Et*Et);getchar();
// WRT: Bx1
E1x1=E1x1+6*t*(t*t*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+t*t*(3*Bx0-6*Bx1+3*Bx2)+t*(-3*Bx0+3*Bx1)+(Bx0-Xi[i]))*(t*t-2*t+1);
E2x1=E2x1+18*t*t*(t*t-2*t+1)*(t*t-2*t+1);
E1y1=E1y1+6*t*(t*t*t*(-By0+3*By1-3*By2+By3)+t*t*(3*By0-6*By1+3*By2)+t*(-3*By0+3*By1)+(By0-Yi[i]))*(t*t-2*t+1);
E2y1=E2y1+18*t*t*(t*t-2*t+1)*(t*t-2*t+1);
// WRT: Bx2
E1x2=E1x2+6*t*t*(t*t*t*(-Bx0+3*Bx1-3*Bx2+Bx3)+t*t*(3*Bx0-6*Bx1+3*Bx2)+t*(-3*Bx0+3*Bx1)+(Bx0-Xi[i]))*(1-t);
E2x2=E2x2+18*t*t*(1-t)*(1-t);
E1y2=E1y2+6*t*t*(t*t*t*(-By0+3*By1-3*By2+By3)+t*t*(3*By0-6*By1+3*By2)+t*(-3*By0+3*By1)+(By0-Yi[i]))*(1-t);
E2y2=E2y2+18*t*t*(1-t)*(1-t);
}
Ex1=E1x1/E2x1;
Ey1=E1y1/E2y1;
Bx1=Bx1-Ex1;
By1=By1-Ey1;
Ex2=E1x2/E2x2;
Ey2=E1y2/E2y2;
Bx2=Bx2-Ex2;
By2=By2-Ey2;
} while (Ex1*Ex1+Ey1*Ey1+Ex2*Ex2+Ey2*Ey2>1e-8); // Error ~0.001
*x1=Bx1;
*y1=By1;
*x2=Bx2;
*y2=By2;
// printf("e2= %15.6lf ",e2);
return;
}
int main(int argc,char **argv) {
// Unused parameters
(void)argc;
(void)argv;
// Beam (including gunwale)
const int N1=43;
double X1[]={50,83,100,150,200,250,300,350,400,450,500,550,600,700,
800,900,1200,1500,1800,1900,2100,2400,2700,3000,3300,3600,3700,
3800,3900,4000,4025,4050,4100,4200,4300,4400,4500,4550,4575,4600,
4625,4650,4675};
double Y1[]={25,64,84,144,196,241,284,325,363,397,431,463,492,547,
602,650,760,841,890,905,929,938,934,918,886,835,811,787,763,730,
721,713,690,644,580,504,413,344,310,270,223,175,25};
double* T1=(double*)calloc(N1,sizeof(double));
for (int i=0;i<N1;i++) T1[i]=1.0*i/(N1-1);
// Beam (excluding gunwale)
const int N2=41;
double X2[]={
83,100,150,200,250,300,350,400,450,500,550,600,700,800,900,1200,
1500,1800,1900,2100,2400,2700,3000,3300,3600,3700,3800,3900,4000,
4025,4050,4100,4200,4300,4400,4500,4550,4575,4600,4625,4650
};
double Y2[]={25,46,109,160,207,251,294,331,367,401,433,463,519,574,
623,733,815,864,879,904,913,909,893,861,810,786,762,737,703,695,
685,662,615,551,470,371,302,263,215,169,25};
double* T2=(double*)calloc(N2,sizeof(double));
for (int i=0;i<N2;i++) T2[i]=1.0*i/(N2-1);
disp=ezx_init(width,height,"CubicBezier Curve Fit");
ezx_set_background(disp,&ezx_white);
printf("%s\n","Gunwale:");
double Bx1=1023.147;
double By1=1349.780;
double Bx2=4651.200;
double By2=1157.687;
Bx1=(2*X1[0]+X1[N1-1])/3;
By1=(2*Y1[0]+Y1[N1-1])/3;
Bx2=(X1[0]+2*X1[N1-1])/3;
By2=(Y1[0]+2*Y1[N1-1])/3;
FitBezier(X1,Y1,T1,N1,&Bx1,&By1,&Bx2,&By2);
PlotBezier(X1,Y1,T1,N1,&Bx1,&By1,&Bx2,&By2);
printf(" X1=%12.4lf Y1=%12.4lf X2=%12.4lf Y2=%12.4lf\n",Bx1,By1,Bx2,By2);
printf("%s\n","Beam:");
Bx1=1048.996;
By1=1314.140;
Bx2=4623.123;
By2=1124.916;
Bx1=(2*X2[0]+X2[N2-1])/3;
By1=(2*Y2[0]+Y2[N2-1])/3;
Bx2=(X2[0]+2*X2[N2-1])/3;
By2=(Y2[0]+2*Y2[N2-1])/3;
FitBezier(X2,Y2,T2,N2,&Bx1,&By1,&Bx2,&By2);
PlotBezier(X2,Y2,T2,N2,&Bx1,&By1,&Bx2,&By2);
printf(" X1=%12.4lf Y1=%12.4lf X2=%12.4lf Y2=%12.4lf\n",Bx1,By1,Bx2,By2);
ezx_redraw(disp);
while (!ezx_isclosed(disp));
ezx_quit(disp);
return 0;
}
I think it is time to get back to the Lynaes 14 design.
AlanX
 agp.cooper
agp.cooper
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.