So, I have been thinking about the problem of drawing a clock face, that is, without making use of trig calls or precomputed tables, and a whole bunch of stuff comes to mind, like in the project description where I mention the fact that it is possible to construct a regular pentagon with compass and straightedge methods alone.  Yet, it is quite surprising how much actual work is involved in implementing something as simple as bisecting an arbitrary angle.  Even though, of course, once the heavy lifting is worked out in a manner worthy of Euclid, it becomes possible to have that particular tool available, with nothing more than a function call.  So, let's turn our attention, therefore, to the more general problem of drawing circles, and then to the various figures that can be inscribed therein.

You would think that adding a function call, something like draw_circle would do the trick.  But NO, there is, in fact, as far as I know, no actual draw circle function in Windows GDI.  Never has been.  Not now, and not all the way back to Windows 1.0 either.  There is a draw ellipse function that we could use if we wanted to just use GDI, but of course, I don't want to do that.  What if I wanted a simple 2D clock, or if I wanted to draw a clock face on a 3D clock tower, where the 3D hands might cast a shadow on the face of the clock, depending, of course, on the longitude and latitude, the local weather, and so on?

So, we need to be able to work with ordinary Euclidian constructions on the one hand while also being able to contemplate doing things with our planar object, like warping things onto the surface of cylinders, spheres, and so on.  Or just viewing things in 3-D, even though they might be 2-D.  Well, in any case, let's look at one way to draw a circle in 2-D and then fix it later so we can have some of the other, more fun stuff.

////////////////////////////////////////////////////////////////////
// 
//    PROPOSITION ???
//
//    Given a point on the plane representing the center of a circle
//    and a point on the plane representing a point on the
//    circumference of a circle, plot the indicated circle.
//
//    THE ELEMENTS OF EUCLID - Translated by John Casey
//    Pubished 1887 by Cambridge Press, public domain.
//
////////////////////////////////////////////////////////////////////

void euclid::draw_circle (const fpoint &p1, const fpoint &p2)
{
    SETCOLOR _(m_pdc,COLOR::yellow,NULL);

    MATH_TYPE x1,y1,x2,y2;
    MATH_TYPE dx, dy, r, r2;
    MATH_TYPE x_scale, y_scale;
    CRect rect;

    x_scale = x_dpi*m_scale;
    y_scale = y_dpi*m_scale;
    MATH_TYPE height;
    height = bounds.Height();
    
    // find radius of circle
    dx = (p1.x-p2.x);
    dy = (p1.y-p2.y);
    r = sqrt (dx*dx+dy*dy);
    x1 = (p1.x-page.x_offset)*x_scale;
    y1 = height-(p1.y-page.y_offset)*y_scale;
    r2 = r*x_scale;

    rect.bottom = y1+r2;
    rect.top = y1-r2;
    rect.right = x1+r2;
    rect.left = x1-r2;
    
//    Todo - use a custom drawing method here
//    instead of Windoze - especially when we
//    get to the point where we are going to
//    be drawing the shadow of a cone, for example
//    on another plane - in 3d of course!
    
    write (output,"euclid::draw_circle p1.x = ",p1.x,", p1.y = ",p1.y);
    write (output,", p2.x = ",p2.x,", p2.y = ",p2.y);
    writeln (output,", computed radius = ",r);

    m_pdc->Ellipse (rect);
}

 Thus, it is easy to see what is happening here.  I have a function that I am calling from another test function, and I am actually passing in the point where the angle bisectors of a test triangle intersect, as well as one of the vertexes of the indicated triangle, so as to try to draw a circle that encloses my triangle, and I think that the bounding rectangle and radius are being calculated correctly, it is just a matter of needing a better circle drawing routine, and one that uses the currently selected camera object to properly rendering drawings in the currently selected Euclidian plane.

Maybe the thing to do is implement a temporary circle-drawing routine that makes use of the just-calculated bounding rectangle, and then, even if it is easier to use trig functions and a loop, just get it done - so as to verify that bounding and inscribed circles are being calculated correctly.  Then, as a bonus, do it the way that I originally suggested so that I can also have things like "draw a random triangle, and then inscribe a regular pentagon inside the largest circle that can be inscribed inside the indicated triangle."

Yet, in any case - if I have it correctly, now that I think about it.  If you want to inscribe a circle inside a triangle, you find the point of intersection of the angle bisectors and then use any point of intersection of one of the projected lines with an opposite side as a radius to draw the desired circle.  Otherwise, to find the circle that encloses an arbitrary triangle, one needs to first bisect each side of the triangle, since each side will act as a chord of the desired circle, and therefore, if we can find the point where each of the perpendiculars to each side of the triangle intersects, then that should be the center of the outer circle, and to find the radius, we could make use of any vertex.  If I remember that correctly,

Back to Euclid.

Oh, wait!  There is just one more thing.  Not sure why I didn't include this code snippet!

....
    fpoint c_center, c_radius;
    fline bisector1 = fline(A1,J);
    fline bisector2 = fline(B1,K);
    c_center = fpoint::intersect (bisector1,bisector2);
    c_radius = L;
    m_host->draw_circle (c_center,c_radius);
....

 Alright, so I know that this code is a mess, but here is what this really does.

1. I have a class called fpoint, which I think I named it that because I was using floating point values to represent 2-D points, and I think I needed a different name than CPoint, or any other such thing that might already be defined.  An fpoint, therefore, is just a point in x,y space, using whatever math type the library is built with.
2. An fline is actually an equation of the form a*x+b*y+c=0, which defines a line in 2-D space.  Note that this is a line equation that theoretically extends to infinity, not a line that is defined as two points, which would define a line segment.
3. Thus, if earlier I found the points where the angle bisectors intersect the opposite sides of a triangle, and I named those variables J, K and L, then I can obtain the equation of one of the bisector lines by calling the constructor for an fline with the values of A1, and J, for example, as I am doing above.
4. Now we can find the point where the angle bisectors intersect, of course, by solving for two equations in two unknowns via another member function of the fpoint class.
5. Then, that is what gets passed to the draw_circle function, even though that function needs to be rewritten so that it will draw the required circle in the current "working plane".

Now, obviously, if Euclid's elements contain something like 465 proofs, demonstrations, and exercises, then an interesting question must arise, like I said earlier, about the construction of the pentagon, or the hour and minute marks of the clock face, etc.,, or else doing AI related stuff, like generating proofs, maybe?

Obviously, not quite to the point where I can copy and paste proofs out of Euclid into Eliza, let's say - and generate drawings, but that part does seem doable.  Finding and checking proofs, on the other hand, I am not sure just how hard that actually is.  Maybe not so hard after all?

So, of course, I am thinking about how one would go about creating an AI from scratch, where you could type in a request such as "draw a random triangle and then inscribe a regular pentagon inside the largest circle that can be inscribed inside the indicated triangle", as suggested earlier.  If the problem has already been solved, then even Eliza could be hacked up to appear to "know" how to do it.  The problem with AI, as always, is being able to solve problems that it has never seen before.

Maybe I will see if Deep Seek is up to the task.  I just realized that, just as it says in Euclid, you are supposed to find the lines perpendicular to the sides that pass through the point where the bisectors intersect, and that is how one gets the radius of the inner circle.  Well, maybe.  Better check Euclid again and then go back and edit the code!

Aarrrgh!  Looking at my code, I think that I have the correct function that I should have used, and one more good reason for NOT putting euclid.cpp up on Git just quite yet.

////////////////////////////////////////////////////////////////////
//
//    "PROP. XI.—Problem. From a given point (C) in
//    a given right line (AB) to draw a right line 
//    perpendicular to the given line. (Book 1: page 16)"
//
//      "PROP. XII.—Problem. To draw a perpendicular to a given 
//    indefinite right line (AB) from a given point (C)
//    without it.  (Book 1: page 17)"
//
//    THE ELEMENTS OF EUCLID - Translated by John Casey
//    Pubished 1887 by Cambridge Press, public domain.
//
////////////////////////////////////////////////////////////////////

fline fline::perpendicular (const fline &L, const fpoint &pt)
{
// a perpendicular line can be found if we simply
// rotate the original line by 90 degrees, and
// then solve for c based on our given point
// like we did for parallels.

    fline result;
    result.a = -L.b;
    result.b = L.a;
    result.c = -(result.a*pt.x+result.b*pt.y);
    return result;
}

 Weird how simple that should be. Thus, now I need to go back and rewrite my previous code blunder.  In the meantime, if you ask GPT if you have 12 eggs, break two, scramble two, cook two, and eat two, well, how many eggs do you have left?  I don't know if they have fixed that one yet, either.

Well, in any case, here is the corrected code snippet, this time - I think - which makes use of the already calculated angle bisectors from the earlier example.

...
    fpoint c_center, c_radius;
    fline bisector1 = fline(A1,J);
    fline bisector2 = fline(B1,K);
    c_center = fpoint::intersect (bisector1,bisector2);
    fline radial = fline::perpendicular (AB,c_center);
    c_radius = fpoint::intersect (AB,radial);
    m_host->draw_circle (c_center,c_radius);
...

 The difference is very subtle, of course.  Yet, the answer is right there in Euclid.  Yet, this seems to imply something, like maybe if it takes something like 50,000 lines of code to implement a functional game engine, just to get things going - on the one hand.  At the same time, what if every proof in Euclid could be reduced to just a dozen lines of code, or so.  Generating arbitrary proofs for problems that have never been seen before is, of course, another matter.

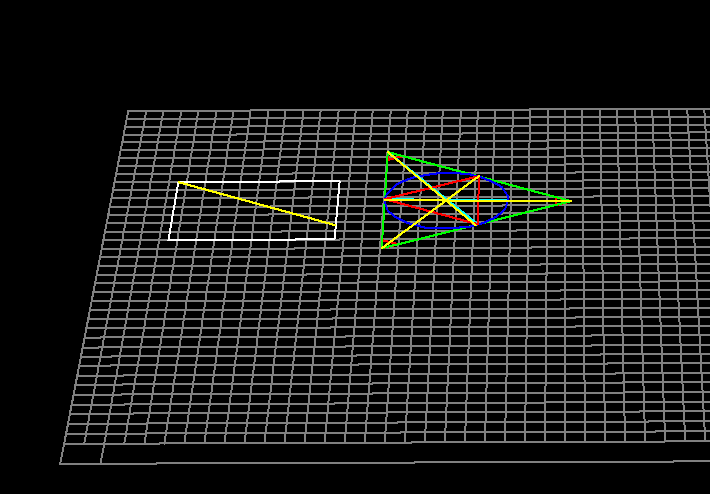
In the meantime, pun intended, of course, I did some fix-up on some code from my Tiny-CAD project from a while back, and as far as that goes, things are moving along nicely, as I work on more of the pieces, not just for drawing a clock, but for doing a whole bunch more fun stuff that involves anything and everything else that might be possible in the realm of Euclidian constructions.  Yet I must say that it should seem obvious that if I do end up at least rendering all of the graphics from Euclid's Elements, since maybe it isn't all that hard to do, then maybe there is a use case for transformers, LLMs, and so on, where maybe I could try training an AI on the text of Euclid, and well, see what happens if we give the infinite number of monkeys a proof-generating engine.