Alright, I got the code for drawing a decagon working by using the points of a pentagon to get things started,

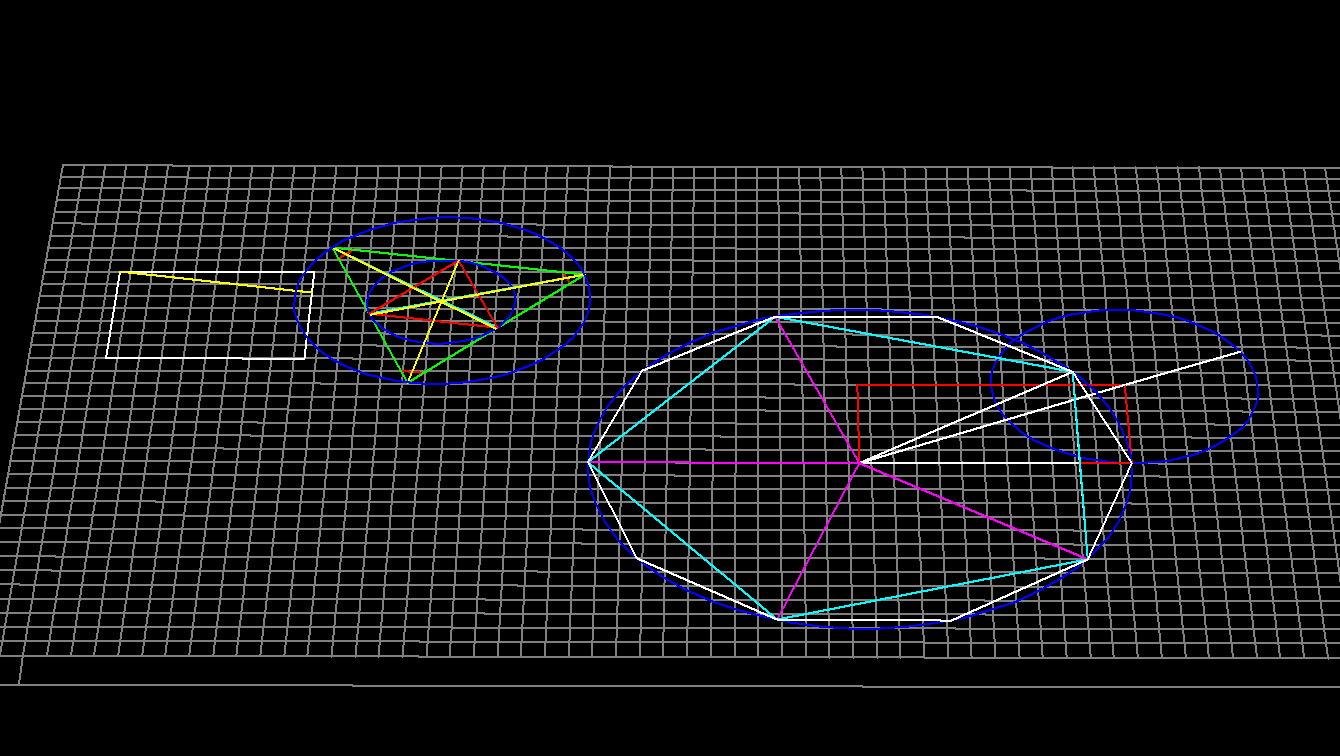
There are at least three ways that I can think of for doing this.  One would of course be to compute the angle bisectors of the internal triangles, which would be computationally expensive, but it would also be useful to take a look at some law of cosines computed values for the various internal angles, just as a test to see how much round-off error is being accumulated.  All without making use of trig calls, of course!  Then there is the method of simply finding the midpoint of each edge and plotting additional vertices by extending a line from the center of the pentagon to the point where it would intersect a circle.  A third method might be to simply reflect the set of vertices of the pentagon by any suitable axis of asymmetry.

Otherwise, I haven't decided just how far I want to go with the branchless programming meme, but it does appear to have a lot of life left in it, if I decide to push things further.  Another potentially useful variation would be to use so-called "trampolines" to help in the translation, let's say, of some kind of Eliza-style command parser that takes English text in the form of statements like "Determine the bisectors of angle ABC, and plot the points as D, E, and F.  Thus, lookup tables for words like "bisectors" might be used to map English text onto the addresses of callable functions.  Maybe then a simple AI could more or less "read" Euclid's elements directly, and create the appropriate drawings without needing to write additional code?

This would save a considerable amount of time.