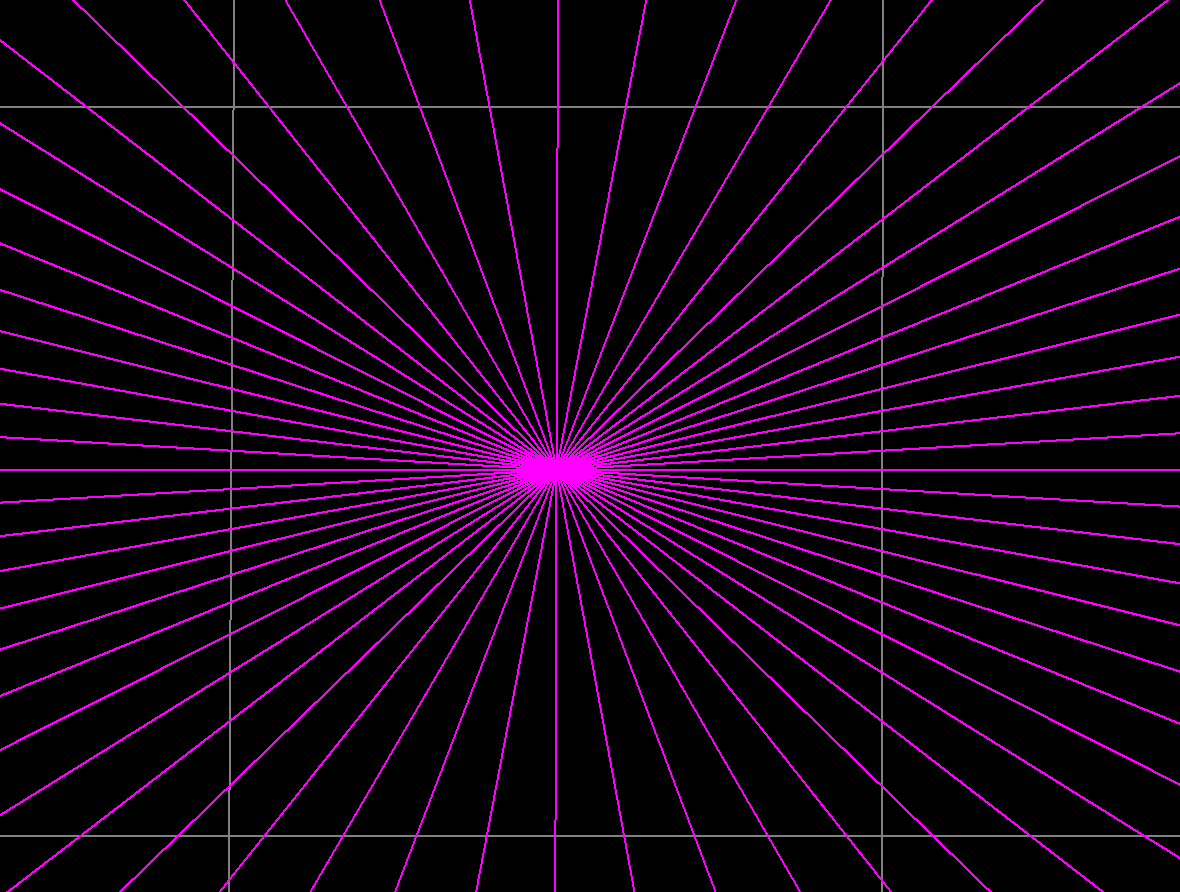
First attempt at doing a test rendering of the "calculation" for the minute marks with this code.  Ran "correctly" on the first try. Zooming out will show what is really happening.

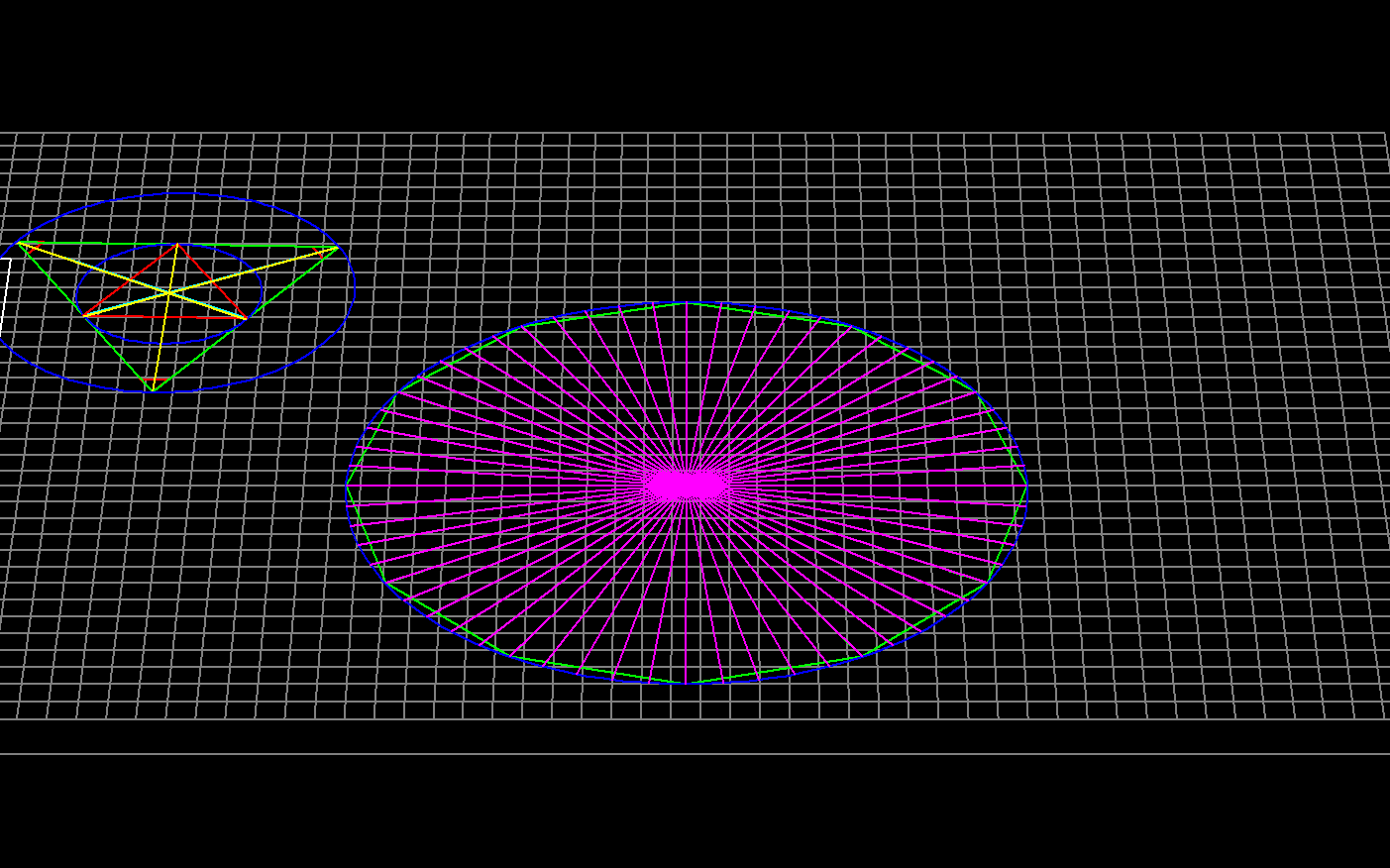
With this code no less:

void euclidian::draw_clock ()
{
    vector<fpoint> hrot;
    fpoint minute_marks [60];
    dodecagon hour_marks;
    pentagon penta;

    hour_marks = construct_dodecagon (false);
    penta = construct_pentagon (false);
    euclidian::bind(*m_host,hour_marks);
    hour_marks.on_draw (true,true);
    fpoint center = hour_marks.m_center;
    fpoint radial = hour_marks.m_points[0];
    m_host->draw_polygon(center,radial);

    int i,j;
    angle a;
    hrot.resize (12);
    for (i=0;i<5;i++) {
        a = angle(fline(penta.m_points[i],penta.m_center));
        for (j=0;j<12;j++)
        hrot[j] = hour_marks.m_points [j];
        a.angle::rotate_points (hrot,hour_marks.m_center);
        for (j=0;j<12;j++)
        minute_marks[12*i+j]=hrot[j];
    }
    SETCOLOR _(m_host->m_pdc,COLOR::magenta);
    for (i=0;i<60;i++)
    {
        m_host->draw_line (hour_marks.m_center,minute_marks[i]);
    }
}

Well, there is still a bit of work to do.  Like I might want to consider running quick sort on the minute marks, because they are most likely written to the vector of fpoints in a somewhat scrambled or shuffled fashion.  Even though now that I am thinking about it, that wouldn't be necessary if all that we are doing is using the point cloud to decide where to draw the actual and therefore properly determined minute marks, which should therefore be possible to draw, now, that is, in another piece of code. Hopefully, let's say, after a whole lot of this stuff gets refactored and then moved to a constructor.

Or maybe I can actually run quicksort on the array, using a custom comparison function that compares the angles of adjacent points.  Something that is certainly worth looking into, even if that involves using trig functions, just to see what is really happening here.  Of course, if you didn't know that Gauss, I think, was the one who figured out how to do a 17-sided rigorous construction, and of course, 3 times 5 times 17 is 255, which means that a regular 255-sided polygon is also a theoretical compass and straight edge construction, which will have to wait for another time. 

A quick screenshot of some debugging information, where I call a function to calculate the actual angle of each line, as it is being drawn, shows what is happening.

The good news is that it is exactly what I was expecting!  That being the nature of the design, code, compile, test, debug, etc., cycle.  Wanting to see results.  Now!  And getting an interesting, fun surprise now and then.  Now, like I said, I am thinking that I can still calculate the locations for my minute marks with this stuff.  Not a problem there.  Yet, I must confess that I have some circle drawing code that elsewhere is actually pre-calculating the points of a polygon with a "large number of sides" by actually making some calls to sine and cosine.  And THAT code needs to GO, since what I want to try instead is some kind of quadratic interpolation based on sets of three or four points, depending on the required resolution, and so on, and that will require that the points be sorted.  What to do, therefore?  Quicksort the array, or figure out how to fix the issue with modular arithmetic as the array is being created?  Hmm?  What would Eratosthenes or Pythagoras do?  Or Ptolemy, for that matter?

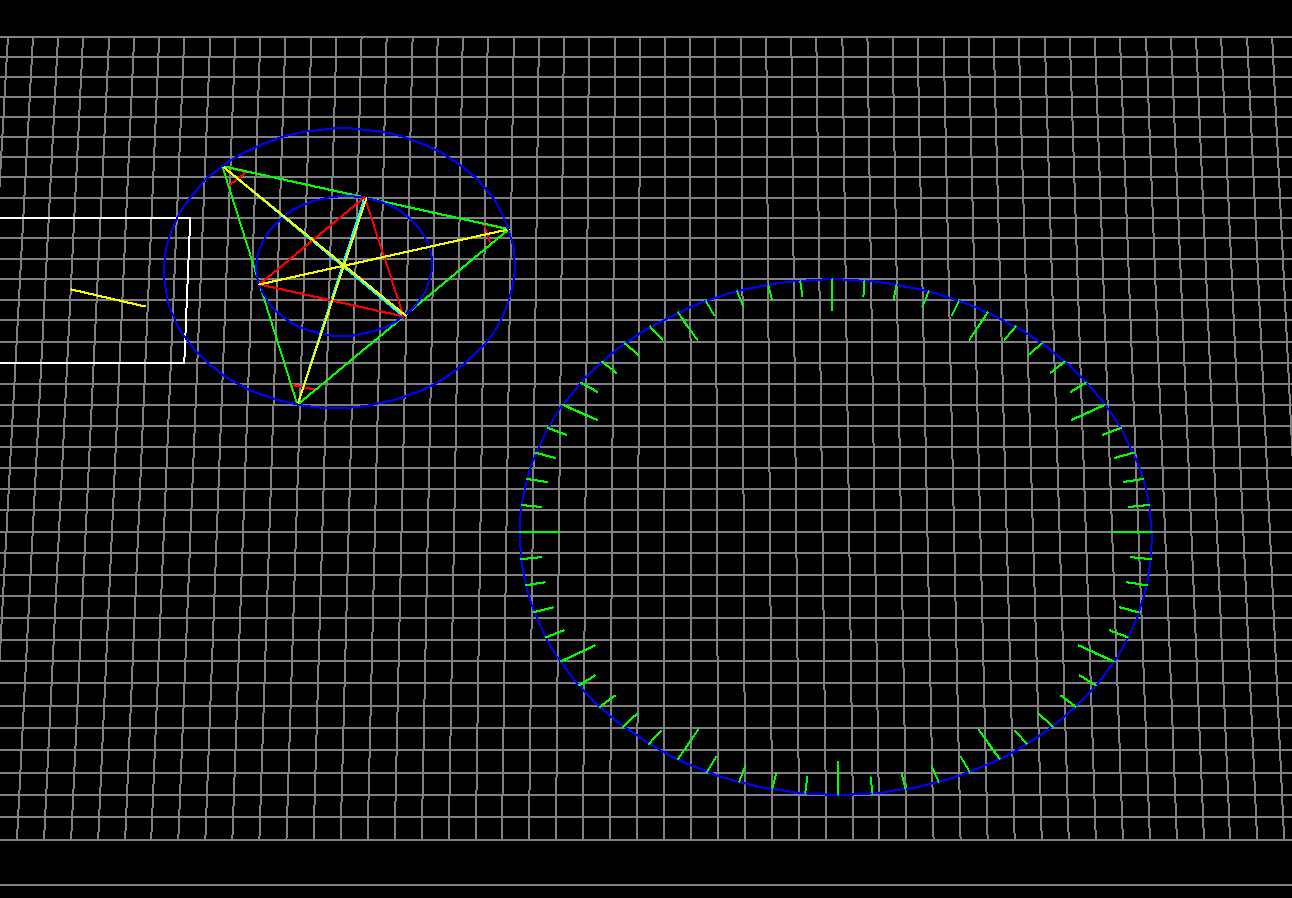
Well, anyway.  A little more tweaking with the drawing code, and it is starting to look like something.  Even if the array that holds the coordinates for the minute marks is still unsorted.  Then it occurred to me, that in order to actually draw the time, without using trigonometric functions, I am going to need to be able to do a table lookup of the relevant locations, so that I can use a hopefully faster method, like simple linear interpolation, or quadratic interpolation, as I also suggested, to find the exact points to play connect the lines with.  Then maybe work on some OpenGL stuff