Up to this point we've done everything we would need to build a true, accurate, metronome. It's time to break out the maths and build a model for our metronalmost that can be proved to never return Hackaday's target 1 Hz tick rate.
A normal, or Gaussian, distribution can be used to build a mean-weighted random number generator. Numbers will be clustered around the middle and only rarely appear towards the edges of the range.
If we take a notch out of the middle, the distribution will not generate numbers within that smaller range.
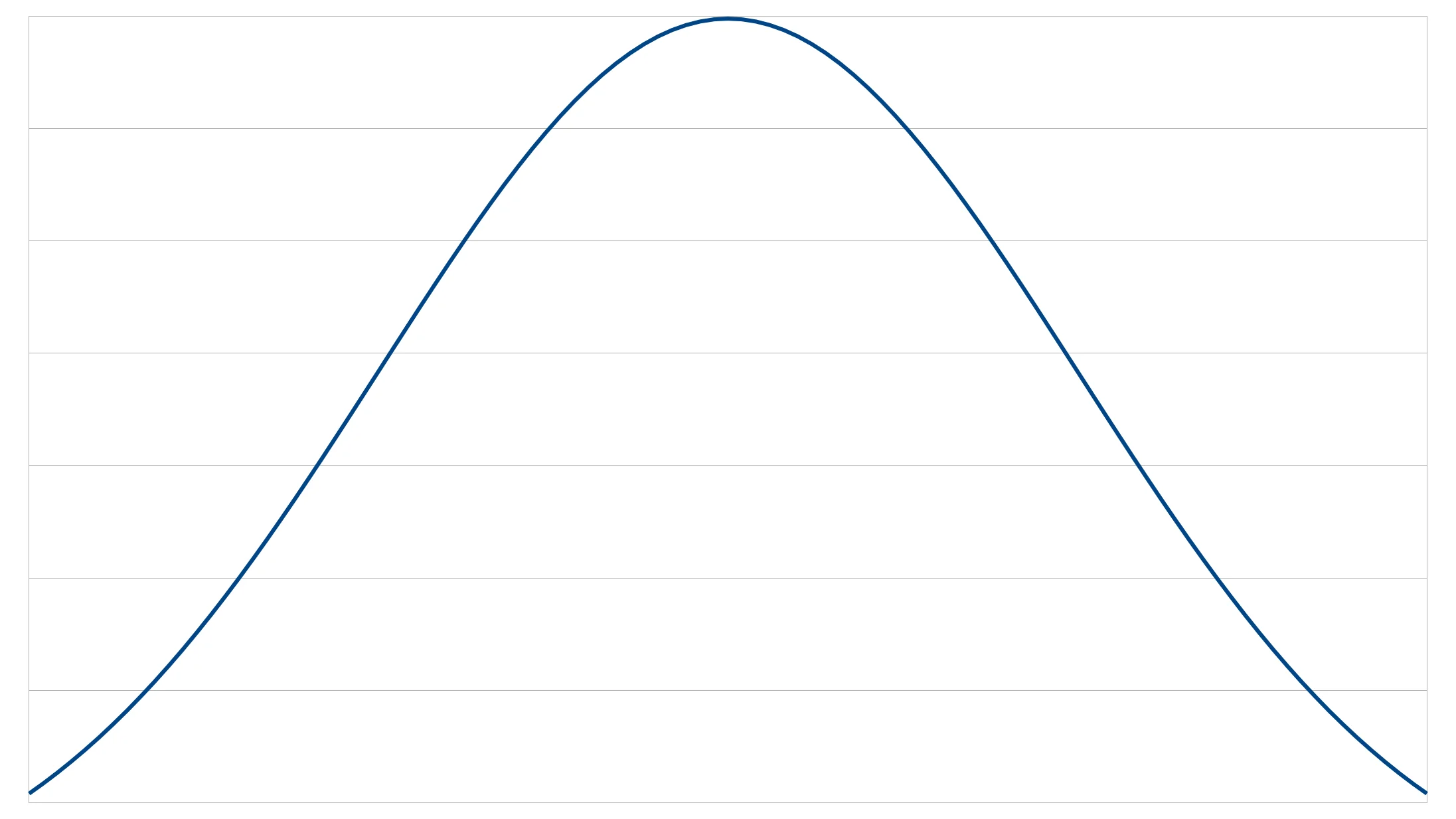 | 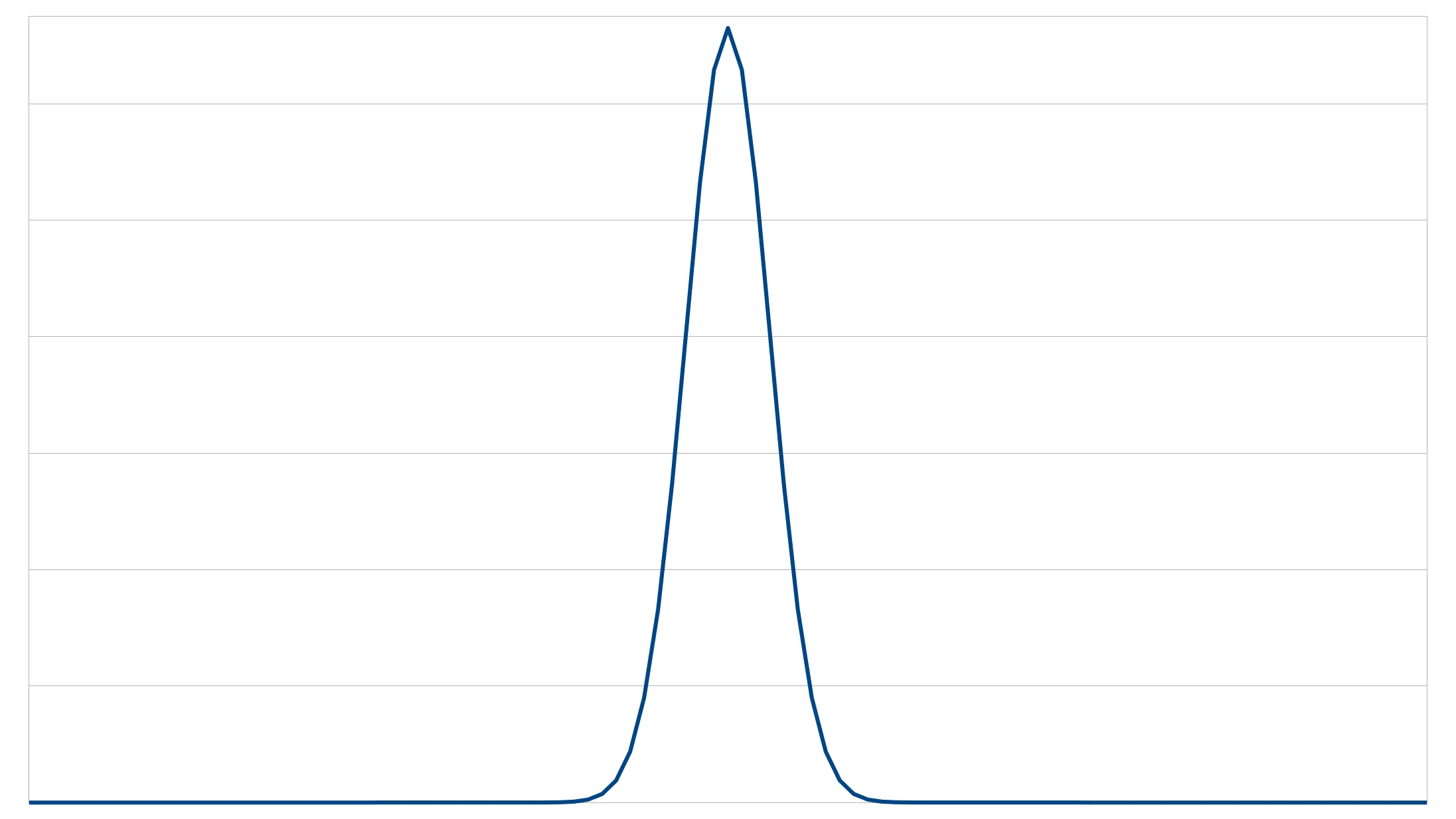 | 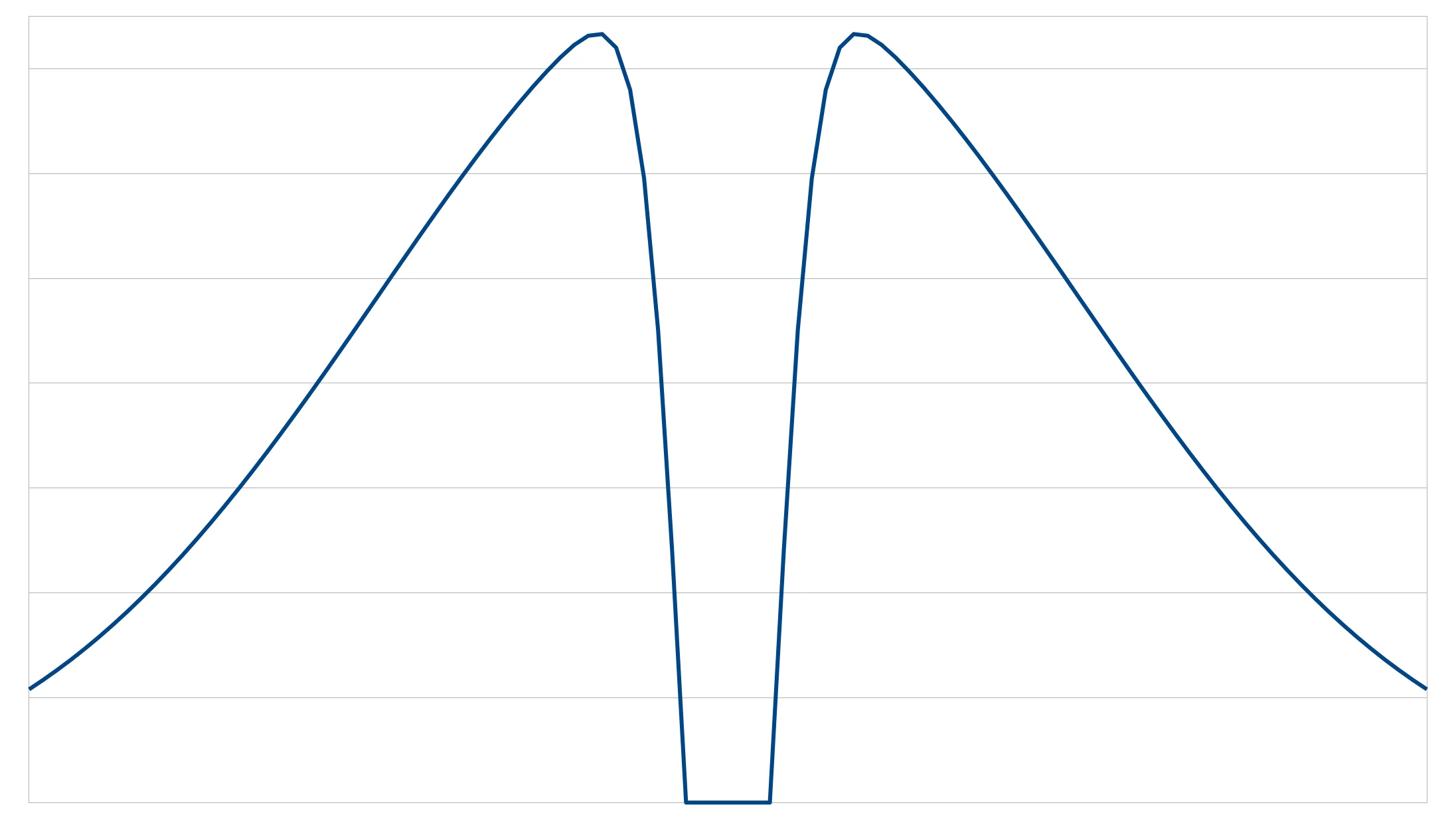 |
If we look at this notched-out function's cumulative distribution function instead of its probability distribution function, we can see a flat spot over the notch. This means that numbers are not being generated within this flattened range. Transposing the axes allows us to turn this in to a mapping function that turns a uniform random number (0.0–1.0) in to a centrally weighted, but stepped, number generator.
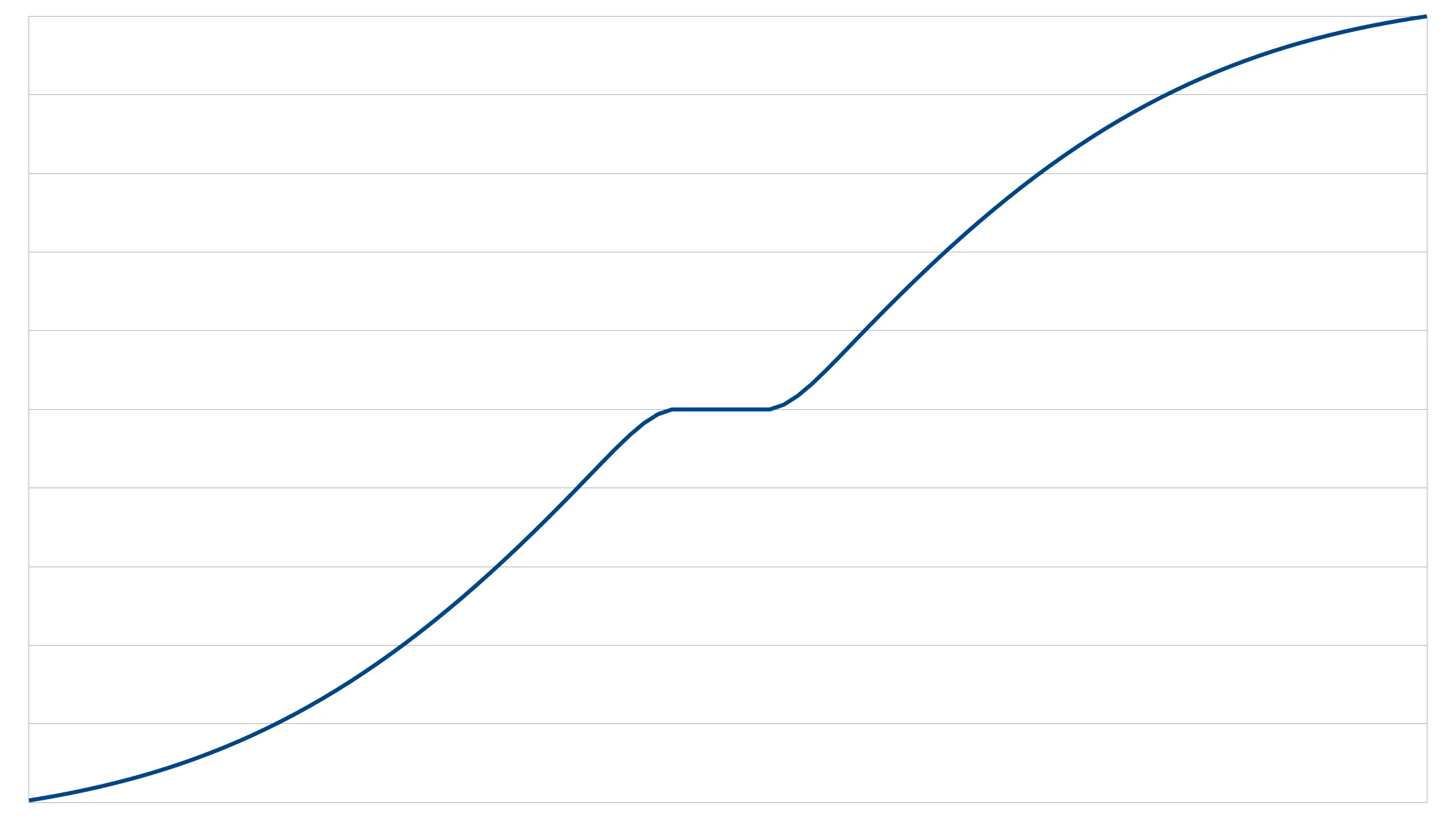 | 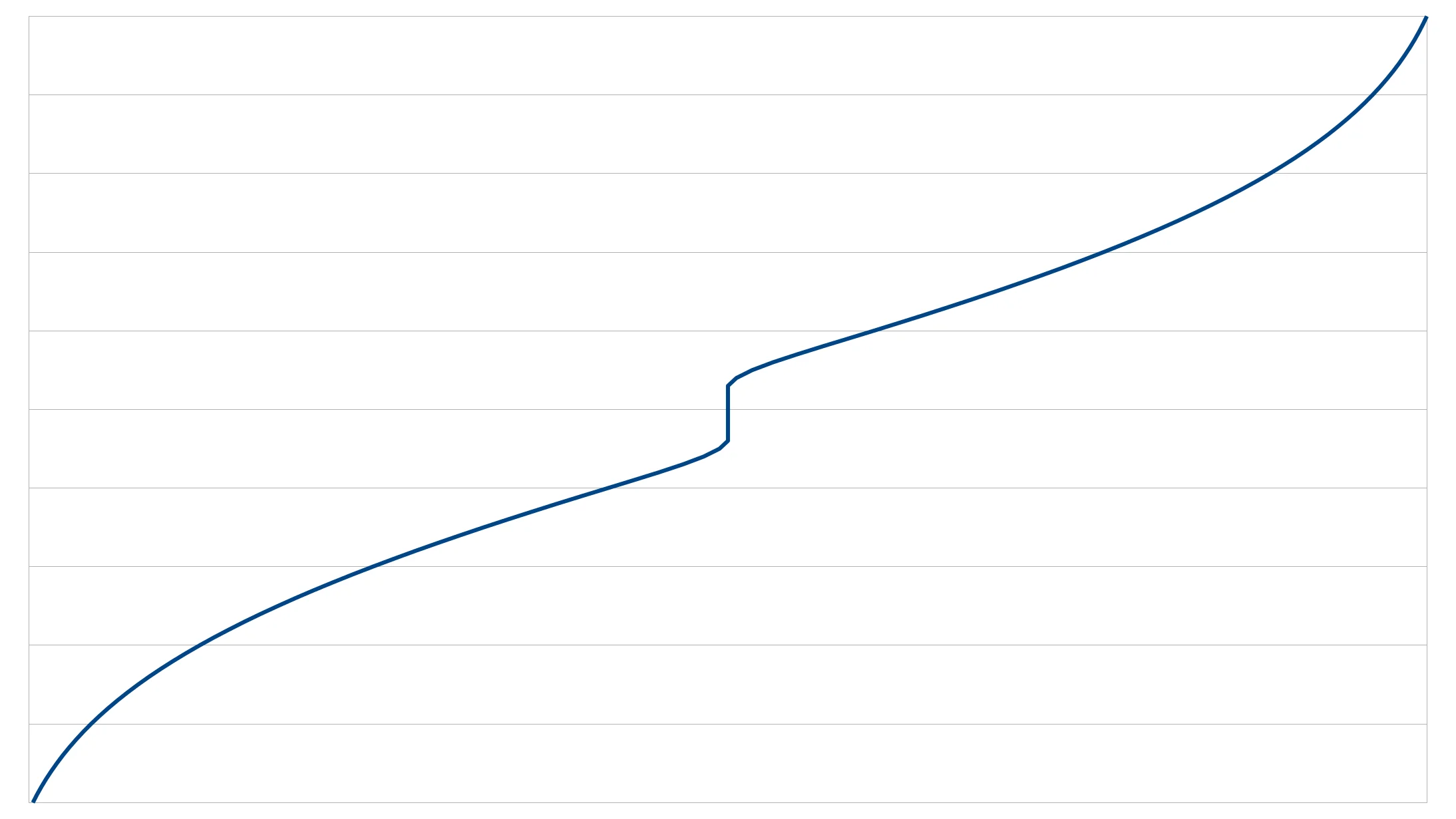 |
This new number mapping function maps 0.0 to 0.0 and 1.0 to 1.0 as normal, but maps 0.49 to 0.45 and 0.50 to 0.54. The discontinuity means a value of 0.5 can never be generated. Applying this mapping over a period of between 0.5 and 1.5 seconds will give us our almost, but never quite, 1 Hz metronome.
 Mike Coats
Mike Coats
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.