If we try to summarize what we have seen so far:
- Arithmetic operations on arbitrary analog values are better performed using digital numbers to get a repeatable accuracy
- Unsigned integer digital numbers are represented as base 2 (binary) numbers using only 0 and 1 values, using a positional notation with enough binary digits (bits). Using only 2 values offers the simplest and most effective design to store digital numbers in a physical device
- Signed integer digital numbers are represented using a 2's complement notation but otherwise follow the same arithmetic rules as unsigned integer digital numbers
- Non-integer numbers can be represented using:
- a fixed-point notation where the decimal point position is implicit and a given number of bits right of it are used to hold the fractional part of the number, following the same arithmetic rules as integer digital numbers
- a floating point notation where the decimal point position is given by an integer exponent, and the remaining bits hold the fractional part of the number as the mantissa. Both the exponent and mantissa parts still follow the same arithmetic rules as integer digital numbers
- Arithmetic operations on digital numbers can be reduced to subtraction operations
- Subtraction operation can be implemented using the basic logic operations from the Boolean algebra, although adding the addition operation does not cost much, and having positional shift or rotation operations helps implementing multiplication and division operations more efficiently, which would otherwise require complex specific hardware
- Simple as well as bitwise (i.e., performed on a set of bits that can be used equivalently to store a digital number) logic conditions can of course be implemented using the same basic logic operations from the Boolean algebra
Thus, digital computers can perform all arithmetic and logic operations only using Boolean algebra values, operations and laws, which will be described below in details, using simple undergraduate maths.
It is thus a formalism for describing logical relations in the same way that ordinary algebra describes numeric relations.
Values
Unlike elementary algebra which deals with an infinite set of numbers, Boolean algebra is using a finite set of only 2 elements. These 2 values can be indifferently called true and false, T and F, 0 and 1, or any other couple of symbols, but they are generally represented with the bits (binary digits) 0 and 1, as the XOR (exclusive-or) and AND (conjunction) operations (see below) plays the role of the addition (+) and multiplication (x) operations in integer arithmetic modulo 2, for which 1 + 1 = 0, but unlike common arithmetic, where 1 + 1 = 2. The OR operation (inclusive-or or disjunction) is then defined as x + y + xy.
Manipulating only 2 values is very nice, since it enables using the method of proof of perfect induction or proof by exhaustion, i.e., the verification for all possible cases for demonstrating theorems, as the number of cases is very small.
Operations
Boolean operations are functions having zero or more Boolean input values (in the set {0, 1}) to a single Boolean output value.
The number of operands is the arity of the operation. An operation of arity zero, or 0-ary operation is a constant, and the Boolean algebra only deals with unary operations (with arity 1) and binary operations (with arity 2).
Unary Operations
If we consider all possible calculations from 1 binary input value p to an output value, there are only 2 ^ 2 = 4 unary operations:

| Operation | Name | Symbol | Value |
|---|---|---|---|
| FALSE | Logicalfalse | ⊥, Op | The output value is always false, regardless of the input value of p. |
| IDENT | Logical identity | p | Logical identity is an operation on one input value p, for which the output value remains p. |
| NOT | Logical negation | ¬p, ~p, Np, Fp | Logical negation is an operation on one logical value p, or which the output value is true if its input value is false and its value is false if its input value is true. |
| TRUE | Logical true | ⊤, Vp | The output value is always true, regardless of the input value of p. |
Binary Operations
For calculations from 2 binary inputs p and q to an output values, each inputs with two possible values, there are 2 ^ 2 = 4 possible combinations of inputs. Because each output can have two possible values, there are 2 ^ 4 = 16 possible binary operations:
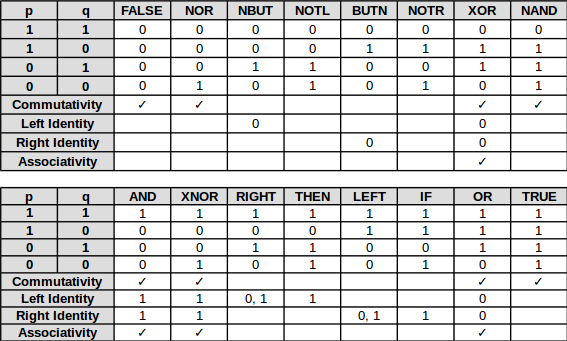
- Commutativity means that the operation follows the identity p OP q = q OP p holds, i.e., for p ≠ q (for the lines in the table above where p = 0 and q = 1 or p = 1 and q = 0), the result is the same.
- Left identity, when present, provides the value(s) p on the left side of the operator that leaves the value on the right side of the operator unchanged.
- Right identity is the same on the other side of the operator with value(s) of q.
- Associativity means that for 3 binary values a, b and c, the identity (a OP b) OP c = a OP (b OP c) holds. This is equivalent to say that the operator has both left and right identity and it is the same value.
Here are enumerated all possible operations, and their equivalent representations:
| Operation | Name | Symbol | Value |
|---|---|---|---|
| FALSE | Contradiction | false, ⊥, Opq | The output value is always false, regardless of the input values of p and q. |
| NOR | Logical negation of logical disjunction, Peirce's arrow, Quine's dagger, ampheck, neither-nor | p ↓ q, Xpq | The output value of true if both of input values p and q are false. In other words, it produces a value of false if at least one of its input values is true. |
| NBUT | Converse nonimplication | p ↚ q, Mpq | The output value is true if p is false (NOT p) BUT q is true. |
| NOTL | Left negation | ¬p, ~p, Np, Fpq | The output value is true if the LEFT input value p is NOT true. |
| BUTN | Material nonimplication | p ↛ q, p ⊅ q, Lpq | The output value is true if p is true BUT q is false (NOT q). |
| NOTR | Right negation | ¬q, ~q, Nq, Gpq | The output value is true if the RIGHT input value q is NOT true. |
| XOR | Exclusive disjunction | p ⊕ q, p ⊻ q, p ↮ q, p ≢ q, Jpq | The output value is true whenever the inputs values differ. |
| NAND | Logical negation of logical conjunction, Sheffer stroke | p ↑ q, p | q, Dpq | The output value is true, if and only if, at least one of the input value is false. |
| AND | Logical conjunction | p ∧ q, p ᛫ q, p * q, pq, Kpq | The output value is true if both of input values are true. |
| XNOR | Logical equality, logical biconditional | p ↔q, p ≡ q, p = q, Epq | The output value is true if and only if both input values are false or both input values are true. |
| RIGHT | Projection function | q, Hpq | The output value is the same as the right input value q. |
| THEN | Material implication, material conditional | p → q, p ⊃ q, p ⇒ q, Cpq | If p is true, THEN the output value is the same as the input value q and true otherwise. |
| LEFT | Projection function | p ,Ipq | The output value is the same as the left input value p. |
| IF | Converse implication | p ← q, p ⊂ q, Bpq | The output value is the same as input value p IF the input value q is true and true otherwise. |
| OR | Logical disjunction | p ∨ q, p + q, Apq | The output value is true if at least one of input values is true. |
| TRUE | Tautology | true, ⊤, Vpq | The output value is always true, regardless of the input values of p and q. |
Basis
The operations need not be all explicitly stated. A basis is any set from which the remaining operations can be obtained by composition. A Boolean algebra may be defined from any of several different bases. There are three bases for Boolean algebra that are in common use:
- The lattice basis containing the [AND, OR, NOT] operations mostly used for logical processes. Most treatments of Boolean algebra assume the lattice basis
- The ring basis containing the [AND, XOR] operations mostly used for abstract algebra considerations
- Since all operations can be defined in terms of the Sheffer stroke [NAND] (or its dual [NOR]) operations, the resulting single-operation basis has become the basis of choice for analyzing digital circuits, as all circuits can be turned into a combination of NAND (or NOR) operations
Laws
If we assume the lattice basis, the Boolean algebra satisfies a set of identities between two Boolean terms, where a Boolean term is defined as an expression built up from variables, the underlying set of constants 0 and 1 and using the 3 basic operations ( [AND, OR, NOT]) . These identities are called laws, which can conveniently be proven using the method of proof of perfect induction, given the small number of cases.
Monotone Axioms
If we use the symbols commonly used for analyzing digital circuits (‧ or implicit for AND, + for OR and ~ for NOT), the following axioms hold:
| (a) | (b) | ||
| x + 0 = x | x ‧ 1 = x | identity | (II) |
| x + y = y + x | xy = yx | commutativity | (III) |
| x + yz = (x + y) (x + z) | x(y + z) = xy + xz | distributivity | (IV) |
All of the laws above use only AND and OR operations. These operations have the property that changing either argument either leaves the output unchanged or the output changes in the same way as the input. Equivalently, changing any variable from 0 to 1 never results in the output changing from 1 to 0. Operations with this property are said to be monotone.
Nonmonotone Axioms
Nonmonotonicity enters via complement operation NOT as follows:
| (a) | (b) | ||
| x + ~x = 1 | x ‧ ~x = 0 | complements | (V) |
The above axioms (Ia) to (Va) and their dual (Ib) to (Vb) are the ones introduced by Edward V. Huntington in his paper "Sets of Independent Postulates for the Algebra of Logic" pp 293-293 in 1904 as postulates bearing the same reference numbers in its first set of postulates (his postulates Ia, Ib and VI are provided by the lattice basis and the fact that the set of Boolean values contains 2 distinct elements, {0, 1}).
These axioms are sufficient to prove all the other laws below:
Monotone Laws
More monotonous laws were introduced by Huntington:
| (a) | (b) | ||
| If x + y = x for all x, then y = 0 | If x ‧ y = x for all x then y = 1 | unique identity | (VII) |
| x + x = x | x ‧ x = x | idempotence | (VIII) |
| x + 1 = 1 | x ‧ 0 = 0 | annihilation | (IX) |
| x + xy = x | x (x + y) = x | absorption | (X) |
| x + (by + z) = (x + y) + z | x (yz) = (xy)z | associativity | (XIII) |
Nonmonotone Laws
And one more nonmonotonous law was also described in Huntington's paper (lawn XIV is not):
| If x + y = 1 and x ‧ y = 0, then y = ~x | unique negation | (XI) |
| ~(~x) = x | double negation | (XIV) |
De Morgan's Laws
However, whereas ordinary algebra satisfies the 2 laws:
(-x)+(-y) = -(x + y)
(-x)(-y) = xy
Boolean algebra satisfies De Morgan's laws:
| (a) | (b) | ||
| ~x + ~y = ~(xy) | ~x ‧ ~y= ~(x + y) | De Morgan's laws | (XII) |
These are the 2 last laws from Huntington's paper, and not surprisingly, form an indispensable tool when simplifying digital circuits involving AND, OR and NOT operations ("gates").
Other Nonmonotone Laws
Some other laws can be proven (make sure to display the "Proven properties" panel):
| (1) | (2) | |
| x + (~x + y) = 1 | x ‧ (~x ‧ y) = 0 | (a) |
| (x + y) + (~x ‧ ~y) = 1 | (x ‧ y) ‧ (~x + ~y) = 0 | (b) |
| (x + y) ‧ (~x ‧ ~y) = 0 | (x ‧ y) + (~x + ~y) = 1 | (c) |
| (x + (y + z)) + ~x = 1 | (x‧(y‧z)) ‧ ~x = 0 | (d) |
| y ‧ (x + (y + z)) = y | y + (x‧(y‧z)) = y(e) | (e) |
| (x + (y + z)) + ~y = 1 | (x‧(y‧z)) ‧ ~y = 0 | (f) |
| (x + (y + z)) + ~z = 1 | (x‧(y‧z)) ‧ ~z = 0 | (g) |
| ~((x + y) + z) ‧ x = 0 | ~((x‧y)‧z) + x = 1 | (h) |
| ~((x + y) + z) ‧ y = 0 | ~((x‧y)‧z) + y = 1 | (i) |
| ~((x + y) + z) ‧ z = 0 | ~((x‧y)‧z) + z = 1 | (j) |
| (x + (y + z)) + ~((x + y) + z) = 1 | (x ‧ (y ‧ z)) ‧ ~((x ‧ y) ‧ z) = 0 | (k) |
| (x + (y + z)) ‧ ~((x + y) + z) = 0 | (x + (y + z)) ‧ ~((x + y) + z) = 0 | (l) |
 Squonk42
Squonk42
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.