After the kiln's first run, it was found that it wasn't getting near as hot as I had hoped - not near as hot as the optimistic model had predicted either! In this log, we tweak the model parameters so that the time-dependent thermal model outputs a curve that is (somewhat) close to the experimental data from the kiln's first run. The script used for this is kiln_model_mathcing.py.
Here's the end result in graphical format:
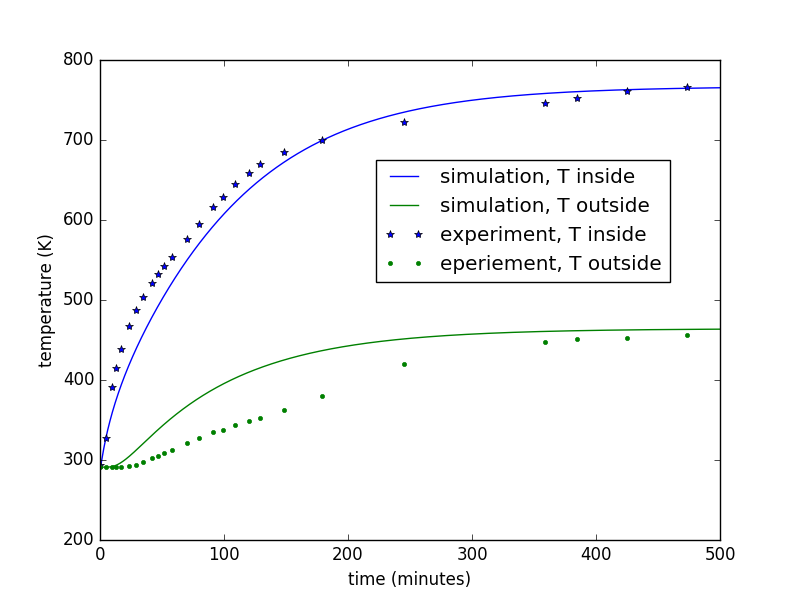
The important model parameters are the following:
rho = 2000.0 # density of wall material in kg / m^3
k = 1.3 # thermal conductivity of wall material in W / (m*K)
c = 400.0 # specific heat capacity in J / (kg*K)
h = 12.0 # convective heat transfer coefficient in W / (m^2 * K)
Q_dot_in = 1500.0 # heater power in watts
T_inf = 291.0 # ambient temperature in Kelvin
A couple things to note...
- These values are arrived at manually - I tweaked 'em around until the graphs looked about right.
- The simulated inside temperature matches the data OK, but the simulation of the outside temperature has it heating up much faster than the experimental data showed. I'm not sure why.
- The value of k is much higher than I had initially guessed. This might be due in part to the large gaps between bricks. Sealing the gaps might improve (reduce) this value.
- The values of h and c are somewhat lower than I had initially guessed.
So how hot will this thing get if we add a second heater? Here are the traces using the above parameters for a heater of Q_dot = 3000 watts:
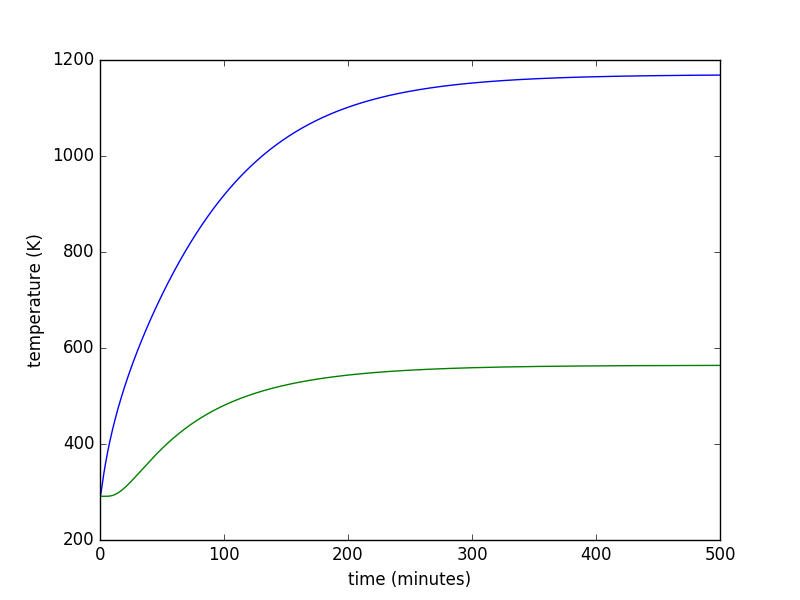
This gets up to about 1160 Kelvin, or 1628 degrees F, or 887 degrees C. Still not quite as high as I had wanted, but let's try it and see how high we get!
 Matt Moses
Matt Moses
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.