I've been working on the project for about a month now. I decided to post it to hackaday only recently, so I've got a lot of stuff to go over.
The first thing I did was build just a gamma ray detector. The output is hooked up to the trigger of a 555, which is also connected to a buzzer, so that I get a beep every time a gamma ray is detected. I accidentally bought an op amp with too high of an input bias current, so the detector does not work correctly right now. However, I'm ordering a new op amp which should get the detector working and beeping.

The PIN diode is inside the electrical tape below the voltage regulator. The white bodge wire is there because I accidentally flipped the inputs on the comparator.
Next, I experimented a bit with peak detector circuits. I realize now that the circuit from EEVblog #590 is probably not fast enough. I'll work more on the peak detector once I get the gamma detector working.
Finally, I bought a GPS module and arduino and got the arduino to detect the GPS's pulses to within 62.5 nanoseconds. I did this by setting up two timers and an interrupt. One timer ticks up when the other overflows. When the arduino detects a rising edge, it reads the values of the two timers, in addition to the count of the slower timer overflowing. You can see the code I used here.

I'm using a NEO 6M GPS module with an Arduino micro clone.

Here are my notes for how to measure pulses to within a single 62.5 nanoseconds. I use both timer1 and timer2.

Here is how I can measure to within 0.061ns. I can do this by integrating a new pulse the length of time between the pulse I'm measuring and the next tick of the arduino's crystal oscillator. Although I could try to implement this, it's a lot of extra work, and the GPS's pulses are only accurate to around 30 or 60ns anyway.
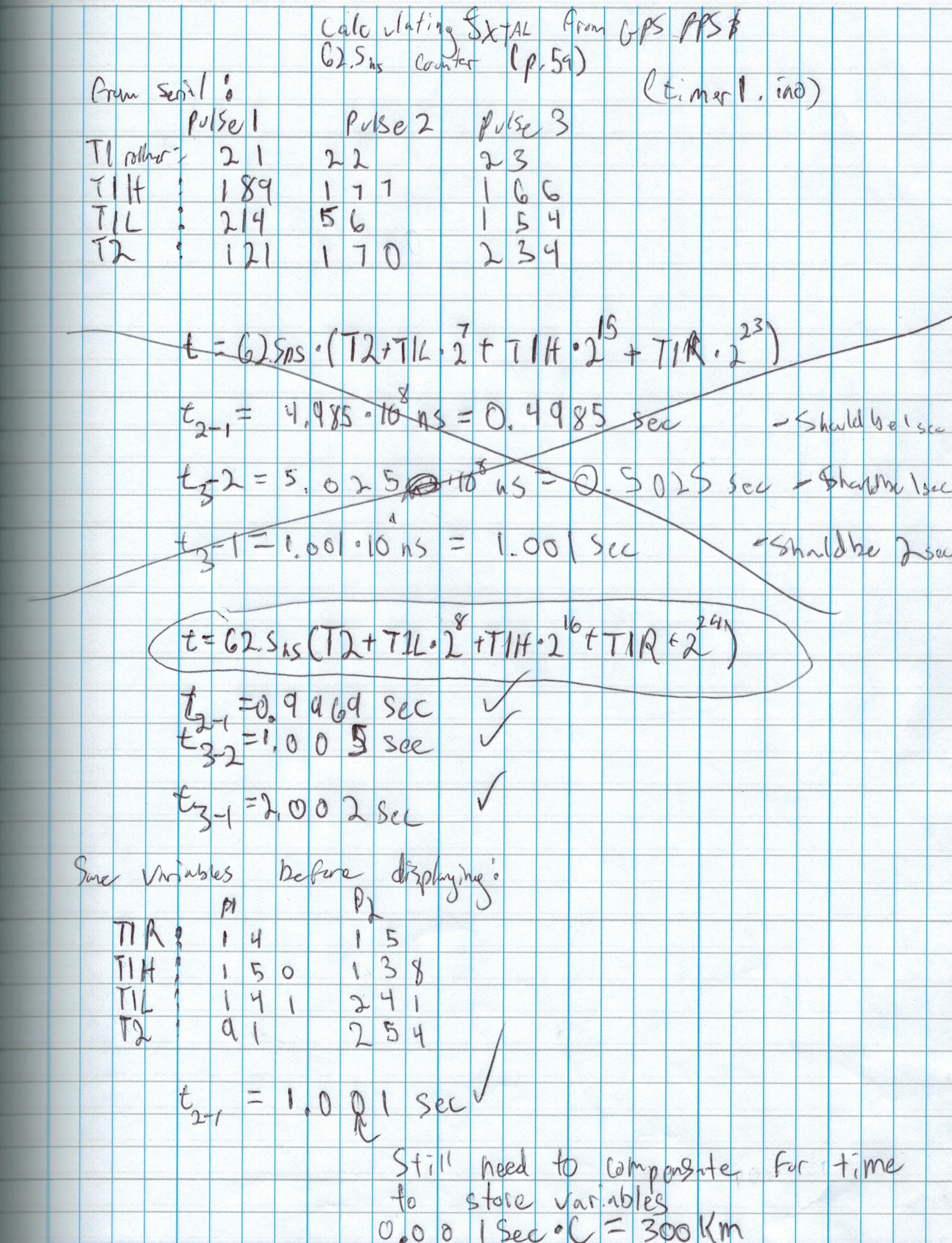
Here's proof that the timing works. My math got a bit messed up at first so that the results were around half of what they should be, but then I corrected my formula. You can see that the GPS and arduino's time are slightly different, which is what is expected.
 aelias36
aelias36
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.