Logs:
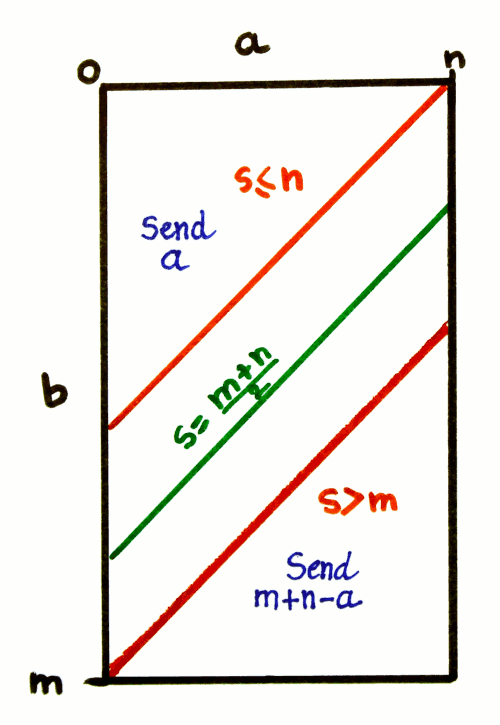
1. Extension to unequal boundaries
2. To reverse or to not reverse
3. Some lossy video compression
4. .
σα is a very simple algorithm that uses only basic operations over positive integers. Applications include:
- more compact colorspace decomposition
- new "fundamental transform" for the 3R algorithm
and certainly more to come...
Just like the µδ code, the name comes from data that are encoded:
- σ (sigma) represents the Sum
- α (alpha) represents one Addend (to be chosen)
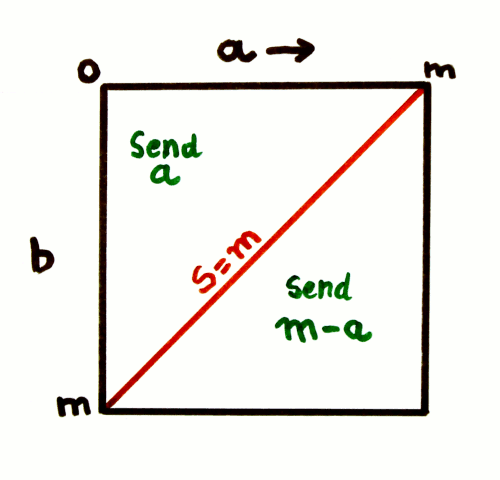
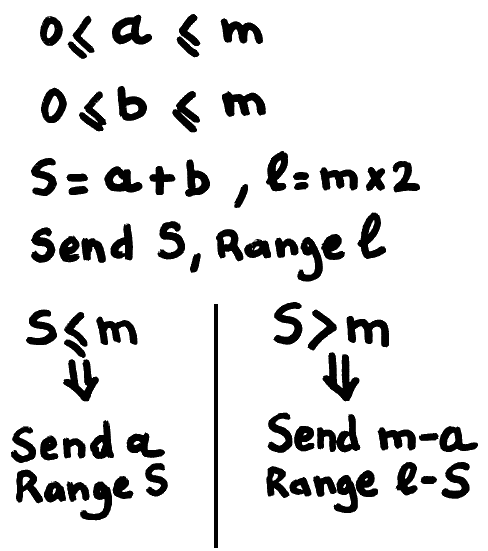
Encoding is as simple as
Decoding is straightforward:
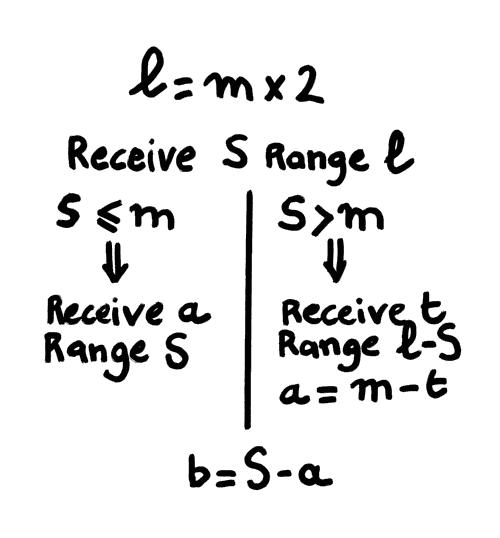
σα is used with VLC (variable length codes), in particular the similar-looking economy codes (also called phase-in codes or truncated binary codes) but an arithmetic encoder or a range encoder can also be used.
Why and how does this work ?
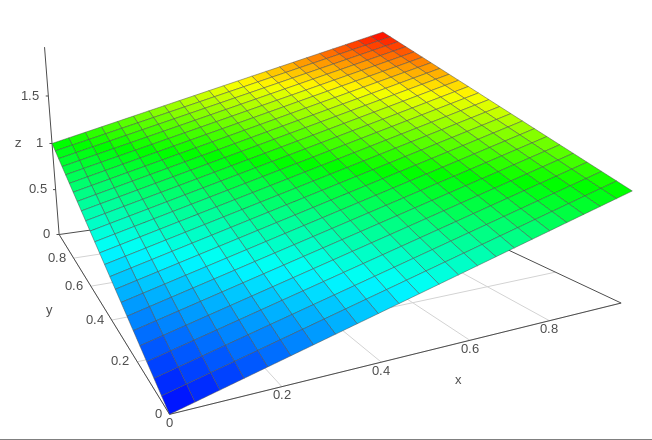
The z=x+y equation can be plotted in 3D, in the range 0..1 for each axis:
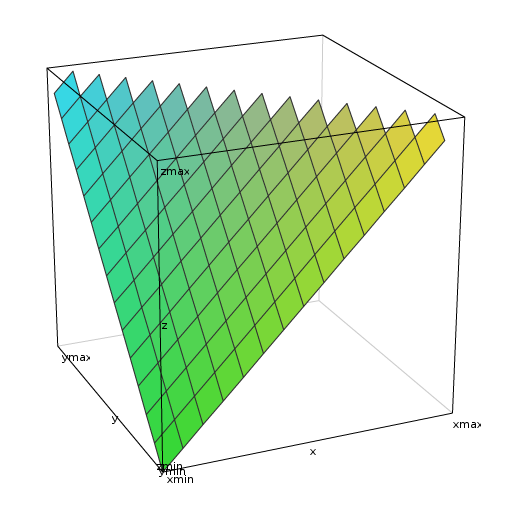
Without boundaries on x and y, the sum defines a tilted plane that is infinite. However, applying limits to the operands and the sum creates a triangle. This is actually one half of the whole plane, which is a rhombus encased inside two cubes:
(sorry, I couldn't get the scales right)
So the sum, when supplemented with the boundaries of the addends, puts an upper bound on the addends, which results in the triangle of the first plot (where x and y are restricted in the 0:1 range). To get the upper triangle, a simple symmetry is applied, and at the upper part, the triangle is getting narrower as x and y increase.
Now if you plot all the possible values that an addend, say, x, can have, depending on the sum y, we get another rhombus. What the algorithm's conditional subtraction does is to swap one half of the rhombus to create a triangle.

The above plot shows where the values m-a and l-S come from. The red shape can be encoded with a value that is x-sum but there is another, more interesting, possibility: by encoding 1-x, all the high values of x are transformed into low values. In the context of the 3R encoder, this solves a very nagging issue where consecutive high values eat up a lot of bits.
The following table shows the encoding for two numbers a and b bound to [0:7]. S is sent with the default range [0:14] The following number c = a || m-a is sent when it's not zero.
| b \ a | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 0 | S=0 | S=1, c=1 [0:1] |
S=2, c=2 [0:2] |
S=3, c=3 [0:3] |
S=4, c=4 [0:4] |
S=5, c=5 [0:5] |
S=6, c=6 [0:6] |
S=7, c=7 [0:7] |
| 1 | S=1, c=0 [0:1] |
S=2, c=1 [0:2] |
S=3, c=2 [0:3] |
S=4, c=3 [0:4] |
S=5, c=4 [0:5] |
S=6, c=5 [0:6] |
S=7, c=6 [0:7] |
S=8, c=0 [0:6] |
| 2 | S=2, c=0 [0:2] |
S=3, c=1 [0:3] |
S=4, c=2 [0:4] |
S=5, c=3 [0:5] |
S=6, c=4 [0:6] |
S=7, c=5 [0:7] |
S=8, c=1 [0:6] |
S=9, c=0 [0:5] |
| 3 | S=3, c=0 [0:3] |
S=4, c=1 [0:4] |
S=5, c=2 [0:5] |
S=6, c=3 [0:6] |
S=7, c=4 [0:7] |
S=8, c=2 [0:6] |
S=9, c=1 [0:]5 |
S=10, c=0 [0:4] |
| 4 | S=4, c=0 [0:4] |
S=5, c=1 [0:5] |
S=6, c=2 [0:6] |
S=7, c=3 [0:7] |
S=8, c=3 [0:6] |
S=9, c=2 [0:5] |
S=10, c=1 [0:4] |
S=11, c=0 [0:3] |
| 5 | S=5, c=0 [0:5] |
S=6, c=1 [0:6] |
S=7, c=2 [0:7] |
S=8, c=4 [0:6] |
S=9, c=3 [0:5] |
S=10, c=2 [0:4] |
S=11, c=1 [0:3] |
S=12, c=0 [0:2] |
| 6 | S=6, c=0 [0:6] |
S=7, c=1 [0:7] |
S=8, c=5 [0:6] |
S=9, c=4 [0:5] |
S=10, c=3 [0:4] |
S=11, c=2 [0:3] |
S=12, c=1 [0:2] |
S=13, c=0 [0..1] |
| 7 | S=7, c=0 [0:7] |
S=8, c=6 [0:6] |
S=9, c=5 [0:5] |
S=10, c=4 [0:4] |
S=11, c=3 [0:3] |
S=12, c=2 [0:2] |
S=13, c=1 [0..1] |
S=14 |
The table contains no identical pair of {S, c}, which proves that the encoding is fully reversible.
The size of S is fixed, in the range [0:2m], which adds one bit to the normal binary representation. This is a constant overhead that can't be avoided.
However the sum carries information about the addend a, which is then encoded as c. Depending on the value of S, c can use fewer bits, even no bit at all in the two extreme...
Read more » Yann Guidon / YGDES
Yann Guidon / YGDES