In this project the PIC micro controller has to playback the audio sample with different speed, lower and higher than the original sampling frequency.

From a first test test, with a code not really optimized, the PIC can access the memory (in any location), read a sample and send it to the DAC at a rate of more than 90 M samples per second.

My idea is to store the audio sample in a external SPI flash memory re-sampled at different rates.

For examples these rates could be: 0.25x 0.5x 1x 2x 4x etc...

The original audio sample is sampled at a rate of 44 K samples per sec and stored in the memory in the "rate 1x" table.

If it is needed to playback the sample at a speed of 1.5x the PIC will read the memory where it is stored the original sample (rate 1x) at 44/1x1.5=66 K samples per second.

If is needed playback at speed of 3x the PIC will read the memory where is stored the re-sampled audio at a rate of 2x with a speed of 44/2*3=66 K samples per second.

And so on. The playbacks speed will vary continuously according to the speed of the hand above the infrared sensor so the PIC should have the possibility to jump between different tables continuously.

In this moment I am studying how to convert the audio samples in different sampling rates. It is not a trivial thing but my advantage is that the program in the PIC will need to compute this only one time and save it in memory so it does not need to be real time.

To re-sample is necessary to filter the signal with a low pass at about half the sampling rate in the case of increase the sampling rate.

To intuitively understand why it is necessary i copy this picture:

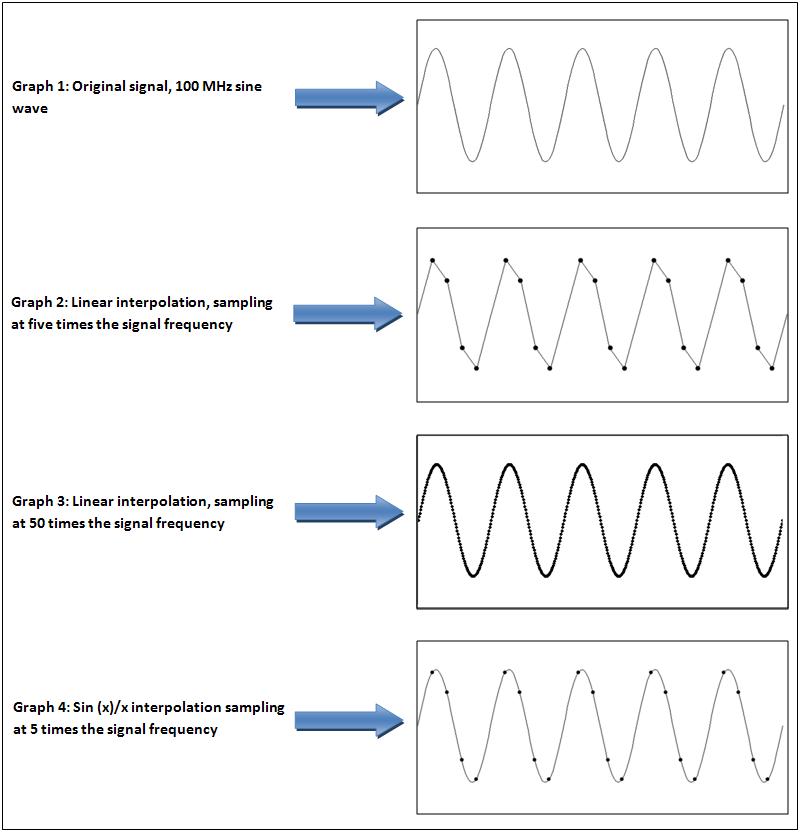
Now i am tying to understand the digital filter simulating it in python before write the actual program for the PIC.

This program takes sin wave (in this case 1000 samples), multiply every point of it for the value of the "windowed sinc filter", (in this case has 101 samples) sum up the results and find the peak value.

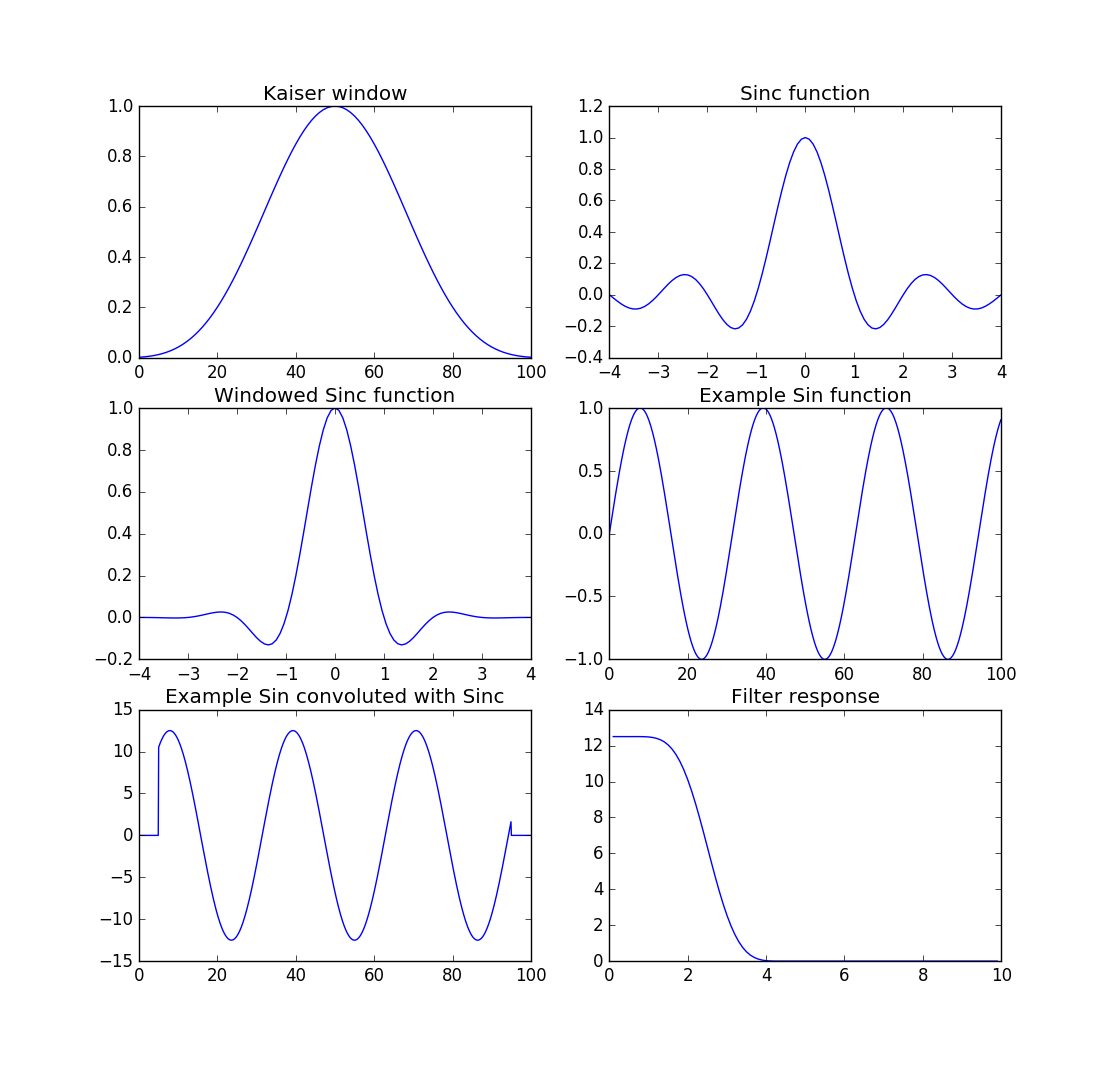
Then the same process is repeated changing the frequency of the sin wave. The filter response plot has on X the sin wave frequency and on Y the peak values of the filter output.

I am trying to understand if it necessary to apply the same process even when reducing the sample rate or it is enough a moving average filter.