So after the last update, I decided to toss trying to correct the pulley kinematics with math, and instead just cancel it out by creating virtual pulleys on the end effector.  

The cancelling out with two pulleys basically works like this.  As the angle changes whatever you lost in cable length by wrapping up onto one pulley you now gain in cable length by unwrapping from the other pulley.

By a virtual pulley I mean matching the shape the line wraps onto at any given angle with what that shape would be for the top pulley.  

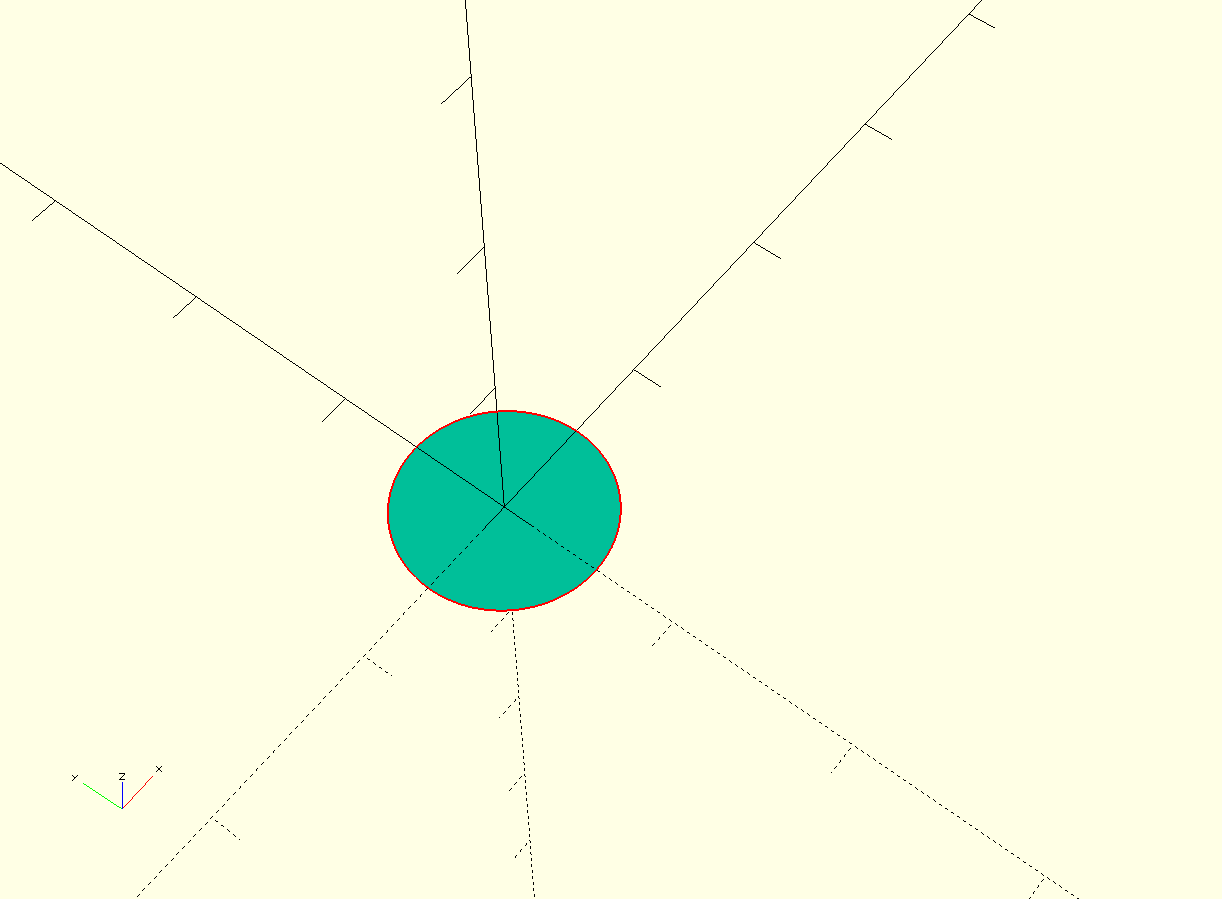
So start with the circular profile of the top pulley

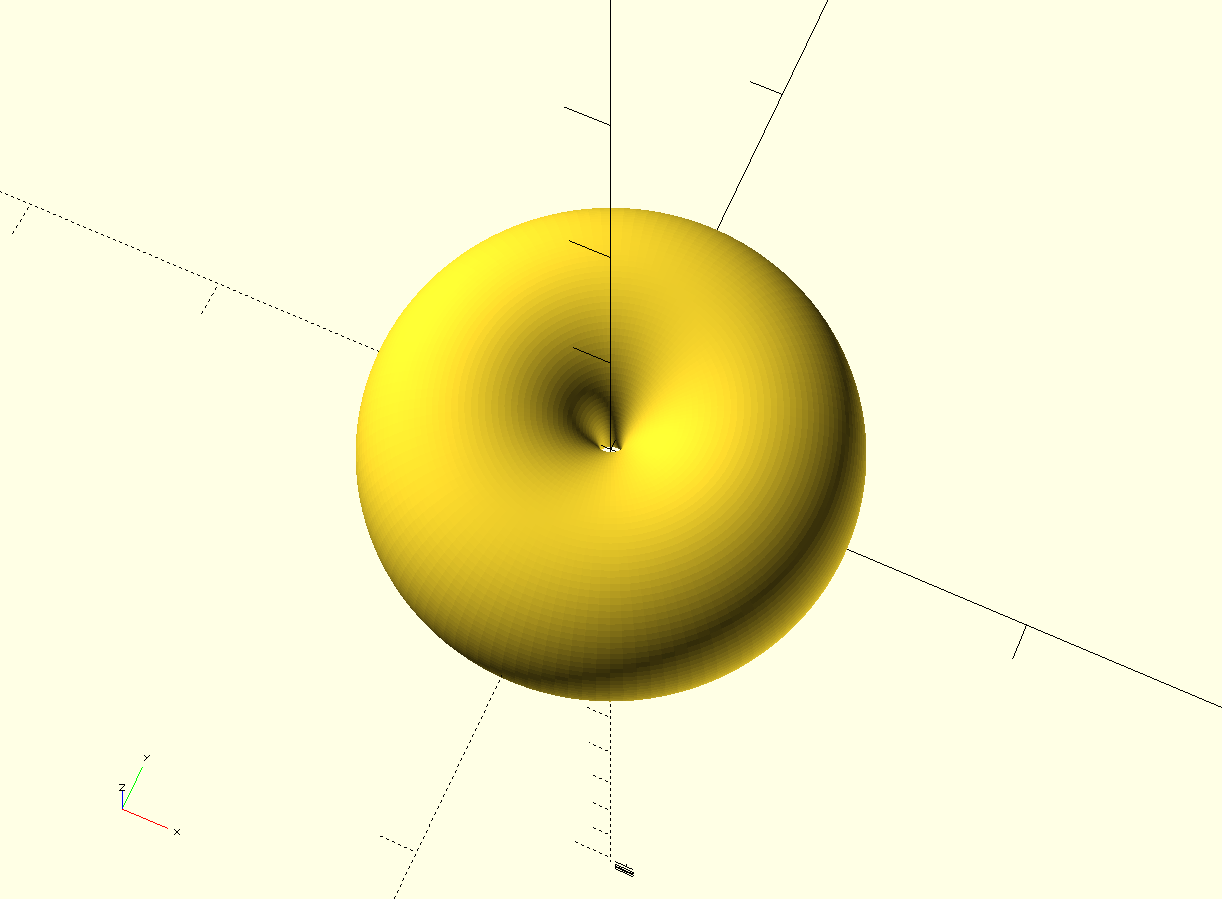
Then rotate this profile about the Z axis and you get a torus.  

Cut away the parts the cable will never touch due to machine constraints.

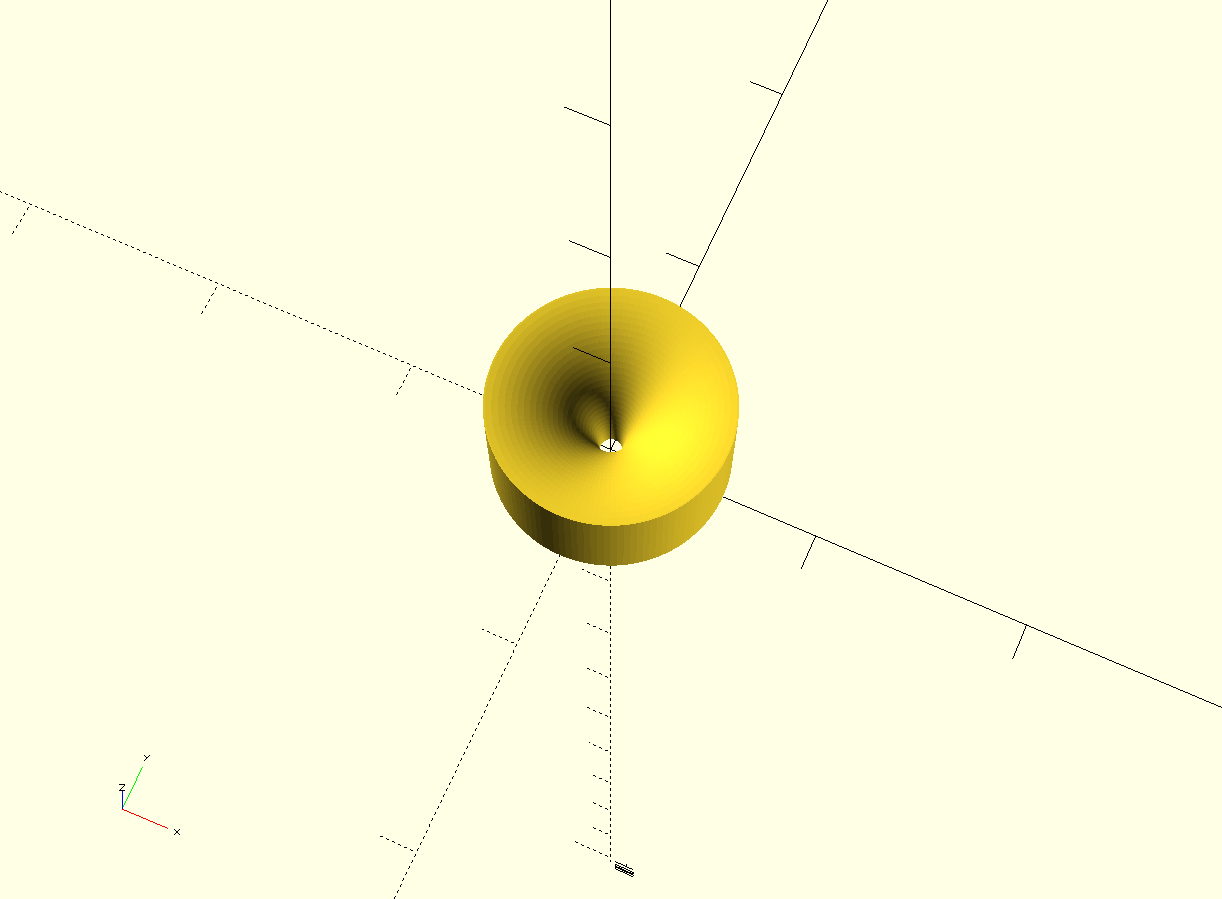
There, you got a virtual pulley.  Having the cable slide around the inner surface of this torus with radius R will be equivalent to having a pulley on a swivel with radius R.

Then I had a bit of a eureka moment.

I was thinking about how the top pulleys do not rotate to face the end effector, and what this would do to the effective cable length.

When the path to the end effector is in plane with the pulley, the proper shape for the virtual pulley at the bottom is a cylinder.  However, as the end effector moves out of plane towards the extremes, the lack of rotation of the top pulley ends up foreshortening the cable.  

Well, I think I can compensate for that: by elongating my virtual inverted pulley!  

This essentially allows me to vary the dimensions of the resulting virtual lower pulley based on the angle at which the cable is wrapping onto it.  

For example: Using a cylinder instead of a torus would result in a virtual pulley of R=R when the angle is straight on, but R=0 when the incoming angle is 90 degrees to either side.  

How much elongation do I need to compensate?  I have no idea.  I started with 20%.  It may require some other funky shape to be 'correct', but I approximated with an ellipse for now as that was easy to generate and thinking of what my pulley looks like from an angle, it might actually be right.

It may be difficult to solve for what is the correct shape, but I'm certain a shape which perfectly compensates for the error generated by the static upper pulley does exist.

Well that was a lot of explaining.  

If you are still with me, here is the new end effector with built in elongated error cancelling virtual inverted pulleys.

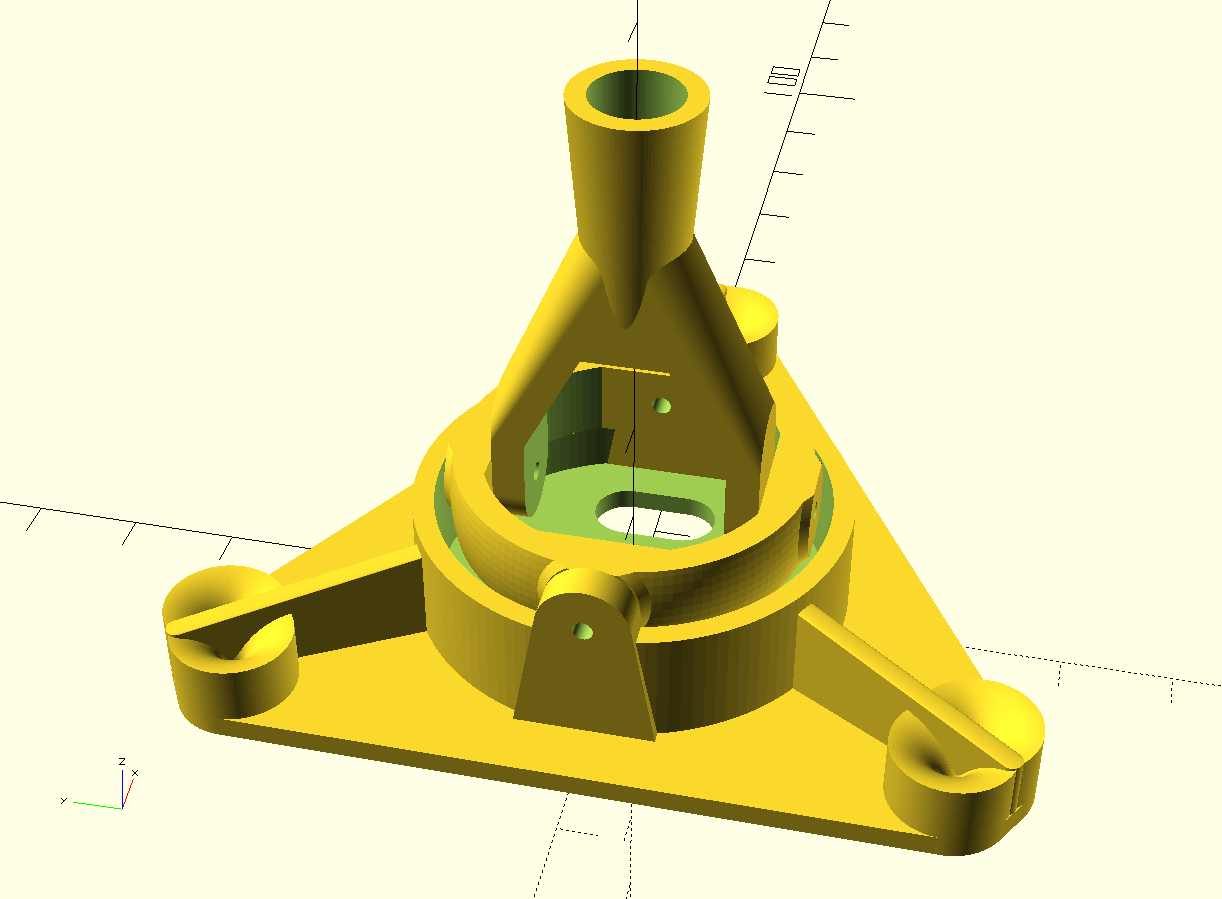
Take that you silly compensation math.