Introduction

I've been working with a fellow rocketeer in his understanding and development of 1" PVC motors and thought this would be a good time to share the process on this project page. There will be a fair amount of math, but nothing overly complicated.

Please note that this design process is for the 65/18/17 mixture of potassium nitrate, light corn syrup/sucrose that is used in my motors, known as flexfuel due to its more flexible nature that is less prone to the brittle fracturing found in pure sucrose motors.

If this design is used with a 65/35 plain sucrose motor a CATO will likely occur due to over pressurization.

1" PVC had been shown to be structurally sound up to 1000PSI for burns up to and past 3 seconds. We'll be using a lower pressure for safety.

Equations

Some simple equations are necessary to understand this post, they are simple geometry equations related to circles and rectangles.

K = Effective ratio of of specific heats of the exhaust products, obtained from combustion analysis

Walk Through of Motor Design

I'm going to work out the design of a 1" PVC motor with a .375" nozzle. These values are picked for a couple of reasons, the diameter of the case allows for higher pressure, isn't too large (good for testing), and is readily available. The bore size is half the diameter of the case, 1/2". This allows for a decently high thrust at ignition and a decent (75%) case loading. The nozzle is smaller than the bore size to limit erosive burning.

One of the main concerns when developing a motor is the risk of over pressurization. KN allows for us to scale motors of different sizes by designing them by the burn area and nozzle choke size. This directly correlates to maximum pressure the case will endure during firing.

A KN of 350 has empirically been shown stable with 1" PVC. We will be using a single inhibited progressive burn fuel grain. This is one continuous grain that is case bonded on the outside, and both ends are inhibited with a single cylindrical bore through the middle. This allows for ease of casting, resilience under stress, and has the feature of easier mathematical calculation.

Now that we know we have a 1" inner diameter PVC pipe that can handle a KN of 350, and a nozzle of .375", we need to know how long the fuel grain needs to be. The first thing we need is the area of the nozzle choke area.

Since KN = Burning Area / Nozzle Area we solve for Burning Area:

We put in our values:

So now we know that the maximum burn area needs to be 38.6563 in^2. The highest amount of fuel burning will occur just as the fuel burns out. This is essentially the surface area of the outside of the fuel grain, which is the circumference of the inner diameter of the 1" PVC multiplied be the casing length.

We know that the BA is 38.6563 in^2, and that our diameter is 1". We solve for L (d is removed because in our design equals 1):

Our case is now 12.3" long and has a bore of 0.5" with a KN of 350 in relation to our .375" nozzle choke diameter.

The next thing we need to calculate is the nozzle geometry itself. It's been shown that divergent nozzle half cone angle is most efficient at about 11 degrees, however angles up to 15 degrees are very effective and save on weight. So we will declare 15 degrees as our divergent half cone angle, but to determine how far the nozzle geometry should extrude past the choke we need to calculate the optimal expansion ratio. The convergent angle has shown to be almost negligible in effects, but a 45 degree angle will limit erosion near the steel washer insert.

This next equation is a bit overwhelming at first glance, but just bare with me here. It's from Richard Nakka and calculates the optimal nozzle expansion ratio.

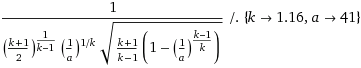
We are defining k as 1.16 from combustion testing, and a as 41 ATM (which is 600 PSI) for the internal chamber pressure. The pressure is derived from testing with KN values near 350, and gives a good starting point for calculation.

The result of this equation is: 6.52085. This is the expansion ratio that is optimum for our chamber pressure and fuel in relation to the area of the nozzle choke. Click here for the WolframAlpha Link to easily calculate this value.

So now we take our nozzle choke area, which is .1102 in^2 and multiply it by our expansion ratio:

This is the exit area from the nozzle that will match the ambient pressure to the pressure generated by our motor. To find the radius we do some more math.

Since this is still the radius, we double it to get our diameter.

This is a convenient number because .966 inches is very very close to our 1" inner diameter of our PVC casing.

Motor Design Finished Values

• 350 KN ratio
• 1" PVC casing
• 12.3" casing length
• .375" nozzle
• 15 degree half cone divergent angle
• 45 degree half cone convergent angle
• 6.648 expansion ratio
• .966 inch exit diameter

The initial KN value for this motor is right at 175. For faster chamber pressurization a sacrificial erosive nozzle can be cast in the choke. 3M fireblock caulking can be used to plug the nozzle choke, and a smaller nozzle drilled out. A 9/32" erosive nozzle will provide an initial KN of almost 310. As the burn progresses the nozzle will erode until reaching the concrete/steel washer. This method is not recommended for initial testing of this motor design due to over pressurization risks.

Conclusion

I hope that this helps some people in the understanding in the development of PVC motors that are safe and illuminates some of the math that is required in amateur rocketry.

Thanks to Steve Ghioto for some help with expansion math, Richard Nakka for a plethora of information on his website, and Dan Pollino for the flexfuel mixture.