The next natural step is to simulate the concept somehow. I chose to do this in MATLAB, and while it is neither open-source nor free (even though I, as a student, have free, unrestricted access to it from my university) you can likely do everything I did in MATLAB in GNU Octave, which is open-source.
The MATLAB simulation takes an input image and creates a scattered data interpolant of it. It then samples this image at non-discrete points (using the interpolant) that correspond to the radial sampling pattern of the sensor. It can also simulate sensor concentricity mismatch, the formula for which can be derived using Pythagoras' theorem (I'll have more detail on this soon). The radial samples are then used to create another interpolant from which the final image will be reconstructed.
The simulation was set up in such a way that a number of parameters can be changed with ease; sensor pixel count, samples around the circle, and final desired image size.
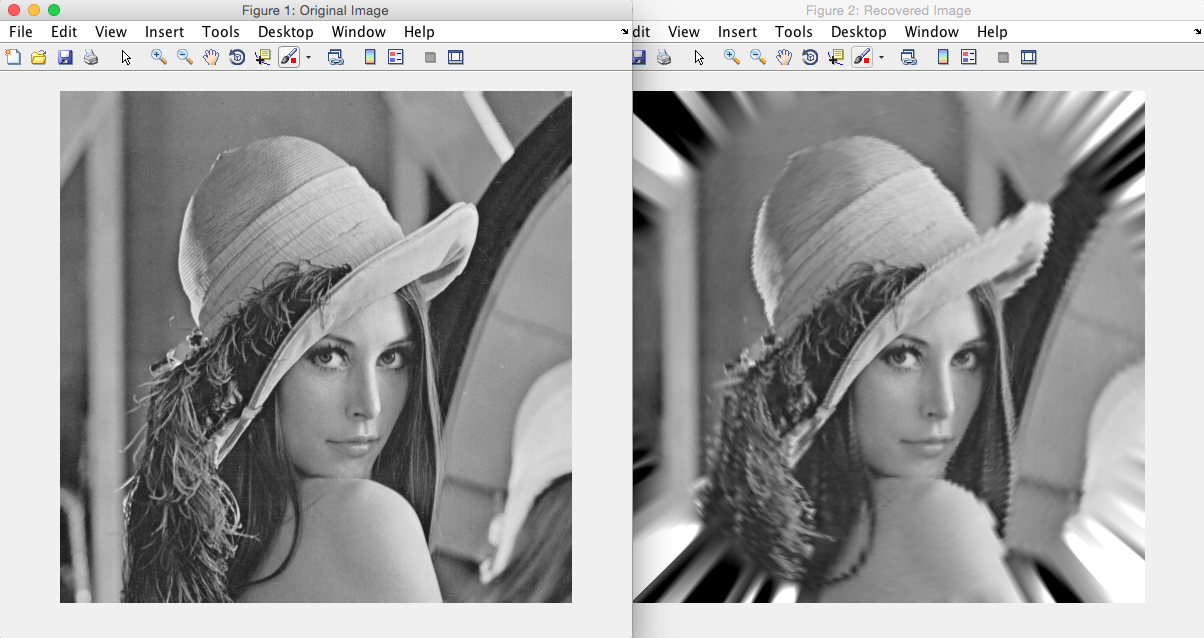
Below is a picture showing the original image (on the left) passed to the simulation and the reconstructed image (on the right) obtained at the end of the simulation. Notice how high frequency details (i.e. areas of high contrast or thin details) are lost further out from the centre due to the nature of radial sampling. The original image is the same size as the reconstructed image at 512x512 pixels, and the simulation was done using a sensor 128 pixels long, with 200 samples around the circle.
 A video simulation will be shown soon.
A video simulation will be shown soon.
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.