The core function of the OpenFence collar is to be able to contain livestock within a boundary, which means that it needs to know if the animal is inside the boundary. In order to implement the varying levels of alerts it also needs to determine how far outside the boundary it is.
The fence is defined as a varying number of points polygon, with each point being defined with it's latitude and longitude, and numbered in a clockwise direction. We then also have the lat/lon of the collar device from the GPS.
Download the code used in this log.
Step 1 - Distance between latitude/longitude points:
Various formulas are available to find the distance in metres between lat/lon points. I have summarised the differences below.
| Name | Haversine | Spherical Law of Cosines | Equirectangular Approx |
| Sqrts | 2 | 0 | 1 |
| Trig Calcs | 7 | 6 | 1 |
| Accuracy (100m) | - | 1E-5 % | 1E-10 % |
| Accuracy (1 km) | - | 2E-7 % | 7E-8 % |
| Accuracy (10 km) | - | 5E-10 % | 1E-5 % |
| Accuracy (1000 km) | - | ~0% | 0.02% |
Whilst Haversine isn't perfect, it has been used as the baseline for this comparison. As can be seen for distances less than 1 km Equirectangular Approximation was slightly more accurate and requires much less intensive calculations. For this application it seems to be the best choice.
double distanceEquir(struct position v, struct position w) { //Equirectangular Approximation
double p1 = (v.lonrad - w.lonrad)* cos( 0.5*(v.latrad+w.latrad) ) ;
double p2 = (v.latrad - w.latrad);
return 6371000 * sqrt( p1*p1 + p2*p2); //6731000 is the approx radius of the earth in metres
}
double distanceSpher(struct position v, struct position w) { //Spherical Law of Cosines
return acos( sin(v.latrad)*sin(w.latrad) + cos(v.latrad)*cos(w.latrad)*cos(w.lonrad-v.lonrad) ) * 6371000;
}
double distanceHaver(struct position v, struct position w){ //Haversine
double a = sin((w.latrad-v.latrad)/2) * sin((w.latrad-v.latrad)/2)+
cos(v.latrad) * cos(w.latrad) *
sin((w.lonrad-v.lonrad)/2) * sin((w.lonrad-v.lonrad)/2);
double dist = 6371000 * 2 * atan2(sqrt(a), sqrt(1-a)); //Metres
return dist;
}Step 2 - Test if within a varying number of points polygon:
After searching around for a while trying to find ways that this could be done in a way that used minimal computing power I found this excellent resource: http://alienryderflex.com/polygon/
I simply had to alter it a little to use structs as inputs.
bool pointInPolygon() {
//From http://alienryderflex.com/polygon/
//oddNodes = 1 means within the polygon, oddNodes = 0 outside the polygon.
int i, j=polyCorners-1 ;
bool oddNodes=0;
for(i=0; i<polyCorners; i++) {
if(((points[i].lat< me.lat && points[j].lat>=me.lat) ||
(points[j].lat< me.lat && points[i].lat>=me.lat)) &&
(points[i].lon<=me.lon || points[j].lon<=me.lon)) {
oddNodes^=(points[i].lon+(me.lat-points[i].lat)/(points[j].lat-points[i].lat)*(points[j].lon-points[i].lon)<me.lon);
}
j=i;
}
return oddNodes;
}Step 3 - Find which sides of the boundary we are outside:
First we calculate the fence normal vectors (Fn) for each side, such that the normal always points towards the inside of the boundary, and make sure it is unit length by dividing by the magnitude of the vector.
double distBehind(struct position p, struct position w, struct position v){
//Returns a negative if outside that boundary.
double Fplat =w.lat;
double Fplon =w.lon;
//Calculate the unit length normal vector: Fn
double Fnlat = w.lon-v.lon; // y'
double Fnlon = - (w.lat-v.lat); //-x'
double mag=sqrt(sqr(Fnlat)+sqr(Fnlon));
Fnlat /= mag; //Unit length
Fnlon /= mag;
//p-Fp
Fplat = p.lat- Fplat; //Reuse variables
Fplon = p.lon - Fplon;
//Return the dot product
return Fplat*Fnlat + Fplon*Fnlon;
}Then we find the vector of the animal p to a point on that side of the fence. We then use the dot product of these two vectors to find the d. This can then be used to determine the approximate distance to each side the collar (p) is by multiplying by 100,000. If the value of d is negative then it is outside that side of the boundary.
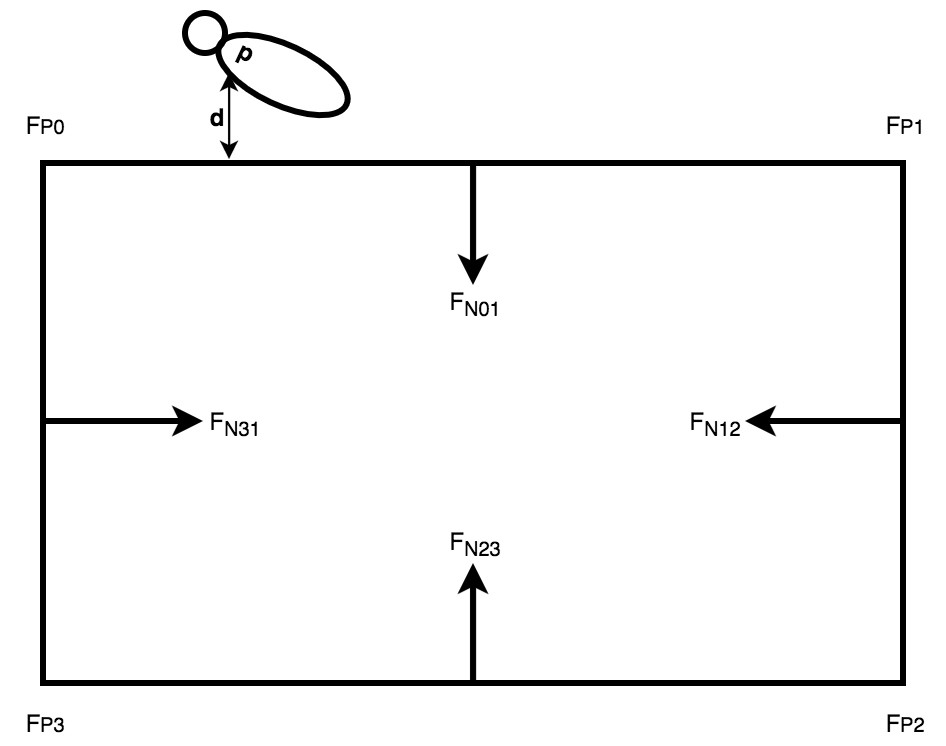
Step 4 - Find the distance to the "most negative" side:
I'm unsure if I will keep this step as the value of d calculated above is usually within a similar region as the Equirectangular distance. However at this point I have implemented to also use the Equirectangular Approximation as mentioned above find the shortest distance to the side of the fence we are outside.
The point must be projected onto the fence line and then the distance to this point is calculated. However additional checks must be performed to make sure the point is within the ends of the line segment, if it is not then we use the distance to the closest end.

//Step 4: Get an accurate shortest distance to a side of the fence
double dist2segment(struct position p, struct position v, struct position w){
//Check if the two side points are in the same location (avoid dividing by zero later)
double l = distanceEquir(v,w);
if(l==0) return distanceEquir(p,v);
//Find the max and min x and y points
double minx = MIN(v.lat, w.lat);
double maxx = MAX(v.lat, w.lat);
double miny = MIN(v.lon, w.lon);
double maxy = MAX(v.lon, w.lon);
struct position projection;
if(p.lat<minx && p.lon<miny){ //p does not fall between the two points and is closest to the lower corner
projection.latrad = degrees2radians(minx);
projection.lonrad = degrees2radians(miny);
}else if(p.lat>maxx && p.lon>maxy){ //p does not fall between the two points and is closest to the lower corner
projection.latrad = degrees2radians(maxx);
projection.lonrad = degrees2radians(maxy);
}else{ //p does fall between the two points, project point onto the line
double x1=v.lat, y1=v.lon, x2=w.lat, y2=w.lon, x3=p.lat, y3=p.lon;
double px = x2-x1, py = y2-y1, dAB = px*px + py*py;
double u = ((x3 - x1) * px + (y3 - y1) * py) / dAB;
double x = x1 + u * px, y = y1 + u * py;
projection.latrad = degrees2radians(x);
projection.lonrad = degrees2radians(y);
}
//Return the distance to the closest point on the line.
return distanceEquir(p, projection);
}Step 5 - Combine:
Green boxes have been covered in this log and have been tested both on the computer in the attached C code and walking around on an oval with the functions running on an Arduino with GPS.
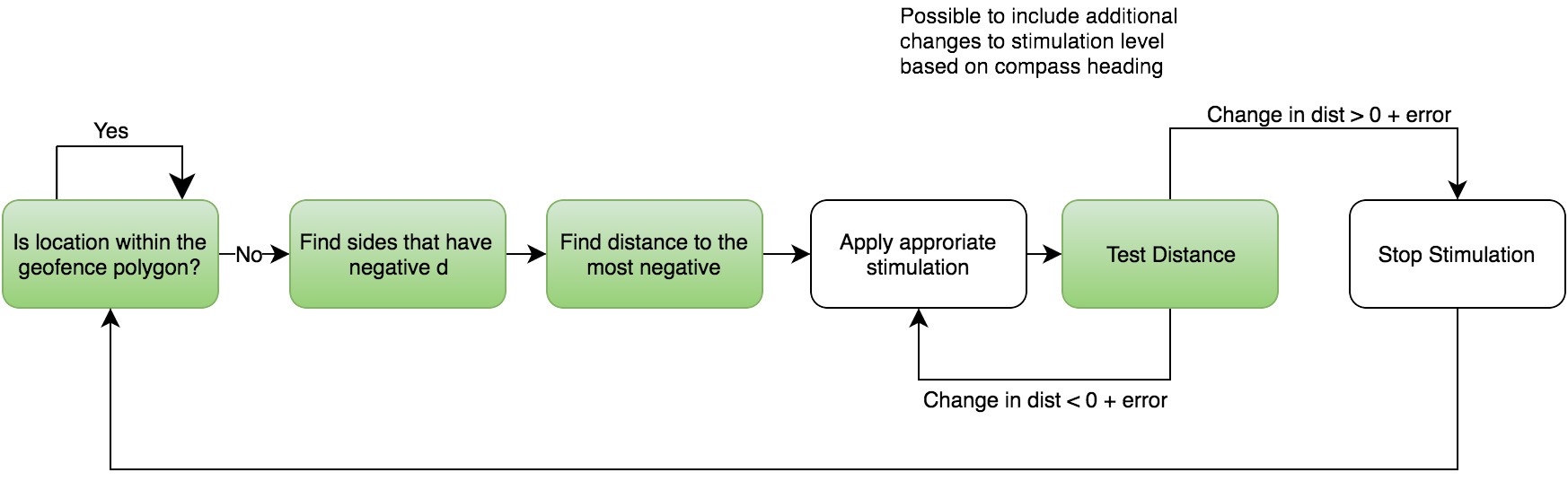

 Alex Muir
Alex Muir
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.