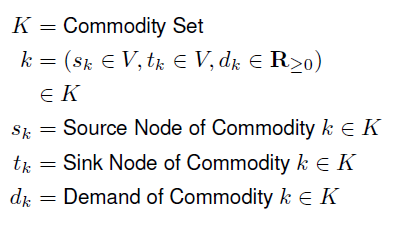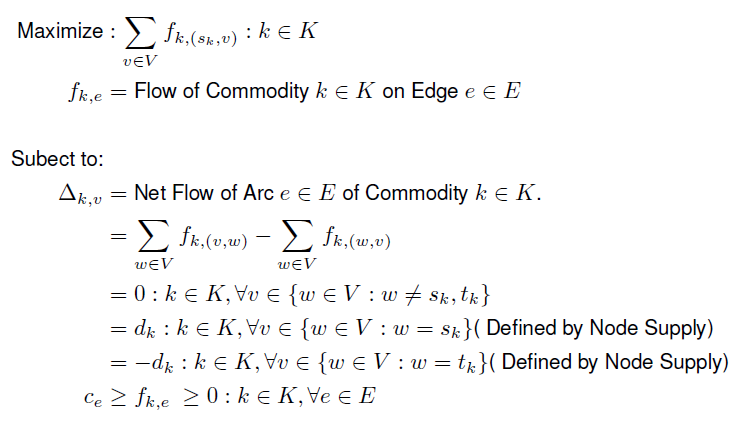-
Maximum Flow Problems in MATLAB and LEMON ( C++ )!
10/09/2016 at 23:54 • 0 commentsBefore I begin, I need to point out that this log follows after My Introduction to Linear Programming and GPLK. So, any explanation having to do with why I'm adding logs on flow network problems and references to the topics, I will either skim over or entirely avoid here! But, the relevant take away from the previous log is that I've been teaching myself the many ways Maximum Flow ( MFP ) and related problems can be solved, which lead me to the Linear Programming ( LP ) optimization with GNU MathProg ( GMPL ) and its C API, the GNU Linear Programming Kit ( GLPK ).
However, even though I find GMPL to have the most intuitive syntax, I find there are a lot of limitations with GMPL! The GLPK API is nice in that I get to use the language I'm most familiar with, but the API forces the user to always formulate their problem in the standard LP form. This leads me to the focus of this post.
The Idea: Learn how to solve Maximum Flow Problems in MATLAB and LEMON ( C++ )
The tools that sparked my interest the most are MATLAB, LEMON, and Boost Graph Library ( BGL ). MATLAB, to me is the most convenient language / development environment when it comes to reducing the time it takes to write the code! Heck, it has carried me throughput my years as an undergraduate and also as a graduate. But, I actually have more experience in C++, and so I decided to look into two possible graphing libraries. From what I can gather, two of the most well known graphing libraries are LEMON and BGL, and for a moment I was really tempted to go with the latter. But, a comment on stack overflow suggested I may run into issues with the documentation. I should point out that comment was posted back in 2011. So, there's a good chance BGL is better documented today. In the end I decided to learn LEMON over BGL, based primarily on how intuitive the libraries are to understand.
First and Second Implementations: MCFP-CF Solved with MATLAB and LEMON
Basically spent part of last week and a lot of the weekend reading through documentation and implementing my own examples, for both MATLAB and LEMON. In this log, I present three of those examples. The first two solve the same Concurrent-Flow variant of the Multi-Commodity Flow Problem ( MCFP-CF ) with LP, as was done in the previous log. However, in this log I do a MATLAB and C++ implementation.
For those who don't already know, MATLAB allows for dynamic access to the members of a structure. Effectively, this is how MATLAB implements associative arrays ( e.g. Python Dictionaries, C++ map class, etc. ). Not sure of its performance, but it can make very nasty looking code look a lot less nasty. Unfortunately, the first time I wrote the MATLAB implementation, I COMPLETELY forgot MATLAB could do this, and as a result, ended up with so many undesirable for-loops, something to be avoided in MATLAB. The second revision, whose MATLAB source code can be found here, is a lot cleaner! Granted, it probably runs poorly since I focused on making the code readable rather than efficient.
The C++ implementation can be found here. I should point, LEMON doesn't do any of the LP itself. Instead, it interfaces to other solvers. In my case, it just defaults to GLPK! Compared to the MATLAB implementation, the C++ solution is a lot longer in terms of number of lines, excluding comments and declarations! And, even after becoming familiar with the LEMON library, it definitely took more time to write the C++ implementation! But, C++/C solutions seem more prevalent in NoC-related research ( that I've looked at ), probably because of the gains in performance. The C++ implementation is also more accessible to people, since anyone can freely download the compilation tools and the required libraries.
Third Implementation: MCFP-CF Solved with Iterative Solution with LEMON
This final example solves the same MCFP-CF, but with a slightly different approach. The idea behind algorithm I actually got from this dissertation. Before I jump into any details, the full source code can be found here, which does include documentation on pretty much what I'm going to explain here.
With any good explanation on a mathematical algorithm, it's always a good idea to define all nomenclature --- even if the algorithm is simple and/or the nomenclature is somewhat obvious ( in my opinion, I should add ). So, like in the last post, the network has the following form.
A small difference between this log and the last is that there's a capacity associated with each arc in the network, instead of a single capacity associated with every arc. Now, the commodities are once again defined as the following.
An important step in the algorithm is to solve the Maximum Flow Problem ( MFP ) for a given commodity and the graph.
Didn't rely on LP this time around. Instead, I simply depended on a LEMON algorithm that solves the Circulation Problem, but constrained to solve the MFP. But, the iterative algorithm is finally presented below!
The algorithm is actually pretty simple. Basically, in order of the commodity with the largest demand, determine the corresponding flows by solving the MFP and update the capacity of the arcs for each set of flows. It yields similar results to the MCFP-CF solved with LP. Well, only tested them both for simple cases, honestly. Later, I will do a more comprehensive test!Cheers!
-
My Introduction to Linear Programming and GPLK
10/05/2016 at 03:38 • 0 comments( An observant reader noticed an inconsistency with the MCFP-CF model! I modified the GMPL code on GitHub and the snippet presented in this log, but I will later modify the text in this log in order to reflect the changes made the to code! )
So, I can already foresee the "Embedded Systems" project becoming a dump for anything and everything related to engineering. I sort of want a place where I can post small blogs on things I find interesting, and HACKADAY just seems like the ideal place. Plus, I find it really helps to understand an idea by explaining it in your own words. Now on to what this log is supposed to be about!
The Idea: Learning Linear Programming and GMPL
Before I elaborate on the idea behind this log, I first want to point out why I am posting this particular log, and also explain some of my long term goals. At some point, I aim to create a project page, detailing the research project I have been working on for my degree. Not going to explain any specifics in this post, but a crucial facet of the work is to implement an on-chip distributed network, optimized for satisfying real-time constraints ( for reasons that will be explained in the future ). The pertinent research area related to that facet is Network-on-Chip ( NoC ), particularly the area having to do with satisfying Guaranteed Services ( GS ). A good introduction to the area can be found here!
However, my background is in Computer Architecture and Embedded Systems! Although I'm not new to the idea of NoCs ( effectively, let's develop on-chip communications to utilize switching networks, such as that on which the Internet depends ), I still have a lot to learn regarding the theory, specifically the area having to do with circuit switching and GS quality of service. More importantly, I need to learn the tools needed to understand a lot of that theory, which brings me to a somewhat new, though fascinating area of mathematical optimization: Linear Programming ( LP ).
From my basic understanding, LP problems are always defined as the optimization ( either maximizing or minimizing ) an objective function with respect to a set of constraints, which are typically linear inequalities but can include equalities.
Actually, I'm not sure whether or not it's okay to count equalities as legitimate constraints, since every source I've checked defines the constraints as a bunch of inequalities. In spite of those sources, though, there does appear to be a lot of problems for which an equality is needed. So I'll go ahead assume equalities are somehow implied!
( until someone much smarter than I decides to yell at me, of course! )
In addition to learning the fundamentals of LP, I want to also test my understanding through trying to recreate the results of various LP problems related to my application. The tool that appears to be most common for modeling and solving LP problems is the GNU Mathematical Programming Language ( GMPL ) ( which is partially derived from AMPL ). I was initially debating whether or not to use MATLAB's LP tools. For now I will stick with GMPL since, from various online postings, it seems the general consensus is that GMPL/GLPK runs comparatively faster and is more common for my application.
The Theory: GLPK API and Multi-Commodity Flow Problem.
I decided to first get practice with both the GLPK API ( C/C++ interface for GMPL ), as well as GMPL. And, as it turns out, programming with the GLPK API is a TEDIOUS experience; many function calls are needed to implement the simplest of models. Worst of all, the API doesn't appear to have any way using set theory, other than importing a GMPL model!
This leads me to the "project" I want to present! As a way to learn how bandwidth across a network can be allocated according to the demands of the network, I decided to implement the Multi-Commodity Flow Problem ( MCFP ), optimized for Concurrent Flow ( CF )!
What does all that mean, though? Well, from my basic understanding, the problem involves a network in which data needs to be transmitted between source and sink nodes. Judging from the references, the network seems to be typically represented as a directed graph, but MCFP does have a variant for which the network is a undirected graph. I simply chose the directed variant in my implementation. Commodity basically represents the data that can be transmitted over the network. Specifically, commodity is defined by a source node, a sink node, and its demand on the network. The source and sink nodes inject and remove commodity from the network, respectively.
So the goal of MCFP is to determine what the flow of each commodity is over each edge in the network that optimizes the objective function, subject to a set of constraints. Since the flow of commodity can represent utilized bandwidth and capacity can represent available bandwidth, it makes sense to implement the CF variant. Thus, the objective is to maximize the lowest percentage of injected commodity over demand ( I could not figure out how to best word this for the life of me lol ).
Last and certainly not least are the constraints. There are basically three. The first ensures the total flow over an edge does not exceed a chosen capacity. The second, I like to refer to as the conservation constraint, in reference to the Law of Conservation of Energy. In short, the net flow of a node ( in other words, the sum of a commodity flowing into and out of the node ), should equal zero if the node isn't a source or a sink. The final constraint ensures the demand is always met. If the node is a source, then the net flow should equal positive demand of the source node's commodity. This represents commodity being injected into the network. If a sink, then the net flow should equal negative demand of the sink node's commodity, instead. This represents commodity being removed from the network.
That's basically it!
The Implementation: GMPL
As for actually solving MCFP-CL for a given network, I of course used GMPL. Since the language is very concise, I'll include the model below as a snippet. But, the full thing with the comments can be found here.
# Multicommodity Flow Problem for Directed Networks, ## Optimized for Concurrent Flow set V; set E, within V cross V; set K; param s {K}, symbolic in V; param t {K}, symbolic in V; param d {K}, >= 0; param c, >= 0; var f {K,E}, >= 0; var dstar {K}, >= 0; # Conservation Constraint. s.t. conserve_ct { k in K, v in V } : ( sum { w in V : (w,v) in E } f[k,w,v] ) - ( sum { w in V : (v,w) in E } f[k,v,w] ) = if ( v!=s[k] and v!=t[k] ) then 0 else if ( v=s[k] ) then -dstar[k] else if ( v=t[k] ) then dstar[k]; # Demand Constraint. s.t. demand_ct { k in K } : d[k] <= dstar[k]; # Flow Constraint. s.t. flow_ct { k in K, (w,v) in E } : f[k,w,v] <= dstar[k]; # Capacity Constraint. s.t. capacity_ct { (v,w) in E } : ( sum { k in K } f[k,v,w] ) <= c; # Optimization Objective. var z, >= 0; s.t. conc_ct { k in K } : dstar[k] / d[k] - z >= 0; maximize obj : z; data; # Example. set V := A B C; set E := A B B C C A; # Capacity of each edge. param c := 10; # Finally, let's define ## the commodities. param : K : s t d := k0 A C 0.5 k1 B A 0.5;
Might actually take more time to learn GMPL and possibly AMPL ( but a quick Google search reveals AMPL costs money, so maybe not )! From my brief experience, GMPL seems to have a very concise and clean look to it, which I like a lot when it comes to relating the model back to the mathematical expressions.
Anyways, to test the model, I ran it against several simple flow networks with commodities. Still learning how to automate the generation of more complex topologies and how to easily check such topologies with their commodities. So for now I will only demonstrate a single test case. Let's consider the following directional ring network for which the capacity of every edge is 1.
![]()
Let's say the commodities are the following.
K s t d k0 A C 0.5 k1 B A 0.5 After applying the well-known Simplex Method ( with GMPL, of course ), the following is the results.
Variables Result f_{k0,(A,B)} 0.5 f_{k0,(C,A)} 0 f_{k0,(B,C)} 0.5 f_{k1,(A,B)} 0 f_{k1,(C,A)} 0.5 f_{k1,(B,C)} 0.5 z ( objective value ) 1 GMPL also returns the final results for net flow and how much of the total capacity of each edge is utilized! But, ( believe or not ) I'm trying not to let this post go on for too long!
This obvious example is simple to check, though. First of all, summing together the flows for the same edges reveals the capacity constraint is satisfied. Looking at f_{f0,(B,C)} and f_{k1,(C,A)} shows the conservation constraint is met! Finally, the demand constraint is also satisfied, as evidence by the fact the net flow going out of k0's source is equivalent to the net flow going into k0's sink. The same is true for k1.
The objective value of 1 also makes sense. Recall, the objective value describes the lowest ratio between amount of commodity injected into the network over the commodity's demand. Since, the problem is constrained such that the demand is always met, the lowest the objective value can be is 1, implying the amount of commodity injected into the network is at least equal to its demand.
One last check!
What if the demand of a commodity is increased such that a single edge in the ring network wouldn't have the capacity to meet the total demand? In a directed ring network, where there's only one direction commodity can flow, increasing any of the demands will just cause the solver to fail and return an objective value of 0! This failure is actually a good thing, considering there's no other alternative paths in a directed ring!
Annnd, that finally concludes this log!
The Conclusion: These Logs are Way Too Long.
Really need to work on a way to make these posts shorter. But, I sure as hell enjoy writing them! Next time, I will probably break up longer logs into several shorter logs. If you managed to get this far, please look at the references! Pretty much my entire knowledge base on LP and related problems and algorithms came from those references!
The References:
https://www.math.ucla.edu/~tom/LP.pdf
http://www.purplemath.com/modules/linprog.htm
https://www3.nd.edu/~jeff/mathprog/
http://www.es.ele.tue.nl/~kgoossens/Stefan12PHD.pdf
http://www.columbia.edu/~cs2035/courses/ieor6614.S16/multi.pdf
-
SREC Bootloader and lwIP Stack on the Nexys 4
10/03/2016 at 10:14 • 0 commentsI briefly mention this in the video itself, but this project will play a small role in a collaborative project I am planning to do with fellow HACKER @Neale Estrella. So, I won't discuss much detail in this log.
-
Multi-Channel DMA and Box-Muller Algorithm
09/20/2016 at 02:23 • 0 commentsOkay, so this project has very little to do with Linux. In fact, is has nothing to do with Linux, or Zynq! I’m actually planning to change the format of this “project” ( or perhaps the project’s format has already been changed, depending on when you are reading this log ). I regularly do smaller projects as a way to focus on learning something knew. And, since I don’t want to end up adding a million different projects, this project page will be changed to include any sort of small embedded project! From this point forward, the individual projects under this project page will be added as separate logs!
On to what this log is really about…
The Idea: Learning the DMA Scatter Gather and Multi Channel Modes and Generating Samples from a Normal Distribution in a FPGA!An important component in virtually any computer system is Direct Memory Access ( DMA ), how a peripheral can directly access main memory without the need to depend on a host device. Clearly, a very useful and practically necessary component. For my applications using Xilinx FPGAs, external memory access with the Xilinx AXI DMA is the fastest ( and simplest ) method compared to alternative solutions, for instance directly implementing a full master AXI interface ( excuse the redundancy )! So, I regularly use the DMA core so that my cores can access external memory. But, before the completion of this project, I would only use the AXI DMA to perform simple transfers, not relying on the more advanced, though more useful features.
Thus, the main idea behind this project is to learn how to perform Scatter Gather I/O with the DMA! Little did I know before doing this project Scatter Gather I/O is not specific to the Xilinx AXI DMA core but in general refers to multiple input and output operations executed from an array ( or vector ) of buffers. However, because I want to have multiple peripherals in the FPGA access memory, learning the SG mode of operation also includes Multi Channel mode.A secondary objective is to do more with High Level Synthesis ( HLS ). So, I decided to implement the polar form of the Box Muller algorithm for generating samples from a Normal Distribution in the FPGA!
The Theory: Box Muller AlgorithmNot much theory on SG operations, really. I will talk a bit more about my experience with SG in the implementation section of this log.
As briefly mentioned, the Box Muller algorithm is a method for generating normally distributed samples from uniformly distributed samples. There are two basic forms of the algorithm, the first of which relies on trigonometric operations, which are costly operations. The second form, referred to as the polar form, eliminates the trigonometric operations completely. I will only show the algorithm for the polar form here since this is the algorithm that is actually used.
Pretty simple, right? With HLS, it’s almost trivial to implement! I will discuss a bit more about the implementation in the next section!
The Implementation: Generate a Tone and Make Some Noise!
All the project does is generate a single tone and add normally distributed noise to the signal. The volume of the tone and noise can be changed with the pushbuttons, and the tone and the signal can be toggled altogether with two slide switches. The target hardware includes the Digilent Nexys 4 DDR development board, which contains a Xilinx Artix-7 FPGA. Connected to the board is a Digilent Speaker Peripheral Module, which uses an amplifier that can be driven by PWM.
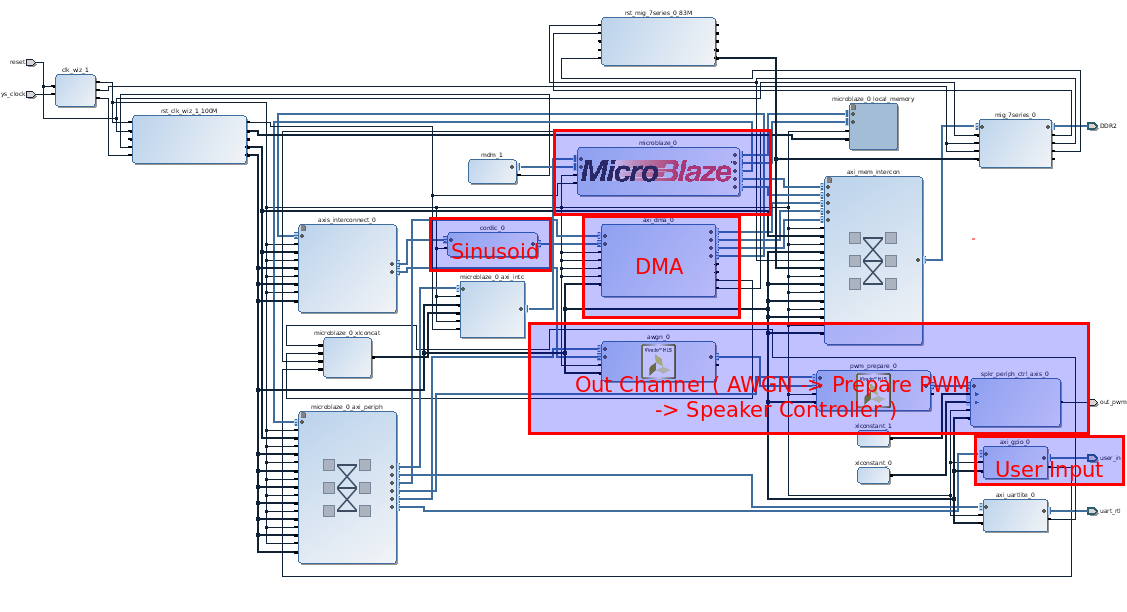
![]() The general flow of the system is a follows. The host device, the soft processor MicroBlaze, first configures all the peripherals in the system. Through the DMA, a CORDIC core is then used to generate the samples of the sinusoid which represents the tone. Once the samples are acquired, several vectored SG write operations are configured to ensure the DMA will continuously feed the sinusoidal samples to the Out Channel.
The general flow of the system is a follows. The host device, the soft processor MicroBlaze, first configures all the peripherals in the system. Through the DMA, a CORDIC core is then used to generate the samples of the sinusoid which represents the tone. Once the samples are acquired, several vectored SG write operations are configured to ensure the DMA will continuously feed the sinusoidal samples to the Out Channel.So, my main challenge in this project can be boiled down to misunderstanding how the SG and Multi Channel modes work in the DMA. The reason for this misunderstanding can then be boiled down to my habit of skimming through documentation, particularly datasheets --- particularly LONG datasheets. I don’t think this is necessarily a bad habit, since in many situations the datasheet is mainly a reference. But, it can be dangerous, clearly. I’m sure any programmer / engineering / hobbyist / everyone hates having to read through a 100 page document just so they can take advantage of a core ( or class, function, device, etc. ) whose purpose can be summarized in a single sentence! In my case, I just wanted feed my peripherals some data from external memory! What’s even worse was that there’s already a driver. Some might reasonably say that should be good a thing! I wouldn’t have to write, and then debug, my own driver. But, provided drivers or libraries often give me a reason to read even less of the device’s datasheet.
But, exactly what challenge did I run into? Well, when I first configured all the DMA through the provided Standalone driver, I got it to work, sort of! Of course, “sort of” really means it didn’t work, but it kind of worked! Specifically, the core would continuously run in a loop of repeating transfers for a long period of time and then stop. And since I was using the DMA’s Multi Channel mode, I knew from skimming the data sheet there’s no way the DMA can even run in its cyclic mode! I was stuck on this problem for a while, and even the DMA’s status registers couldn’t help me. It’s always a bummer when you know there’s an error, but the device you’re using says otherwise.
So I read the entire datasheet ( honestly, it was more I skimmed less ) and found the source of my problem. Because I was running the DMA in its Multi Channel mode, the DMA is configured for only 2D transfers. Basically, this meant I needed to set an extra parameter in each of the buffer descriptors associated with each transfer! Funny enough, I probably could gotten away with not reading ( or skimming a lot of ) the DMA’s datasheet if I had followed the right example. Oh well, I definitely learned to pay closer attention to details!
Who am I kidding? I just got better at skimming! Back to the rest of this project...
Referring to the block diagram, the Out Channel itself consists of three components. The first, called AWGN for Additive White Gaussian Noise, is the HLS-implementation of the Polar Box Muller algorithm discussed earlier. Since the implementation is small, I will show a snippet of it here.
... do { u1 = ( ( float ) lfsr() ) / ( ( float ) (1<<16) ); u2 = ( ( float ) lfsr() ) / ( ( float ) (1<<16) ); u1 = 2.0f * u1 - 1.0; u2 = 2.0f * u2 - 1.0; w = u1*u1 + u2*u2; } while ( w >= 1.0 ); w = sqrt( (-2.0 * log( w ) ) / w ); gs[ 0 ] = u1 * w * ( ( float ) *stdd ); gs[ 1 ] = u2 * w * ( ( float ) *stdd ); ...The algorithm generates two pseudo-random samples, which means that the algorithm only needs to be executed once every two input samples! The function "lfsr" refers to the Linear Feedback Shift Register ( LFSR ) implementation./* https://en.wikipedia.org/wiki/Linear-feedback_shift_register */ uint16_t lfsr() { static uint16_t cur = 0xACE1u; uint16_t bit; uint16_t ret = cur; /* taps: 16 14 13 11; feedback polynomial: x^16 + x^14 + x^13 + x^11 + 1 */ bit = ((cur >> 0) ^ (cur >> 2) ^ (cur >> 3) ^ (cur >> 5) ) & 1; cur = (cur >> 1) | (bit << 15); return ret; }Admittedly, my LFSR function is pretty much a modified version of the one found on Wikipedia. But, it does the job, which is to generate uni-formally distributed samples!The only problematic part of this implementation is the fact that the implementation is nondeterministic in terms of execution length, all due to the while-loop. This could be troublesome for a system that requires data before specific instances of time. Specifically, because this project is audio, the sound can potentially lag or distort if the algorithm runs for too long. The trigonometric form of the Box Muller algorithm is actually deterministic, but runs far slower and demands more resources. Would it have been sufficient? Actually, judging from the analysis the Xilinx HLS estimates, it would have barely passed in terms of latency.
Barely passing is VERY unsettling, however! Plus, I was worried about running out of DSP hard blocks. The polar implementation already eats up 34% of the FPGA’s total DSP resources alone. And, I’m guessing the trigonometric implementation would have at least doubled that percentage. In my experience with FPGAs, utilizing too much of a single resource leads to potential issues with routing, too.
The second of the three cores in the Out Channel is Prepare PWM. In spite of its name, this HLS-generated core doesn't actually generate the PWM signal that’s fed into the amplifier. The job of Prepare PWM is to simply convert the signed 16-bit output of the AWGN core to an unsigned 10-bit value.
The unsigned value is finally passed into the Speaker Controller, the third and last core of the Out Channel. Instead of HLS, this core needed to be developed in VHDL since it’s main job is to buffer samples in a FIFO, and output them at a consistent rate as PWM signals. Not sure if this is possible in HLS at this point, but it would be SUPER cool to have inline HDL, similar to inline assembly! Effectively, inline HDL would behave in a similar manner as assembly; for low-level needs, inline HDL could be used to implement hardware interfaces such as PWM or SPI, whereas the C/C++ code can still be used to take advantage of common but larger interfaces such as AXI!
Whelp, that’s it! :D
Anyone who’s interested in more specific details of the project can take a look at the Vivado 2016.2 project itself!
GitHub Repository: https://github.com/andrewandrepowell/scatter_dma
-
Zybo OpenCV Real-Time Video Processing
08/29/2016 at 02:00 • 0 comments -
Video Capture with Webcam
08/18/2016 at 21:41 • 0 comments -
OpenCV
08/17/2016 at 02:49 • 0 comments -
AXI Display Core driving VGA Interface!
08/12/2016 at 04:22 • 0 commentsPlease also check out the video another an a separate but related project! Finally got myself a microphone to connect to the Zybo's audio codec, and as an added bonus, started to use High Level Synthesis for the first
-
I2C Device Driver with LCD!
08/12/2016 at 04:17 • 0 comments -
GPIO SysFs!
08/12/2016 at 04:16 • 0 comments
Embedded Software Systems!
Collection of small hardware and/or software projects not worthy enough for dedicated project pages, but interesting enough to share!
 andrew.powell
andrew.powell A small difference between this log and the last is that there's a capacity associated with each arc in the network, instead of a single capacity associated with every arc. Now, the commodities are once again defined as the following.
A small difference between this log and the last is that there's a capacity associated with each arc in the network, instead of a single capacity associated with every arc. Now, the commodities are once again defined as the following.