This log documents three questions: what, why and how in tool path planning.
Note that if you are not clear the 3D printing terminology used in the log, please refer to glossary here.
What
Most of the time the "what" is more important than the rest of questions. In fact, it took me quite some time to ask the right/good question in tool path optimization. This is due to the fact that my understanding of slicing algorithm started from zero on May 4th 2018.
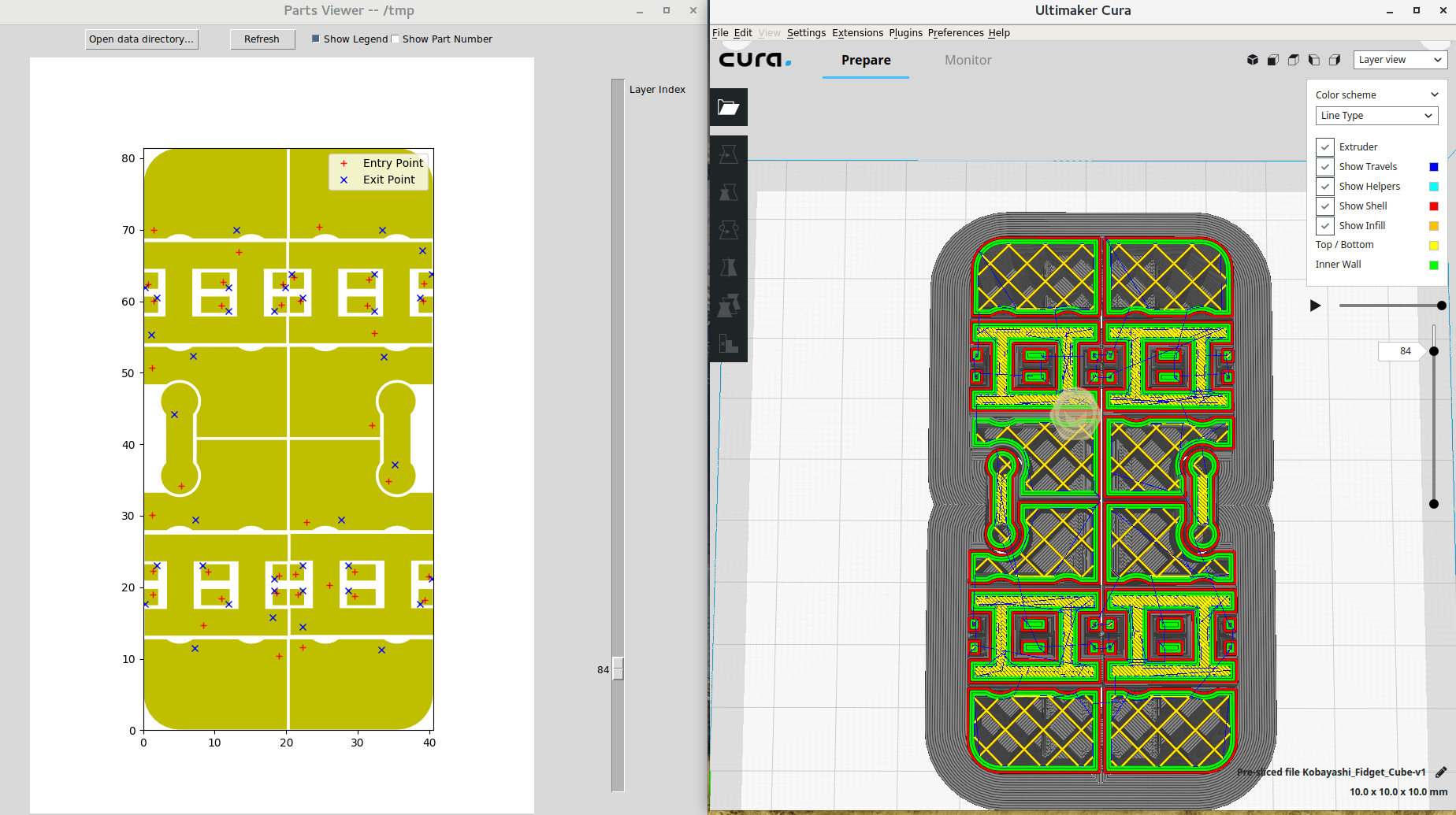
Slicing engine for FDM printing is quite new. There are tons of room for further improvement. My project focus point is tool path optimization for parts (a.k.a islands). A part is a closed polygon that have no overlap with another closed polygons in the 2D layer. See photo below is the 84th layer of a popular STL model fidget cube. The parts includes insets, infills and top/bottom layers (I hate using term but I have to, please check the glossary).
Each part has their an entry point and an exit point. In slicer, you can change the printing order of insets and infills. Thus, change its entry point, exit point and part order. But god knows how they figure out the entry point of each part. I'm pretty sure they are sub par choice for the most of the time.
But for the time being. Let's solve one problem at at time. My problem statement is that find the optimized part travel order so that air travel distance is minimal.
Why
The 'what' in previous section seems to be easy to understand. But again, I want to tell you that it is the most difficult question. No kidding.
To answer why is easy. Because life is short. If you can save average 10 seconds in each layer by path optimization and there are 200 layers in slicing, do your math you will be amazed how many minutes you can save due to optimizer.
In addition, the print quality may improve as well. Because less air time travel means less retraction and less messy stringy...
How
In theory, this is an asymmetric travelling salesman problem. Every computer science kid will tell you this is NPC problem in their complexity text book. In English term, it is a problem that can't be solved by a Turing computer easily.
In reality, we can SOLVE TSP with reasonable size easily. Up to 2018 -- operation research scientists have made a tremendous progress in designing and implementing mixed integer linear programming solver. In addition, improvement in beefy computation hardware also help solve the problem which was impossible to solve in the past.
I personally do a test in the best TSP solver in human history called Concorde. It can solve a complete graph with 1000 vertexes withing 5 seconds on my Intel Sandy Bridge i7 box.
So far I have output parts data and entry point and exit point of part into text file. The next step is to design and implement a solver.
 Ricky Zhang
Ricky Zhang
Discussions
Become a Hackaday.io Member
Create an account to leave a comment. Already have an account? Log In.