Making Sense of the Hall Sense

To generate a steady B-field for our experiment, we have two options to choose from:

1. Permanent Magnets
2. Electromagnets

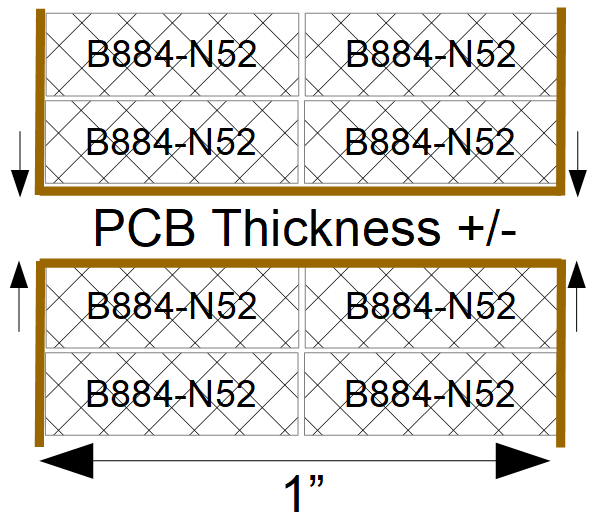
Before I choose a path, I'd like to do a quick study to determine the cost of building a magnet with a 1 Tesla flux density through a 1" x 1" area.  If more than 1 Tesla is needed, we can approximate the cost as a linear function of flux density.

Using Permanent Magnets:

Benefits of using permanent magnets are:

1. Different sizes, shapes, and strengths readily available
2. Stacking smaller magnets is equivalent to a single magnet of the same thickness
   1. Flux density (B) dependent on the magnet's dimension in the direction of the magnetic field's axis
3. Setup would require a simple mounting fixture

Some cons:

1. If using multiple small magnets, the B-field will not be uniform in certain places (compared to a larger permanent magnet or electromagnet) due to the gaps between the magnets.  (Not a show stopper)
2. Can get expensive as the number of magnets needed is increased to increase the B-field.

Example Jig set up:

• Using the B884-N52 rectangular magnets stacked in two rows, we can get a B-Field of ~ 1 Tesla (0.99 Tesla)
• Total cost would be ~$30.  The jig would be made from scrap wood I have laying around.

Analysis using an electromagnet coming in the next log...

Added the Hall voltage calculator.  Right now I only have copper in there, but feel free to use.  The process will be the same for different materials, just plug in the correct values.  

There are going to be some differences between my experiment and the original:

1. use copper, or some other metal clad board/insulator (price is king) for the hall element, not gold leaf
2. use copper wires, not brass because why brass when there is plenty of copper wire in my lab stock?
3. wires will be soldered directly to the element which should provide less terminal resistance than using highly polished brass contacts 
4. use an electro-magnet to generate the B-field with a split-core to place the hall element where the magnet shall have: a) a high permeability core, and b) a small split in the core as thick as the hall element +/- 2mm to minimize reluctance (and loss of flux) in the magnetic
5. use a better power source, Brunsen cells are somewhat out-of-date
6. to measure the hall voltage, I'll potentially need a high-precision amplifier and a current sense resistor to make my own galvanometer.

For the Hall element, I'd like to use either 1 oz or 0.5 oz copper clad board since minimizing thickness is key.  In Hall's paper, he stated that even using a strip of copper that 9cm x 2cm x 250um (that's micrometers, 10-6  meters) would fail to yield a detectable transverse voltage.  However, this could have been due to the limitations of the equipment he was using at the time.  

I'll  have to do some more research as to the reason for this, but it may still be worth a shot to try the 1oz or 0.5oz copper since their thickness is significantly less than 250um, 30um down to ~17um respective to the copper clad weight.

Doing some more research, I found that I'm basically re-creating the 1879 E. Hall experiment.  It's a very interesting read, and relatively easy one too due to it being written in the first-person narrative.  Papers these days are so dry and boring :).    

Hall stated the strength of the magnetic field he used was 20,000 times the strength of the "horizontal intensity of the earth's magnetism."  According to Wikipedia, Earth's magnetic field at the surface ranges from 25 to 65 microTeslas.  So let's see what it would take to generate 0.5 to 1.3 Tesla.

Another thing to notice about the original Hall experiment is the magnitude of input current that was put through the gold leaf.  From the looks of the data, the current put through the gold leaf was less than 100mA.  The test data Hall had collected did not have clearly defined units in the table, see below:

Hall goes on to postulate that the E-field generated is related to the momentum of the charge carriers (mass x velocity of charge carriers), with the velocity of electrons being equivocated to "C/s."  However, "C/s" in his paper means the ratio of input current to cross-sectional area of the hall element (which is actually current density).